拿什么喜欢你,物理?
《学习高中物理会有哪些坑?》连载文章将会分享一些学习高中物理时所面临的典型问题与困惑。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。





为什么要学物理?学物理有什么用?
《学习高中物理会有哪些坑?》连载文章将会分享一些学习高中物理时所面临的典型问题与困惑。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。


时间管理不是要纠结会不会浪费时间,而是在有限的时间里把事情高效地做完

人都会趋利避害的,一朝被蛇咬十年怕井绳

兴趣就应该保证它的纯粹性,一旦把兴趣变成了职业,你就得承担这条路上的各种压力

扔书一时爽,一直扔一直爽!只不过要是不能顺利毕业,扔多少就得捡多少
整体法适用这种情形吗
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。


问:若把两根导体棒看成系统,能否把它们受到的安培力看做内力(因为安培力等大反向)呢?如果可以的话,能否用整体法来分析这个系统呢?

静电计为什么可以反映电容器两极板间的电压
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。

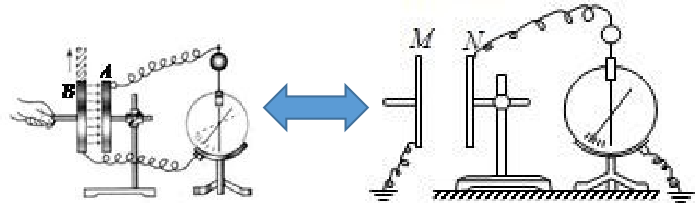
问:如图,静电计的这种接法为什么可以反映出电容器两极板间的电压呢?为什么不直接用电压表去测量电容器两极板间的电压呢?

再来看两者的使用方法。验电器在使用的时候,只需把带电物体靠着验电器的金属球上即可。但是静电计在使用的时候,必须把金属外壳接地,而金属球与电容器的某一极板相连(此时,电容器的另一极板接地)。这种接法等同于金属球与电容器某一极板相连,而金属外壳与电容器的另一极板相连。

当充好电的平行板电容器与静电计相连后,平行板电容器就会给静电计充电!(谁让静电计也是个电容器呢!)但是静电计的电容是很小的(可以借用平行板电容器电容的决定式来定性判断),所以静电计从平行板电容器那里获得的电荷是很少的,相对于平行板电容器来说可以忽略不计;但是对于静电计来说,这就足够它的金属片张开了。显然,静电计所带的电荷量越多,张角就越大,对应的就是静电计的金属杆与金属外壳间的电压越大——即平行板电容器的极板电压越大!如此一来,静电计金属片的张角大小就能反映出与之并联的电容器极板间的电压大小。
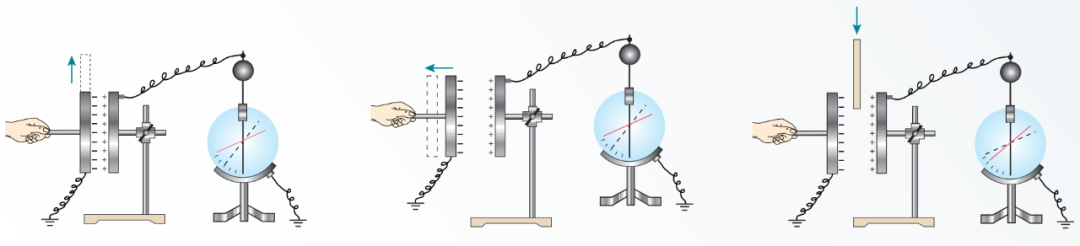
不过说到测量电容器两极板间的电压,怎么能冷落正当名分的电压表呢?这得从上述实验的目的和电压表的构造说起。上述实验是想探索平行板电容器的电容大小会与哪些因素有关,所以必须得让电容器始终带电且保证其带电量不变,通过观察极板间的电压变化,根据
而电压表是何等人物?它是一个通入电流就能反应自身两端电压大小的定值电阻,和一根导线的区别就是它的电阻很大而已。正是这个特点,此实验里的电容器就会拒绝和它握手——一旦你把电压表和充好电的电容器两极板相连,极板上的电荷马上就中和了,也就是放电了!即使后面再怎么改变电容器的构造,电压表的指针都会乖乖停在零刻度!实验也就探究了个寂寞......
收起阅读 »一文看懂测量的误差与估读
一、误差
把测量值与被测对象的真实值的差值称为测量的误差。
这就是一个典型的随机误差的例子
二、算术平均值靠谱?
想必大家都知道对同一对象多次测量取其算术平均值就能很好的减小随机误差。不过在历史上这个观念可曾备受质疑,为啥呢?这得从误差的认识说起。

这就从数学上证明了对多次测量结果取算术平均值的效果要好。
是不是想起了被描点作图支配的恐惧?
三、怎么估读呢?
且读数的最后一位要与仪器误差
刻度尺

螺旋测微器
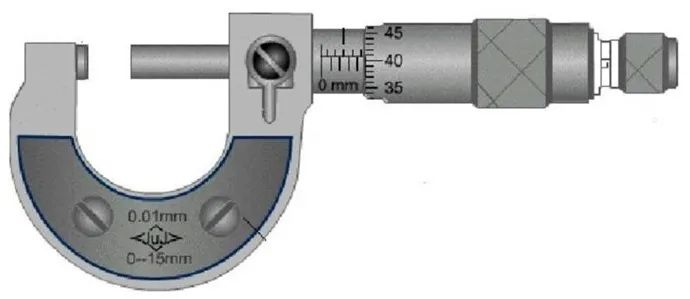
螺旋部分的最小分度是0.01mm。按照‘半格误差’来算,则仪器误差为0.005mm,所以仪器误差出现的位置为0.001mm。显然它也是十分法估读。读数的结果就是小数后面取三位(以mm为单位)。比如2.225mm,5.640mm。最后一位小数都是估读的,也是有效的。
弹簧秤

这个弹簧秤的最小分度是0.05N。按照‘半格误差’来算,则仪器误差为0.025N,由于误差值只取一位有效数字,所以仪器误差出现的位置为0.01N。由于误差位数为最小分度的五分之一,故称为五分法估读。读数的结果就是小数后面取两位(以N为单位)。比如0.32N,1.15N。最后一位小数都是估读的,也是有效的。
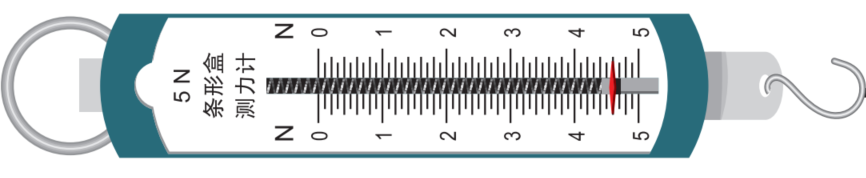
这个弹簧秤的最小分度是0.1N。按照‘半格误差’来算,则仪器误差为0.05N,所以仪器误差出现的位置为0.01N。这种情况下是十分法估读。读数的结果就是小数后面取两位(以N为单位)。比如0.32N,1.15N。最后一位小数都是估读的,也是有效的。
电流表

电压表

多用电表欧姆档
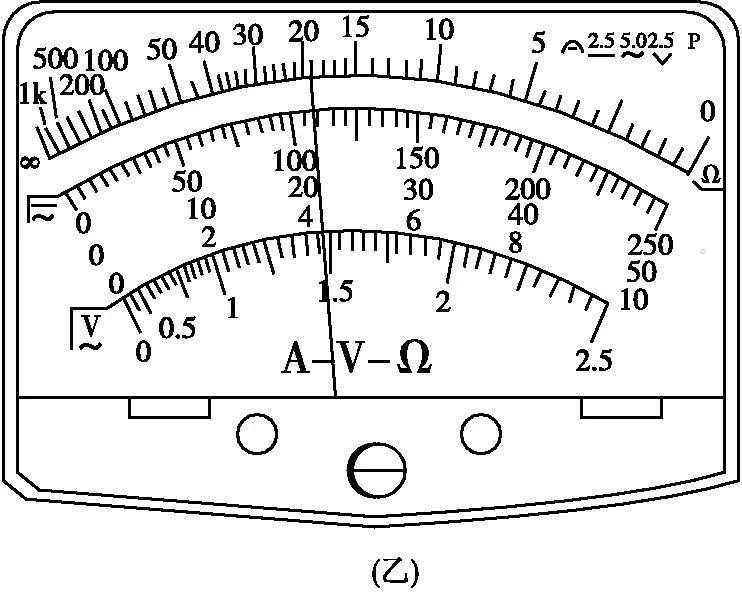
欧姆表(多用电表的欧姆档)的原理决定了其刻度是不均匀的,根据表盘刻度的分布特点,选择分段判断其仪器误差出现的位数,从而采取对于的估读办法。(该法同样参见文末给出的论文)
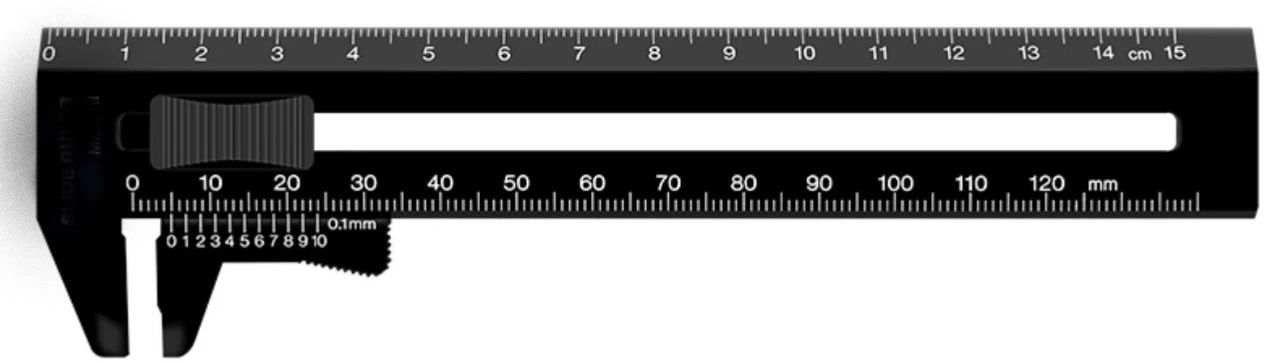


所以游标卡尺的估读采取就近读刻度的原则——哪怕游标尺上没有任何一条刻度与主尺刻度完全对齐,也应该选择游标尺上与主尺刻度靠得最近的那条刻度来读数。由于游标卡尺的读数规则是:主尺的准确读数+对齐条数*最小分度值,而对齐条数没有按照前面常见仪器那样估读,所以就造成了游标卡尺不需要估读的说法。
或许再经过若干年的发展,现有的学生实验仪器都会普及电子化,读数问题不再上得来台面,就像如今算盘的地位一样。但是对待准确实验数据的态度依旧是起码的物理素养,所以别去幻想可以逃避如何正确地读数哟。
[3]何志强,王笑君.从误差理论看中学常见测量仪器的估读[J].物理教师,2014,35.
收起阅读 »人踢足球,弹力对足球做不做功?
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。


显然这个形变就是脚对足球施加的弹力所造成的,而足球发生形变说明其与脚接触的部分在弹力作用下有位移呀!正是这个极短的过程,弹力对足球做了功,从而使得足球的动能发生了变化。
(1)我们依然可以根据功的定义下结论:弹力一定做了功,功的定义没毛病。
(2)在具体的问题里,一个假定的模型失效了,就会得出一个矛盾的结论。


为什么电场强度的大小与电势的高低没有关系?
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。

场强和电势都是描述电场特点的物理量,但是它俩之间的大小却没有相互关系。抛开电势的值有相对性的特点外,如果事先定好零势点,能不能说电势高的地方场强大,电势低的地方场强小呢?这是初学者很容易犯错的地方。


显然这两个量的大小确实没有半毛钱的关系呀。下山道路的陡峭程度难道取决于你所在的位置?要是普通群众想方便爬山,人们总会想法修建平缓的道路;要是探险爱好者来爬山,Ta们恨不得直接跳下去 。
。

高压输电到底是降低了输电线路上的电能损耗还是增加了损耗
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。


远距离输电的示意图
先别着急问题里的疑惑,咱用一组具体的数据算一算,直观体会一下高压输电带来的效益有多显著。



损失一下减少了400倍!相当于现在用汽车给你运粮食了,也就用点油而已,粮食给你管饱!这肉眼可见的效益提升,只能猛夸高压输电好,高压输电妙,高压输电呱呱叫!


欧姆定律为什么不适用于转动的电动机?
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。


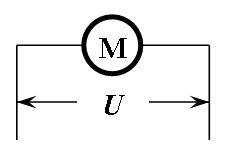
那么问题就来了,为啥电机转动的时候不适用欧姆定律呢?其实严格来说,应该是电机转动的时候,加在电机两端的电压
这得从电机的工作原理说起。电机内部除了线圈之外,另一块核心部件就是磁体。当电机通电后,其线圈中有电流,因此处于磁场中的通电线圈就会在安培力的作用下开始转动,这就是电机能转动的原因。
只是通常情况下,咱们并不知道电机的具体参数——比如线圈匝数、电机转速、电机内部的磁感应强度等, 因此没法算出电机转动时产生的反电动势大小。所以根据上面的等式没法算出通过电机的电流。至于怎么算,这个问题在教辅上不少见,咱就不啰嗦了。
倘若电机被卡死不转了,情况就变了。为啥?因为没有线圈的转动,哪来的反电动势呢?如此,通过电机的电流就变为了:
电机线圈其实和导线差不多,内阻能大到哪去呢?所以电机一旦被卡死(通电条件下),通过线圈的电流会显著增大,由此会带来显著的发热。来,电机张嘴,做个核酸检测......而电机正常转动时,由于线圈切割磁感线产生了反电动势,所以通过线圈的电流不是很大,电机也就能长时间正常运转啦。
总之,对于电机来说,无论其是否转动,欧姆定律肯定是适用的。只是当其转动时,加在线圈两端的电压要减掉其产生的反电动势而已。
洛伦兹力对运动电荷不做功,为啥安培力却可以对通电导线做功?
“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。

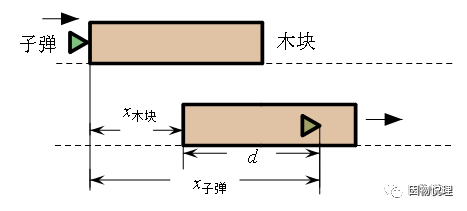
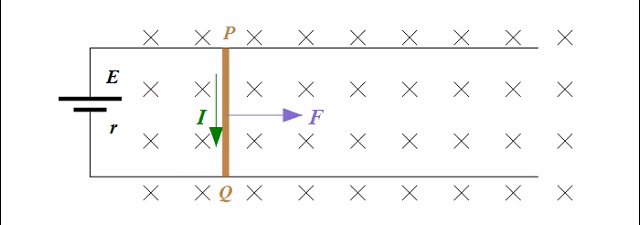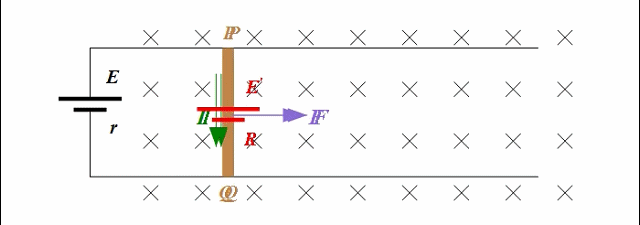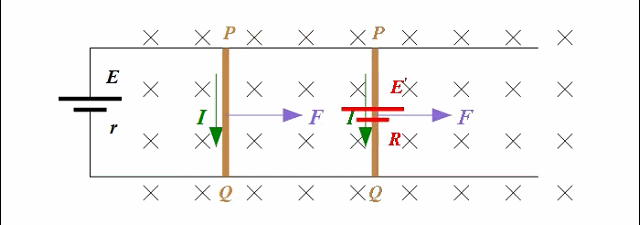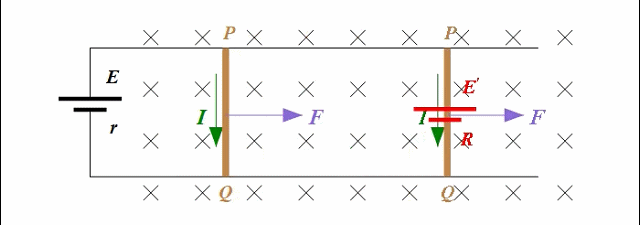
有图有真相,先来瞅瞅电源供电的情形吧。示意图如下,把一根导体棒接在一个电源两端形成闭合回路,导体棒处于磁场中,且磁场方向垂直于导体棒所在的平面。咱们只是想弄清上述问题,所以就弄一个正电荷q给代表那些自由电荷啦(用负电荷q一样,随你)。

构建合适的简化模型至关重要
在电源的鞭策下,这个正电荷q岂敢怠慢?那还不得屁颠屁颠地从a到b发生定向移动?如此,正电荷q也就有了定向移动的速度,或者说导体棒里就形成了电流。别忘了导体棒可是处在虎视眈眈的磁场中,那么对于正电荷q来说会受到洛伦兹力,而对于导体棒来说会受到安培力。各个物理量的方向如下图所示。

看到这里,禁不住大腿一拍!你瞅瞅,洛伦兹力果然要做功吧?!导体棒在安培力(洛伦兹力)的作用下会向右运动起来,显然安培力(洛伦兹力)对导体棒做了正功!

你若把正电荷q的运动看成两个运动的合成——从a端定向移动到b端、随棒水平向右移动,那么这两个分运动就会导致正电荷受到两个洛伦兹力,分别是图中的绿色箭头和黄色箭头。分开来说,这两个洛伦兹力分别对正电荷‘做正功’和‘做负功’。但是对于正电荷q来说,实际的速度是两个分速度的合成,其方向是斜向右下方的。因此正电荷q真正受到的洛伦兹力便是斜向右上方、且与合速度垂直的,这个真正的洛伦兹力也可以看成是图中所表出的两个洛伦兹力的合力。不用质疑,这个真正的洛伦兹力一定不会对电荷做功!!!
接下来就是熟悉的牛顿大法了。导体棒在安培力的作用下运动起来,经过一段短时间t后,棒的速度为:
这个分速度对应的洛伦兹力(上图中黄色箭头所表示的力)大小即为:
不要被这几个等式给唬住了哈,纯粹就是套公式化简而已,只要记得把速度和力对应好就行了。接下来就该算算各个分力的功啦,再次偷个懒,算功率就行了。显然安培力的功率为:
白纸黑字清楚地显示了这两个分量的功率一正一负、大小相等!这还有什么好说的呢?所以正电荷q真正受到的洛伦兹力肯定是没有对它做功的,而我们说安培力对导体棒做功,其实是洛伦兹力的一个分量在做功。但是洛伦兹力的另一个分量一定在做等量的、符号相反的功,只是我们没有关注而已。


导体棒在匀强磁场中以速度v切割磁感线运动,用导线把导体棒两端相连形成闭合回路。显然导体棒里会形成感应电流,导体棒会受到安培力。