统计物理的基本思想
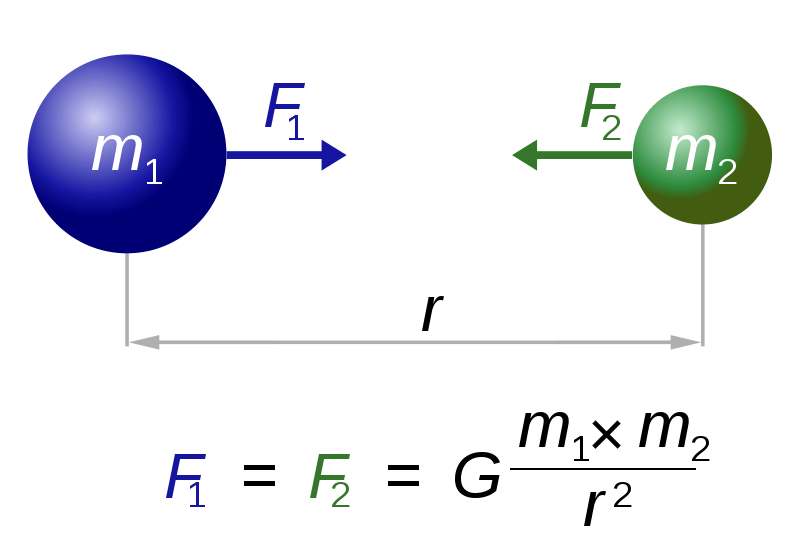
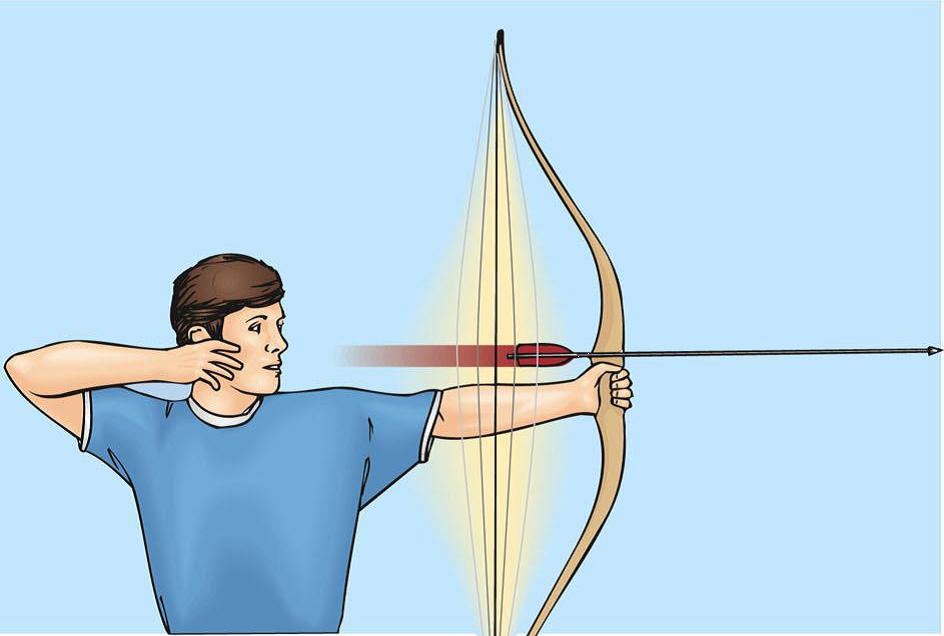
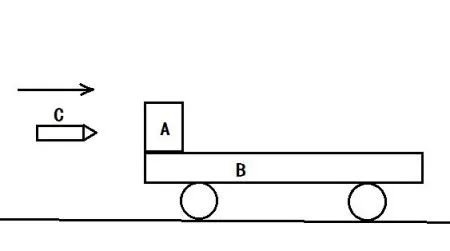
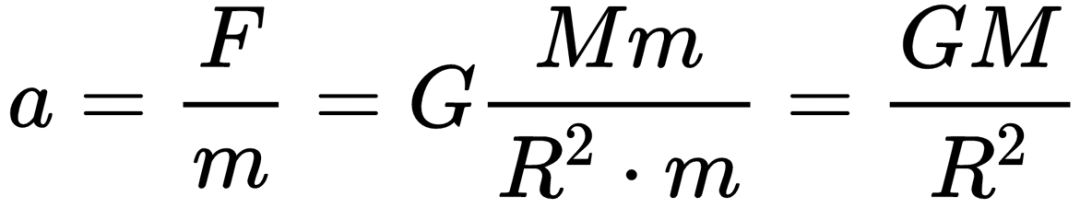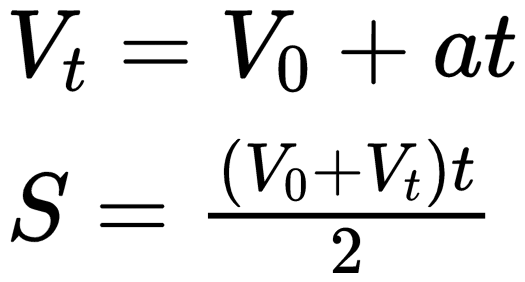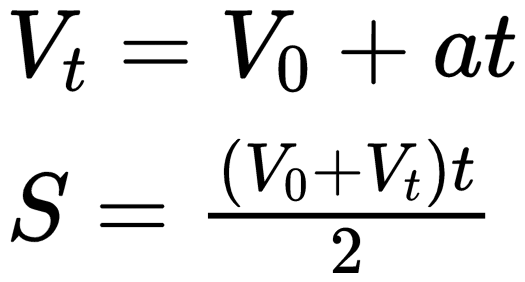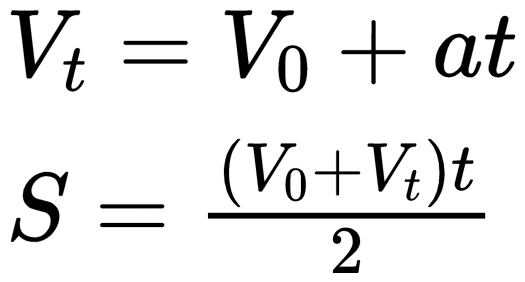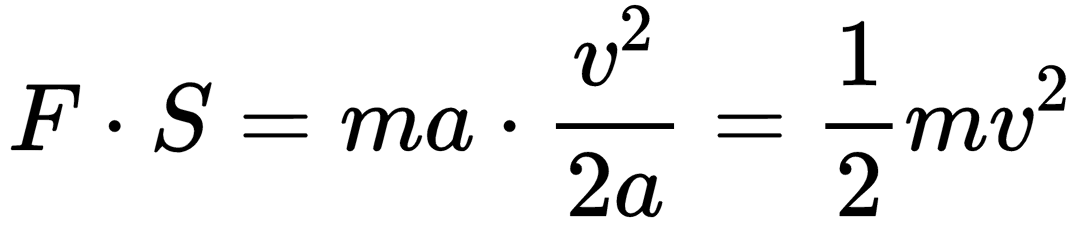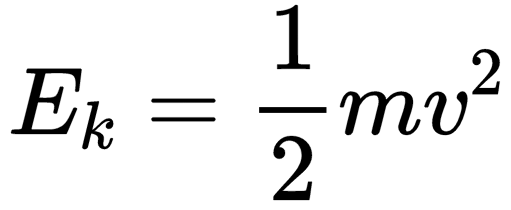统计物理的基本思想
作者 | yubr
1 基本概念和基本思想
统计物理的研究对象是大量微观粒子（mol级别，也就是 数量级）组成的宏观系统。统计物理的基本目标是从系统的微观性质出发，推导出系统的宏观性质。为此，我们先澄清几个概念。
我们假设一堆的气体分子（ 数量级）组成了一个系统。这个系统可以有自己的体积，压强，温度，内能等参数，这些参数称为系统的宏观量。另一方面，这 量级的分子每一个都可以有自己的位置矢量、速度矢量、动量、能量等参数，这些参数称为系统的微观量。
系统的微观量每时每刻都在不断变化，而系统的宏观量可以不随时间变化。我们把宏观量不随时间变化的系统称为处于平衡态的系统。
为了描述这个系统的状态，我们有两种方法。
第一种方法是用系统的一组宏观量来描述系统的状态：
系统的状态 =
上式表明，当系统的压强、体积、温度、内能等宏观量分别取一组特定值的时候，我们得到了系统的一个状态，这种用一组宏观量来标记的状态称为系统的宏观态。
第二种方法是用系统中每个粒子的微观量来描述系统的状态：
系统的状态 =
上式表明，当每一个粒子的速度和动量分别取一组特定值的时候，我们得到了系统的一个状态，这种用每一个粒子的微观量来标记的状态称为系统的微观态 。
从原则上讲，我们可以对每一个粒子做动力学分析，（对经典系统，每一个粒子都服从牛顿运动定律，对量子体系，每一个粒子都服从薛定谔方程，它们都是决定论性的动力学方程，只要初始条件和边界条件给定，系统以后的演化就可以唯一确定），联立 个微分方程，然后精确地确定任意时刻每个粒子的运动状态，这样我们也就确定了任意时刻系统的微观态。
当然，很遗憾，这种方法完全不具有可操作性，根本原因还是因为宏观系统包含的粒子数实在太多了，宇宙中没有（现在没有，以后也很可能不会有）任何一台超级计算机能在有限时间内联立求解 个方程 ，所以我们根本不可能通过求解出每一个粒子的微观量然后外推出系统的微观态。
暴力求解的方法不切实际，那么是不是就意味着我们就没法描述一个宏观系统的状态了呢？当然不是！这就是统计物理大显身手的时候了，我们必须注意到以下重要的事实：（1）实验上可以测量的只有系统的宏观态（系统的微观态不可测量），而确定系统的宏观态只需要几个有限的宏观量就行了；（2）一个宏观态可以对应大量不同的微观态，而且不同的宏观态对应的微观态的数目并不相同 。
接下来，我们来引入统计物理中最重要的假设（也是唯一需要的假设）：等概率假设
等概率假设：对一个处于平衡态的孤立系统，系统的每个微观态都有相同的可能性达到。
这是一个非常朴素和自然的假定，根据这个假定，再加上上面的分析，我们可以很自然地得到下面的推论：系统最有可能取到的宏观态是那个对应了最多微观态数的宏观态。
既然我们可以测量的只有系统的宏观态，而确定一个宏观态只需要几个有限的宏观量，那么为了描述一个宏观系统，我们只需要得到所有的宏观量的值就行了。对此，热力学采用了直接用实验测量来确定宏观量的方法，这是一种自下而上(bottom-up)的唯象方法；而统计物理则采用了从微观态出发，然后理论推导出宏观量的方法，这是一种自上而下(top-down)的理论方法。我们这里只讨论后者。
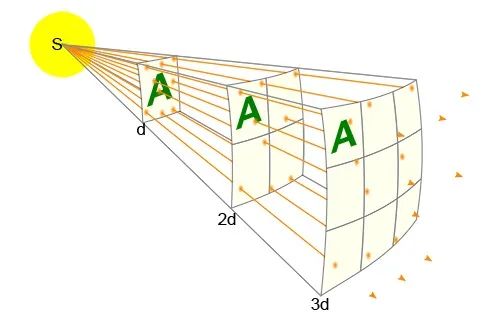
必须要注意的一点是，（可测量的）宏观量其实是（不可测量的）微观量统计平均后的结果。例如我们考虑一个装满气体分子的宏观容器的压强，我们测量到的压强并不是某一时刻某个分子撞击器壁的力，而是一段时间内大量分子撞击器壁后的平均效果。更一般地，设 是一个任意的物理量，则有
其中：
是一个相对宏观系统极小的时间尺度； 表示时刻系统的物理量 的值，这是一个微观量，并且每时每刻都在随着时间剧烈涨落，因而不可测量； 表示时刻我们测量到的系统的物理量 的值，这是一个宏观量，它其实是 这段时间内微观量 的统计平均，对于平衡态系统，它是个不随时间变化的量，可以测量。
但是，用上面这种“时间平均”的方法来计算宏观量其实并不可行，因为虽然 是一个相对宏观系统极小的时间尺度，但它相对微观世界极大。例如，我们还是考虑一个装满气体的宏观容器，在室温下，每秒内气体分子撞壁 次，每撞击一次，系统的微观状态就改变一次， 的值也可能改变一次。测量一秒内 个 的值然后取平均，这显然是不现实的。
为此，我们引入系综的概念。将系统复制 份， 是一个非常大的数字，并且保证这 个复制品的宏观态相同（即系统所有的宏观量都相同），但是微观态可以不同，这样的 个系统组成的集合就称为系综。引入系综的好处是可以把上面实际上不可操作的“时间平均”等价转化为下面可操作的“系综平均“：
时间平均的右边各项分别为不同时刻系统的微观量；系综平均的右边各项则为同一时刻系综中不同系统的微观量。各态历经假说 保证了时间平均和系综平均是等价的，这也是系综理论成立的基础。
设 时刻系统位于微观态 的概率为 （此时系统的物理量 取到的对应微观量记作 ），则上面的系综平均可以改写为
从下面开始我们将忽略尖括号右下角的“系综“两字，不加特殊说明，统计平均都默认是系综平均。
所以我们可以看到，整个统计物理的核心就是求解系统落在每个微观态i上的概率 。因为一旦有了，要求出任何物理量的宏观量（即我们实验测量到的量），我们只需要代入对应的微观量的值，然后按照上式做加权平均即可。求出了所有的宏观量，那么系统的宏观态也就完全确定了。这样我们就从系统的微观性质出发，推导出了系统的宏观性质，而这，正是统计物理的基本目标。
如果一个系统满足： ，则称系统处于平衡态，对应的统计称为平衡态统计； 如果一个系统满足：，则称系统处于非平衡态，对应的统计称为非平衡态统计；
我们下面只关注平衡态统计。
2. 经典统计
在统计物理中，我们常用的系综有三类：微正则系综，正则系综和巨正则系综，下面分别加以介绍 。
2.1 微正则系综（）
微正则系综是最简单的系综，它所包含的系统是孤立系统，且具有确定的粒子数 ，体积 ，能量 。设系统所有可能的微观态数为 ，则由等概率假设，系统取到每个微观态的概率为
因为系统的每个微观态都有确定的能量，即
所以系统的内能，即平均能量（宏观量）为
2.2 正则系综（）
正则系综包含的系统具有确定的粒子数 ，体积 ，温度 ，但是系统的能量 可以变化，我们的目标是求出正则系综中的系统取到某个具有特定能量的微观态的概率。
首先，为了保证系统具有确定的温度，我们可以把系统和一个大热源耦合，大热源的热容假设为无穷大，以至于其温度在热量交换下不变，所以当系统和大热源达到平衡态后，系统将具有和大热源相同的确定的温度，但因为系统存在涨落，所以系统的能量（微观量）并不确定，但是系统的平均能量（也即系统的内能，是宏观量）是确定的。
我们注意到系统和大热源整体构成一个孤立体系，它是微正则系综的元素，具有确定的能量 。设当系统能量为 时（此时大热源具有的能量为 ），系统具有的微观态数为 ，大热源具有的微观态数为 ，则系统和大热源组成的整体具有的总的微观态数为
显然这个数只和总能量 有关，并不依赖于 。因为这个系统和大热源的整体是一个孤立体系，所以我们可以使用等概率假设，这个整体取到每个微观态的概率 都相同
把此时系统所处的微观态标记为 （注意此时系统的能量为 ，大热源能量为 ），则此时系统和大热源整体可能取到的微观态数目为
所以系统取到微观态的概率为
因为热源很大，所以有 ，将上式两边取对数并且对 做小量展开，保留到一阶项，我们得到
联立热力学第一定律
和熵的统计定义
我们得到
所以
因为概率要归一化，所以我们最后得到正则系综中的系统处在微观态（对应能量为）的概率为
其中
称为系统的配分函数。上面的求和要包括系统所有的微观态。
有了系统处于任何微观态的概率，我们就可以利用配分函数计算出系统所有的宏观量的表达式，例如
内能
熵
亥姆霍兹自由能
系统的其他宏观量都可以由内能和亥姆霍兹自由能得到，例如压强 ， 熵 ，热容 ，等等。
2.3 巨正则系综（）
巨正则系综包含的系统具有确定的化学势 ，体积 ，温度 ，但是系统的粒子数 和能量 可以变化，我们的目标是求出巨正则系综中的系统取到某个具有特定粒子数和特定能量的微观态的概率 。
为了保证系统具有确定的化学势和温度，我们将系统和一个大粒子源与大热源耦合。利用和之前正则系综完全相同的分析方法，可以推出巨正则系综中系统处在微观态 （对应能量 ，粒子数 ）的概率为
其中 和正则系综中的温度定义一致，
称为系统的化学势，
称为系统的巨配分函数。
利用巨配分函数我们可以计算系统的任何宏观量，例如
粒子数
内能
熵
亥姆霍兹自由能
系统的其他宏观量都可以由粒子数、内能、亥姆霍兹自由能导出。
3. 量子统计
对于量子系统，我们不仅要作统计平均，还要作量子平均。具体来说，对任一物理量，
插入完备性关系，我们有
定义密度矩阵算符
从而
所以，量子统计的核心就是求出系统的密度矩阵 ，有了它，我们就能计算任何物理量的量子平均。
如果一个系统满足 ， ，则称系统处于纯态，此时密度矩阵 ；否则，称系统处于混合态。
从密度矩阵的定义出发，很容易证明如下的性质：
，等号当且仅当系统处于纯态时取到 的演化满足 von Neumann方程： ，其中为系统的哈密顿量
下面我们来推导在量子统计的框架下，正则系综和巨正则系综里物理量平均值（即可观测的宏观量）的表达式。
正则系综
概率
配分函数
密度矩阵
物理量的平均值:
巨正则系综
概率
巨配分函数
密度矩阵
物理量的平均值
附注
[1] 我们举一个形象的例子进行类比。考虑一个储蓄罐里放了100枚全同的硬币，盖上盖子用力摇晃均匀后打开，里面有的硬币正面朝上，有的硬币反面朝上。
所有硬币的状态的一种组合，例如“1号硬币正面朝上, 2号硬币反面朝上,..., 100号硬币反面朝上”，就是系统的一个微观态。显然，如果硬币全同，那么每个硬币都可以等可能地正面或反面朝上，所以每个微观态出现的概率都相同，等于 。
另一方面，你可以整体上数一数有多少枚硬币正面朝上，多少枚反面朝上，例如一种状态是 “43枚硬币正面朝上，57枚硬币反面朝上”，这就构成系统的一个宏观态。
[2] 为了有一个直观的感受，我们考虑1kg的氮气，这里面大概有个氮气分子。假如我们使用一台主频为3GHz的个人电脑进行计数，设一个周期可以数一个分子，那么这台电脑一秒可以数个分子，一年可以数个分子，数完1kg氮气中的全部分子需要整整2亿年！请注意，我们这里仅仅只是计数，如果要联立求解同样数目的微分方程组，那么还要花费多得多得多的时间。所以，可能直到宇宙毁灭的那天，你都没办法精确计算出1kg氮气中所有分子的运动状态。
[3] 还是考虑上面那个摇硬币的例子，我们可以看到不同的宏观态对应不同数目的微观态。例如：
"50枚硬币正面朝上，50枚硬币反面朝上"对应的微观态数为
"53枚硬币正面朝上，47枚硬币反面朝上"对应的微观态数为
"100枚硬币全部正面朝上"对应的微观态数为
如果每个微观态出现的概率都相等，那显然"50枚硬币正面朝上，50枚硬币反面朝上"这个宏观态出现的可能性最大，而"100枚硬币全部正面朝上"这个宏观态几乎不可能出现。
[4] 这种时间平均和系综平均的等价性由所谓的各态历经假说 (ergodic hypothesis) 来进行保证，该假说陈述如下：一个孤立系统，从任一微观态出发，经过足够长时间后，系统将遍历所有可能的微观态。这意味着，在时间 内（ 相对微观系统来说是一个足够大的时间尺度），系统能遍历所有可能的微观态；另一方面，只要系综中系统的个数 取得足够大，也能遍历所有可能的微观态，所以对时间作平均可以等价转化为对系综作平均。
[5] 对于宏观系统（粒子数 ），用不同系综处理得到的结果是一样的，因为不同系综处理结果的差别在 量级，当 时，，所以对宏观系统，可以根据问题的方便选择合适的系综进行处理。但是对于微观系统（粒子数 几十）， 相比 不可以忽略，所以不同系综处理的结果并不等价（例如涨落问题）。
[6] 注意，为微观量，即使当系统和热源达到平衡态后仍可以因为涨落而变化；而平均能量即内能是宏观量，当系统和热源达到平衡态后就确定不变了，也就是说总的宏观能量在系统和热源之间的分割在系统和热源达到平衡态时是确定的，这种分割方式将使得系统和热源整体具有最大的微观状态数，这也等价于热平衡时的两系统具有相同的温度。
[7] von Neumann方程在经典统计中的类比是Liouville方程： ，这里 为相空间的代表点密度（代表点密度和系统处于某个微观态的概率 是一回事），花括号代表Poisson括号。
[8] 下面第三个等号用了如下事实：任何厄密矩阵都可以按照其本征值和本征态分解，即
，其中 和 分别为厄密矩阵 的本征值和本征态。
熵是什么
熵是什么
作者 | yubr
本文想要用尽量通俗的语言介绍熵到底是什么。为了更加全面，我们将分别从熵的热力学定义，熵的统计力学定义（玻尔兹曼熵，吉布斯熵）和熵的信息学定义（香农熵，冯·诺依曼熵）来介绍，并揭示这些定义的相互联系。
1. 熵的热力学定义
利用卡诺热机和卡诺循环，我们可以证明如下的克劳修斯不等式，即对任一闭循环，我们有
等号当且仅当该过程是可逆过程时候成立。所以，对可逆过程
这告诉我们 的积分和路径无关，所以它是恰当微分，它的积分是一个态函数（所谓态函数，就是那些值只和状态有关而和怎么达到这个状态的路径无关的函数），我们把这个态函数就定义为熵
这就是熵的热力学定义。
联立克劳修斯不等式和熵的定义式，我们可以得到
等号当且仅当可逆过程可以取到。对于绝热系统， dQ=0 ，所以我们有
这正是热力学第二定律的一种等价表述，它告诉我们：对于绝热系统，熵永不减少。如果过程可逆，那么熵不变，如果过程不可逆，那么熵增加。
利用熵的定义，我们可以把热力学第一定律 改写为
2. 熵的统计力学定义
为了得到从熵的热力学定义得到熵的统计力学定义，我们先来考察温度的统计定义。
我们考虑两个相互之间可以传递热量的系统，但是它们整体和环境绝热。设两个系统的内能（即平均能量，是宏观量）分别为 和 ，随着两个系统之间的热量交换， 和 都会改变，但总能量 是一个常数，因为两个系统整体和环境绝热。设两个系统此时的微观状态数分别为 和 ，则此时整体的微观状态数为 。
这两个系统不停地发生能量交换，经过足够长的时间后，它们将达到热平衡，之后和将固定不变（再次强调，和 都是宏观量，是系统的平均能量，它们在系统达到平衡态后是不变的，但是因为涨落的存在，系统的瞬时能量（微观量）在达到平衡态后也可以不停地变化。关于宏观量和微观量的详细介绍，可以参看这篇文章：统计物理的基本思想。）
一个自然的问题是：当两个系统达到热平衡以后， 和 分别应该取什么值呢？或者说，平衡状态下，总能量 是怎么样在两个系统中进行分割的呢？
为此，我们先作出以下几个很合理的假设：
等概率假设：孤立系统所有可能的微观态有相同出现的可能性； 系统内部的动力学使得系统的微观态是连续变化的； 各态历经假设：经过足够长的时间，系统会遍历所有可能的微观态且经历每个态的时间相同。
根据这几个假设，我们得出以下结论：系统最有可能处于那个包含最多微观态数目的宏观态。对于一个大系统而言，“最有可能”将成为“压倒性的可能”。
所以，平衡态下总能量 在两个系统中的分割应该使得总微观态数 最大。
为了确定 ，我们只需要求解下式
用链式法则展开
因为 是常数，所以 ，所以
即
也就是说，上面这个等式对应了热平衡下两个系统的使得总微观态数目最大的那种能量分割方式，也就是热平衡下两个系统需要满足的条件。
根据热力学第零定律，处于热平衡的两个系统具有相同的温度，这和上面的等式是一致的，所以我们定义温度 为
上述定义温度的方式就是温度的统计定义，其中 是玻尔兹曼常数。这种定义方式和热力学中的绝对温度的定义是一致的。
有了温度的统计定义，将其与热力学第一定律
联立，我们就得到了熵的统计力学定义
这样，我们就从熵的热力学定义和温度的统计定义出发，推出了熵的统计力学定义。上式定义的熵称为玻尔兹曼熵（它刻在了玻尔兹曼的墓碑上），它告诉我们：一个系统的玻尔兹曼熵正比于这个系统的微观状态数的对数。所以玻尔兹曼熵是系统混乱度的衡量，系统的微观状态数越多，系统的玻尔兹曼熵就越大。
为了与信息学相联系，我们下面来推导熵的另一种统计力学定义。
假设一个系统含有 个等概率的微观态，则系统的总熵为 。但是，这 个微观态并不都是可以通过实验测量进行区分的，也就是说，它们对应的总熵并不全部可以测量。我们假设这些微观态被分成了几组，其中第 组包含了 个微观态，当然有 。
这些组是可以通过实验测量区分的，因为它们可能对应某一个宏观可测的性质，但是每个组内部的那些微观态是不可区分的。现在我们想知道对应可测量部分的熵的大小是多少？
因为第 个组包含了 个微观态，所以系统位于第 个组中的概率 ，第 个组中的熵为 ，因为每个组内部的微观态不可区分，所以 不可测量。
因为微观状态数具有可乘性，所以熵具有可加性（熵是微观状态数的对数），所以可测量部分的熵等于总熵减去不可测量部分的熵，不可测量部分的熵可以写为
所以可测量部分的熵等于
因为 ，所以最后我们得到可测量部分的熵的表达式为
上述熵的定义称为吉布斯熵，吉布斯熵的形式可以很容易和信息论联系起来，这点在下一节中将会看到。
3. 熵的信息学定义
这一节我们将尝试将信息量与前面介绍的熵联系起来，并给出熵的信息学定义。首先，我们考虑以下三句话：
牛顿的生日处在一年之中的特定一天； 牛顿的生日处在下半年； 牛顿的生日是某月的25日。
假如我们事先对牛顿的生日一无所知（事实上，牛顿出生于公元1643年元月4日），我们来看看这三句话提供的信息量和这三句话正确的概率之间的关系。第一句话正确的概率是百分之百，但这是一句废话，不能提供任何信息量，因为所有人的生日都是一年之中的特定一天；第二句话正确的概率是1/2，它能提供一定的信息量；第三句话正确的概率只有12/365，但是它能提供最大的信息量。所以我们看到，在缺乏任何先验信息的条件下，一句话正确的概率越大，则它提供的信息量越小。
在知道表述的信息量和表述正确的概率是反相关后，接下来我们来建立它们之间的定量关系。一个自然的假设是两个独立表述的信息量具有可加性，例如上面第二句话和上面第三句话提供的总信息量是它们各自提供的信息量之和；另一方面，两个独立表述正确的概率具有可乘性，例如上面第二句话和第三句话同时正确的概率为 ，是它们各自正确概率的乘积。信息量和概率的这种性质促使我们把信息量定义为概率的对数。
假设一个表述正确的概率是P，则这个表述包含的信息量Q定义为
这里 是一个正的常数，这保证了当正确概率上升时，信息量会下降。
上述这种信息量的定义是由香农 (Shannon) 给出的。如果我们取 ，并且选取自然常数为底 ，则这种定义将和热力学与统计物理中的结论一致；如果我们取 ，并且选取2为底 ，则此时信息量 的单位将用比特 (bit) 来量度。
假设我们有一组的表述，正确的概率分别为 ，信息量分别为 ，则我们把信息熵定义为平均信息量：
这种熵的定义称为香农熵。
我们来举一个简单的例子。设一个非均匀的骰子可以掷出6种结果，它们的概率分别为：1/10，1/10，1/10，1/10，1/10，1/2，则与每个结果相联系的信息量分别为 （取 ，并取2为底，则它们分别为3.32比特，3.32比特，3.32比特，3.32比特，3.32比特，1比特），香农熵为
取 ，并取2为底，则香农熵=2.16比特。
从形式上来看，香农熵（信息熵）和吉布斯熵（热力学熵）完全一样。并且，两种熵都衡量了系统的不确定度。一个系统的微观状态数越多，则混乱度越大，不确定度越大，系统的热力学熵就越大；类似的，一个表述正确的概率越低，它的不确定度就越大，从而它的信息量就越大，而香农熵对平均信息量进行了量化。所以，我们得出结论：热力学熵和信息熵本质上是一回事，它们都是对系统不确定度（混乱度）的衡量。这种热力学熵和信息熵的等价性，使得我们可以从信息论的观点着手理解热力学；同时，也意味着我们可以用热力学和统计力学中发展出来的工具去研究信息论。
最后，我们简单地介绍一下量子系统中的信息熵。上面的香农熵只适用于经典系统，对于量子系统，我们要如何定义信息熵呢？我们知道，经典统计中的核心问题是求系统处于某个微观态的概率，而量子统计中的核心问题则是求系统的密度矩阵，关于密度矩阵的详细讨论，可以参看：统计物理的基本思想。
设量子系统的密度矩阵为 ，则量子系统的信息量定义为
信息熵仍然定义为平均信息量
其中 为密度矩阵 的本征值。量子系统中熵的上述定义称为冯·诺依曼熵。
4. 总结
我们上面一共介绍了熵的五种等价定义：熵的热力学定义、玻尔兹曼熵、吉布斯熵、香农熵、冯·诺依曼熵，其中前三个定义属于热力学和统计物理的范畴，而后两个定义属于信息论的范畴。
但是我们上面证明了，热力学熵和信息熵本质上是一回事，它们都是对系统不确定度（混乱度）的衡量。这给我们展示了一个惊人的结果：本来看似毫不相干的热物理和信息论这两门学科，其实是可以通过熵来紧密相连的。
完美展示热物理和信息论联系的一个例子就是著名的麦克斯韦妖：擦除硬盘中信息的过程必然伴随着环境中热量的增加和环境中熵的增加。麦克斯韦妖的“微操”虽然可能使得系统的熵短时间内减少，但是当麦克斯韦妖的记忆容量被塞满时，它必须通过擦除记忆中的信息来重新储存新的信息，这种擦除信息的行为增加了环境的熵，这增量抵消了之前的微操所减少的系统的熵。所以整个宇宙的熵是不会减少的，热力学第二定律仍然成立。
伽利略逝世的那年牛顿诞生，真的是这样吗？
/ 伽利略逝世的那年牛顿诞生，真的是这样吗？ /
今天课代表就来和你捞一捞这老生不常谈的问题，以及这背后的原因。
2018 年霍金刚刚离世，吃瓜群众们就给安排上了——霍金 PK 杨振宁
且不说霍金和杨老谁更厉害，霍金的支持者指出霍金的生日是伽利略的祭日(1.18)，霍金的祭日是爱因斯坦的生日(3.14)，因此霍金是两位大佬的转世，当然更厉害一些。
哦，我的上帝！你们这帮可怜的家伙！你们这个理由简直糟糕透了，就像隔壁露西小姐做的香蕉派一样！
我们毫不怀疑从伽利略到牛顿的传承，牛顿持有的就是伽利略变换代表的绝对时空观，牛顿力学和伽利略的相对性原理配合的也是天衣无缝，似乎冥冥中俩人之间有着传承关系。
在这里我无意去抨击各种封建迷信的说法，我只是就伽利略死的那年牛顿出生了这件事情展开讨论。真的是这样吗？
先说结论：不是！
如果你上网查牛顿的生日，大概率你会查到两个版本，1642 年 12 月 25 日和 1643 年 1 月 4 日。然后你再去查伽利略逝世是在 1642 年，于是乎按照第一个版本的牛顿生日，就有了两位大佬同年交接的说法，而且圣诞节的特殊日子也给这种说法平添了些许神秘感。
这有啥好奇怪的，连我没怎么念过书的奶奶都知道，人就是有俩生日啊，一个阳历一个农历。不光有俩生日，还有俩岁数呢，一个周岁一个虚岁。
CASE CLOSED!
牛爵爷诞于 1643 年 1 月 4 日，农历任午(1642)年腊月二十五，属马，小生日。
你可能会觉得好笑，人家外国人又不过农历。没错，但仔细一想，两个生日确实可能是由两种不同的历法造成的，只是和我们的农历没啥关系。
所以回到刚才的问题，牛顿的两个生日分别来自两种不同的历法 —— 儒略历(Julian) & 格里高利历(Gregorian)。按照儒略历，牛顿生于 1642 年 12 月 25 日，而按照格里高利历（即我们今天所使用的公历），牛顿则生于 1643 年 1 月 4 日。
CASE CLOSED AGAIN!
刚才我们所说的伽利略卒于 1642 年用的是格里高利历，换算成儒略历是 1641 年。
所以无论按照哪种历法，说伽利略去世和牛顿出生在同一年发生的说法是错误的。而且，准确的说牛顿在伽利略死后几乎一年（361 天）后才出生的。
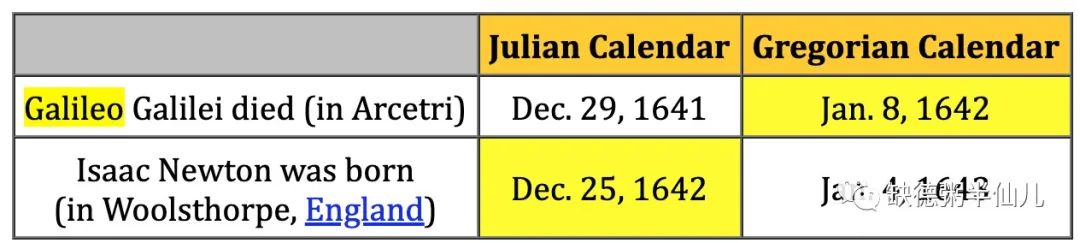
切勿将将两个黄格子拿来比较
很多牛顿粉丝会在圣诞节当天在社交媒体上发文为牛爷庆生，比如美国天体物理学家 Neil Tyson 就在 2014 年圣诞节发推给牛爷庆生
评论区有另一种声音：若不加声明，则我们默认的语境是格里高利历，你应该 1 月 4 日发推才对。
真的是这样吗？这背后有没有更深层次的原因呢？
我们随便 google 一下，就会发现两种声音都有
究竟我们该在哪天给爵爷祝寿呢？
还有一个很难被意识到的问题，为什么我们在查牛顿生日的时候会有俩，而查伽利略祭日的时候就只有一个？
要回答上述问题，就需要我们将时间拨回到很久之前，来深入了解一下这该死的混乱历法。
1 计时
要搞清楚历法，先得从计时开始。时间的流逝一直是人类所关注的问题，比如啥时候吃饭啥时候睡眠，比如季节对迁徙和农业的重要性，因此人们很早就知道了计时的重要性和必要性。
古代人们最直观的感受就是气候变化和昼夜交替，人们发现这两种现象貌似和天空中最显眼的两个天体——太阳和月亮——的运行规律有关系。
人们观察到了三个自然周期：
https://knb.im/mp" style="margin-top: 0px; margin-left: 0px; padding-left: 2.2em; outline: 0px; max-width: 100%; font-size: 15px; letter-spacing: 0.544px; text-align: justify; background-color: rgb(255, 255, 255); width: 515.844px; color: rgb(77, 124, 207); line-height: 25.6px; font-family: PingfangSC-LIGHT, sans-serif; overflow-wrap: break-word !important;">https://knb.im/mp" style="margin: 5px; outline: 0px; max-width: 100%; clear: both; min-height: 1em; white-space: pre-wrap; overflow-wrap: break-word !important;">1、太阳带来的四季变换
https://knb.im/mp" style="margin: 5px; outline: 0px; max-width: 100%; clear: both; min-height: 1em; white-space: pre-wrap; overflow-wrap: break-word !important;">2、太阳东升西落带来的昼夜交替
https://knb.im/mp" style="margin: 5px; outline: 0px; max-width: 100%; clear: both; min-height: 1em; white-space: pre-wrap; overflow-wrap: break-word !important;">3、月亮的阴晴圆缺
这正是老天爷赏的计时方法啊！
人们发现每隔一段时间，月亮进行一次周期往复（历经一个完整月相），这段时间就记为一个月（Month 显然来自于 Moon），目睹了新月的出现就开始一个新的月，这一天在我国叫做初一。
人们发现太阳东升西落很有规律，昼夜交替的周期貌似也可以用来计时，于是人们把太阳相邻两次燃烧的这段时间（日出到日出）叫做一天（day 一词来源于原始印欧语的燃烧一词），也有一些文明将日落到日落这段时间叫做一天。
然后人们慢慢发现这样一天的长度会变来变去的，因为每天日出和日落的时间会变的。冬天白天短，夏天白天长；而且我们现在还知道，日出和日落时间还取决于纬度，不同纬度地区的人感受到的一天的长短是不一样的。
而日出日落的中点也就是正午则比较有规律，相邻的间隔很稳定。而正午又有个特点就是太阳的位置最高，借助日晷这种神奇的道具，人们可以很方便的判断太阳的位置变化，很轻易就可以知道什么时候太阳最高（影子最短）。虽然每天正午是影子长短也是不一样的，但是在一个昼夜范围内，总会有一个影子最短的时刻。
于是人们改良了天的计算方式，把太阳位置最高到最高这段时间当做一天，这也就是我们现在所说的太阳日(solar day)，这就很巴适了。
人们还发现了季节和气候的交替，而且这个规律和太阳在天空中运行规律可以拟合，太阳在天空中运行回到同一个位置的这段时间差不多就经历一个春夏秋冬，体现在日晷上就是正午时长度变化的一个周期。
于是人们把这段时间叫做一年（year 一词来自于古语表示季节的词汇），我们现在把这叫做一个回归年(tropical year)，大概是 265.24xxx 天。
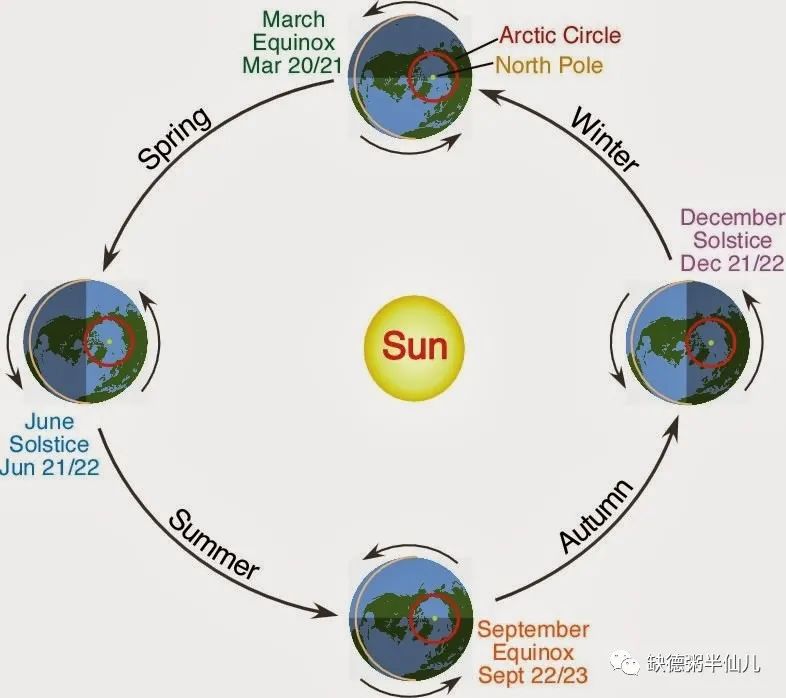
据记载，早在古埃及已经有了年的概念，而且古埃及人已经搞清楚了一年有大概 365 天，这很了不起。
细心的朋友会发现，计时单位除了年月日，还有一个很重要的，就是周，周的概念确实很重要，后文会看到这一点。
古巴比伦的苏美尔人开始有了“7天为一周”的雏形，源于他们发现的 7 天的星象意义。后来这种想法被犹太人发扬光大，犹太教的《圣经旧约》第一章开篇就提到上帝 6 天造万物、第 7 天休息（安息日）。慢慢地人们把 7 天定为一周。
2 历法
对于天文学还不是很发达古代人，显然月亮更好观测一些，月亮周期短，且月相区别明显。而且人们也更喜欢晚上吃完饭没事干的时候仰望头顶的星空。
于是人们开始用月亮来计时，并把这一套计时系统称为历法（calandar），calendar 一词最初源于古罗马的单词 calare（庄严地宣布，呼唤），表示古罗马的天文学祭司呼唤新月的到来，并庄严的宣布新的月份。此后的几个世纪里，罗马人把每个新月的第一天称为 Kalends（也来自于 calare），类似于我国的初一。
所以几乎所有文明早期都是按照月亮的运行规律创造历法，也就是我们说的阴历(lunar calendar)。比如两河文明、伊斯兰文明和古希腊等。
但是人们很快发现了阴历不太好用，原因是多方面的，最主要的两个原因是
1、它无法指导农业。民以食为天，对农民来说，种粮食最重要，种粮食受气候变化影响很大，但是阴历并不能反映出气候变化来，因为我们知道气候变化、四季交替等现象都是太阳带来的。
2、阴历有个致命的缺点，就是如果新月的时候赶上阴天或者雾霾，那么人们是看不到新月的，于是就会继续旧的月份，直到看见下一个新月才会开始新的月份。
所以逐渐的这些地区的人开始拥抱太阳，按照太阳运行规律创建了历法，叫做阳历(solar calendar)。
3 阴阳结合
书接上文，在全世界范围从大尺度上看，各文明历法始于月亮主导的阴历，然后人们发现阳历真香啊，就慢慢向阳历靠拢。
然鹅，使用阳历的人们逐渐发现一天和一年差距太大，以至于当老爹教儿子种地时告诉儿子你要在一年的第 100～120 天这段时间收庄稼，儿子还得一天一天数，很不方便。
于是人们就想要在天和年之间再来一个新的时间过渡单位。正好阴历的月满足这个条件。但是一个月 29 or 30 天，而一年有 365 天，介于 12-13 个月之间，很不整齐，阴历和阳历对不上。
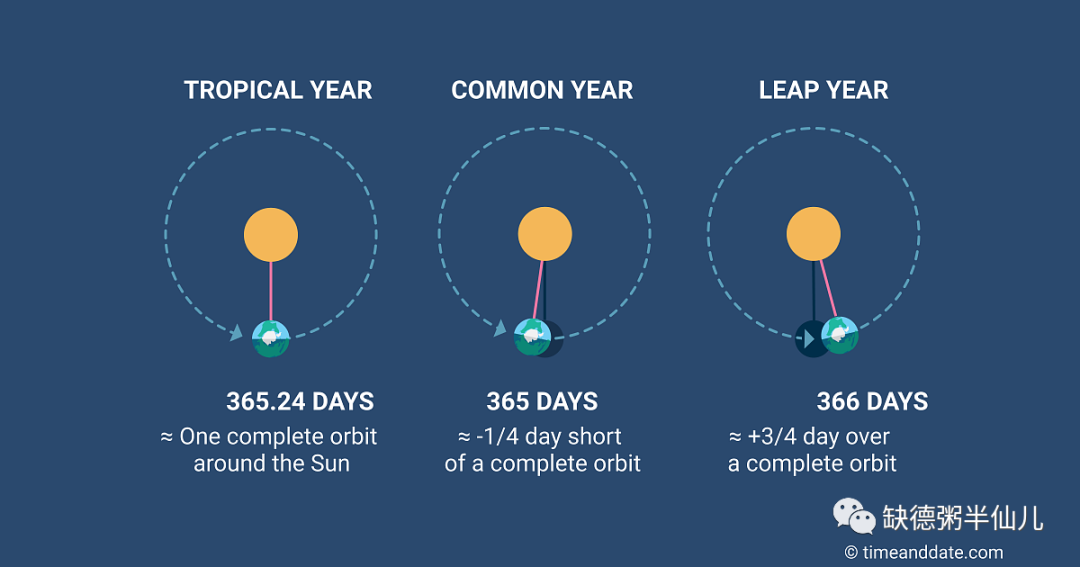
很多文明就遇到这个棘手的问题，大家的做法是先让一年有 12 个月再说，但是如果照搬阴历月，那么12 个阴历月通常就只有 345 天，剩下还差 11 天。
但是这 11 天怎么补，每个地方的人就不一样了。无外乎就两种方法，一是修修补补、二是推倒重建。要么在阴历月的基础上修正、要么破旧立新削足适履。
修修补补的典型代表就是古代中国 & 古巴比伦 颁布了汉莫拉比法典，刻在黑色的玄武……
两个国家都是在阴历的基础上，试图补上差的天数，来向阳历靠拢。但是补的方法不一样。
拿我国古代举例子，我们的做法每隔几年加一个闰月，只要长期平均下来大差不差就可以了。就这样我们将阴历和阳历两者结合，强行通过闰月的方法让阴历向阳历爸爸靠拢，毕竟人家有 24 节气这么牛叉的存在。
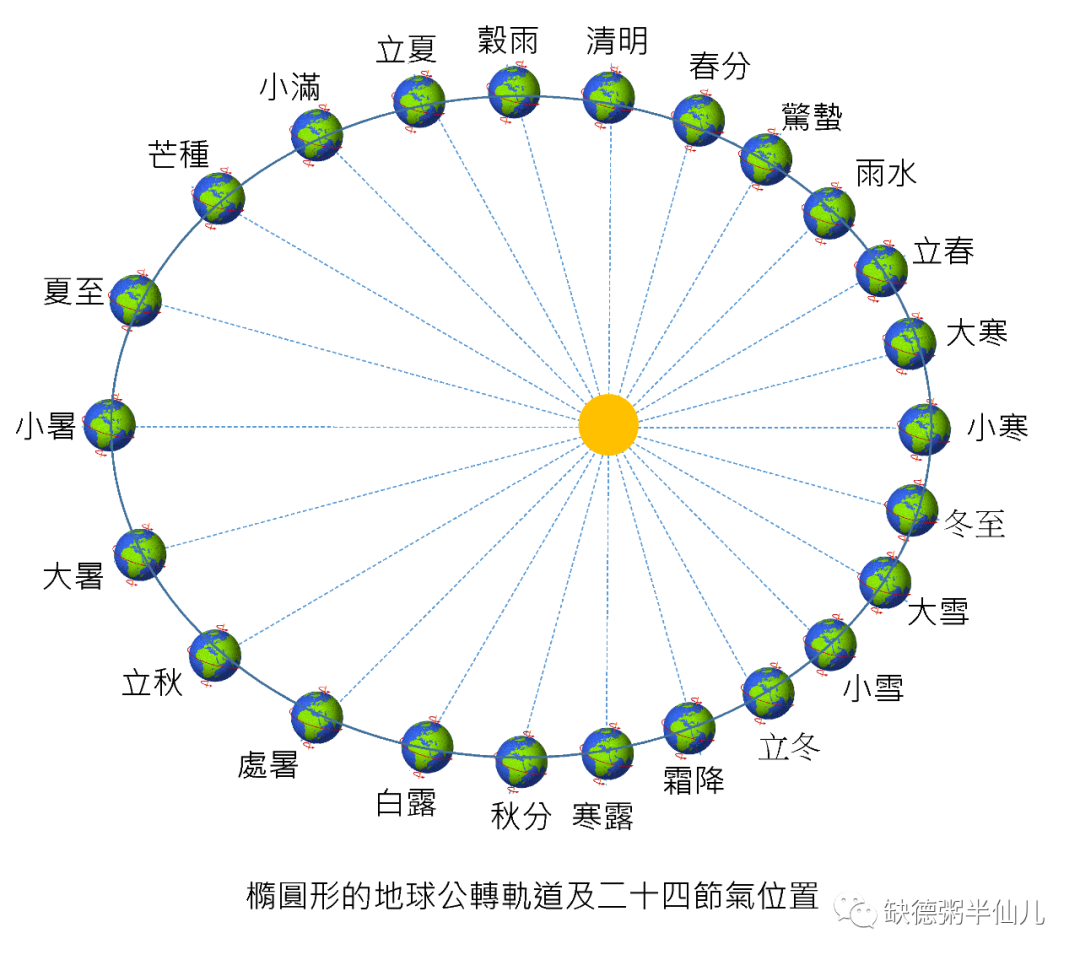
具体采取的方法是“19 年 7 润”法，即每 19 年（一个周期）内加 7 个（闰）月，同时保证让每个阴历月必须包含两个节气（准确的说是一个节气一个中气）。如果某个月比如六月只包含了一个节气，那么就再加一个润六月。
（1984年闰十月出生的朋友，到现在还没过第二个农历生日……）
这样便形成了我们现在的农历。农历是通过阴历和阳历结合而生的，所以是一种阴阳历(Lunisolar calendar)。生活中，许多老百姓口中总说阳历和阴历，他们将农历误称为阴历，这其是不对的。我国现行的两种历法准确的说是公历和农历。
感谢农历爸爸让我们每年多了好多假期，没有农历就没有春节、端午、中秋等法定节假日。
而古巴比伦的做法是 8 年 3 闰，国王会在一个 8 年内自行决定增加 3 个月，来向阳历靠拢。
破旧立新直接上阳历的文明最典型的就是古埃及。
由于埃及的地理位置离近赤道，因此四季不分明，气候变化小。从这个角度讲阳历用处也不大。
人家埃及逐阳弃阴也不是因为农业对气候变化的依赖。
那到底是什么原因让埃及官方嫌弃阴历呢？因为阴历无法预测一件对他们的农业来说最重要的事情——尼罗河的泛滥。
聪明的埃及人盯上了夜空中最亮的星——天狼星，他们发现天狼星在日出前与太阳在同一地方升起（偕日升）的这一天很特别，这一天总是发生在尼罗河泛洪的那几天。于是埃及官方就规定尼罗河泛滥和天狼星偕日升同时发生的那一天作为新年伊始。直接抛弃了阴历，强行自己定义了新的月。你不是要 365 天嘛，那我就简单粗暴点，令一年 12 个月，每月 30 天，再加上 5 天分配给 5 个神。
这样埃及版本的阳历就诞生了，埃及也是第一个使用阳历的文明。（准确的说，埃及使用的是天狼星历，一天狼星年和一太阳年之间差着大概几分钟这个数量级）
但是这样一年固定为 365 天，而一个回归年的时间要比 365 天多一丢丢，所以时间长了历法就会偏离太阳运行轨迹，4 年就会偏出 1 天。不过貌似古埃及人并不 care 这个，跑偏就跑偏了。
甚至到后来，亚历山大大帝治下的希腊在埃及亚历山大港建立了托勒密王朝，历法也改叫做亚历山大历后，君主托勒密三世试图修正这一偏差都没能成功，被他们的“议会”否决了。所以跑偏在埃及人看来都不叫事儿。或许正是因为他们没有这种精益求精的精神，所以才没有演化出我们今天最科学的历法吧。
我们看看别人是怎么做的，怎么就演化出今天的历法了。我们的重点是儒略历和格里高利历，看看这俩历法如何演化而来。
我们可以说，接下来历法的进化就是一部修正史，尽可能地去和至高无上的太阳神保持同步修正史。
一切要从古罗马说起
4 罗马历
公元前 8 世纪，罗马城的建立，开启了罗马王政时期。这时的罗马人也是看月亮过日子的，天文学祭司来观察天空。当他第一次看到新月时，宣布下一个月已经开始。正如前文说的，罗马人把这一天称为 Kalends。
古罗马的文化基本都是照抄古希腊的，历法也是大体沿用古希腊的雅典城邦的阴阳历法，历法主体是阴历，在此基础上通过加闰月的方法来使阴历和阳历相协调。
但罗马人没有遵循希腊人的通常做法，即月份交替 29 天和 30 天。公元前 5 世纪，罗马人将月份与月球周期分开，月不再以月相为参考。
他们采取 31 天和 29 天的混合，其中 4 个月为 31 天，7 个月为 29 天，还有可怜的 2 月是 28 天，因为 2 月是执行死刑的月份，所以人们都希望它快点过去，所以2月就要短一些。
这样一年又 355 天，然后靠往年末怼一个闰月来补齐剩下的天数，具体的做法是每两年在二月中间插入一个 27 天或 28 天的润 2 月。
注意，这里说的2月就是年末，罗马延续了新年的第一个月为 3 月的传统，因为 3 月是春暖花开，万物复苏的季节。
（注：本文中所说的 X 月完全是按照如今的叫法，并不代表当时这个月是第几个月。比如这里说的二月，指的是翻译成英语后叫做 February 的月份，并不代表它是每年的第二个月。）
好战的罗马人用战神 Mars 的名字命名了 3 月 March，这也解释了为什么 9～12 月英文分别叫做 September（第 7 月） October（第 8 月） November（第 9 月） December（第 10 月），sept, oct, nov, dec 分别是 7、8、9、10 的词根。
那我们不禁要问，为什么我们现在从 January 开始新的一年呢？这其中的历程蜿蜒曲折，但是第一推动力源自于偶然的历史事件。
到公元前 154 年，西班牙叛乱爆发，罗马人和西班牙人的民族战争打响。当时正值冬天 January 月，罗马赶上了领导人准备换届的季节。
按照法律新的执政官要在新年 March 才能上任，但是战争不等人。为了平定叛军，罗马元老院决定临时将 January 定为一年的第 1 月，这样就新任执政官就可以提前上台来带领军队干西班牙人。
就这样，顺带着 February 成为了第 2 个月，之后这个顺序便一直延续下来。
但是我们要明确一点，在后来动荡不安的罗马共和国，历法从来都是为统治阶级服务的。随着罗马共和国内政治斗争的白热化，历法越来越多的成为宗教制约政权的工具。
所以后期的罗马历就变成了有 12 个固定月份和 1 个不固定的第 13 个闰月，这第 13 个月有多长完全是由大祭司决定，由于罗马共和国执政官的任期和日历年对应，因此大祭司作为宗教领袖，可以人为地减少与他不和的执政官在任年的长度，增加其政治盟友的执政年限，因此存在着极大的滥用权力空间。
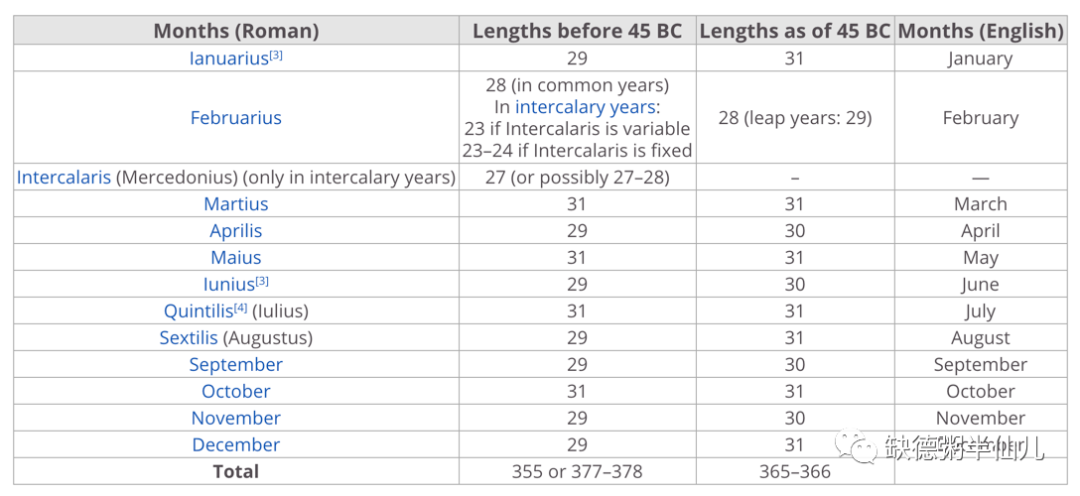
这越来越乱的历法最终在恺撒时期画上了句点，公元前 46 年，凯撒以大祭司的身份，下令改革历法，并颁布了以自己名字 Julius 命名的新立法——儒略历(Jurian Calendar)，意为尤利西斯的历法，从而结束了此前长时间的历法混乱。
5 儒略历
儒略历的诞生，简单来说就俩原因：
1、老历法乱套了
2、出现了一个权力足够大的人来新修历法
上文说到，在以前的罗马历中，每隔一年就加一个润月，这就造成了第一年 355 天，第二年 377 或 378 天。这样四年平均下来的每年的天数为 366.25 天，每年要比正常回归年多 1 天。这是个很大的误差，30 年下来就多出一个月，罗马历法势必会混乱。
上文还说到，罗马共和国建立后，将闰年的控制权授予教皇，教皇最终滥用权力，延长其政治盟友在位的年份，缩短对其手任期的年份。罗马共和国混乱时期，罗马历被当作统治权力维护工具，导致每年长短不一，极其混乱。
再后来，闰月的设定公布的越来越晚，以至于好多住在偏远地区的老百姓根本不知道日期，这还了得，老百姓不知道哪天是双 11，还怎么剁手？
后来连负责传达历法的官员们也都不干了，为啥呢？因为罗马人内讧了，军队拥兵自重，和元老院干起来了。
恺撒就是其中一位拥兵自重的军官，最终恺撒击败庞培。脱颖而出，征服了意大利，制服了养老院，强迫元老院授予他终身独裁官。自此，恺撒成为罗马共和国唯一的扛把子。
这也给了恺撒修改历法的权限，恺撒能改历法，跟他手握大权是分不开的。凯撒的改革旨在永久性地解决立法混乱问题，他想要创造了一个与太阳保持一致的历法。
口号喊得响没用，这件事情难就难在如何处理月份上。于是恺撒在和埃及艳后泛舟尼罗河后，召集了当时一大批数学家和天文学家来计算如何处理月份，这些人想出的办法我们之前也提到过，抛弃月亮拥抱太阳，将抛弃阴历拥抱阳历。
早在公元前 2 世纪，上古天文学大佬喜帕恰斯就已经可以很精确地测算出一回归年的长度大概不到 365.25 天。要凑这个数的办法就是让有些年份 365 天，有些 366 天，这样长期一平均就差不多了。365 天的年叫做平年，366 的叫做闰年。
如何分配这 365 或 366 天呢？既然已经抛弃阴历了，也就不需要看月亮了，也就意味着可以随意规定一个月的天数。因此最简单的分配方式就是将这个数除以 12，尽可能平均地分配给 12 个月，这样每个月就是 30 或 31 天。但是 2 月由于不吉利仍然维持旧罗马历的 28 天。在闰年的时候加的那一天给 2 月。
恺撒听完觉得不错，可以和天文现象对得上。这一年是公元前 46 年，恺撒决定让之前所有的混乱都在这一年有个了断吧，下一年开始使用统一的新历法，颇有秦始皇车同轨书同文的赶脚。
恺撒计划儒略历在次年（公元前 45 年）正式生效，因此他等 1 月 1 日到来再开始新的一年，这样才能和季节同步。
这样做的代价就是前一年（公元前 46 年）多出了 60 多天，创下了史上最长年份记录，BC46 共有 455 天！老百姓也洋溢着笑容拍手称快，因为他们觉得恺撒大帝让他们每个人都多活了 60 多天，LOL……
恺撒将这一年称为最后的混乱年，之后在罗马世界便会有真正统一的历法，这就是最初的儒略历，也是儒略历的 beta 版本。
为什么说是 beta 版本，还不是最终版吗？不是，因为计算出错了……出在了平闰年分配上。
应该给 365 和 366 分别赋予怎样的权重，就可以使得期望值为 365.24 或 365.25？这个问题中学生都会算，解一元一次方程嘛，每四年闰一次。可偏偏当时的人计算错了，搞成了每三年一个闰年。当然还有一些历史性原因，总之就是算错了。
这个错误在公元 8 年由恺撒的下一任屋大维改正，最终形成了大名鼎鼎的儒略历的最终版本：
1、继续沿用 1 月 1 日为新年伊始。
2、在原来的一普通年 355 天的基础上加上 10 天，其中 1、8、12 月份各加 2 天；4、6、9、11 月各加 1 天，每四年设一个闰年，润年的话 2 月再加 1 天。
因此儒略历下平均每年就是 365.25 天，很接近于一个回归年（365.24xxxx），也就是太阳绕一圈的时间，即恺撒想要尽量对上的那个基于天文的标准时间。
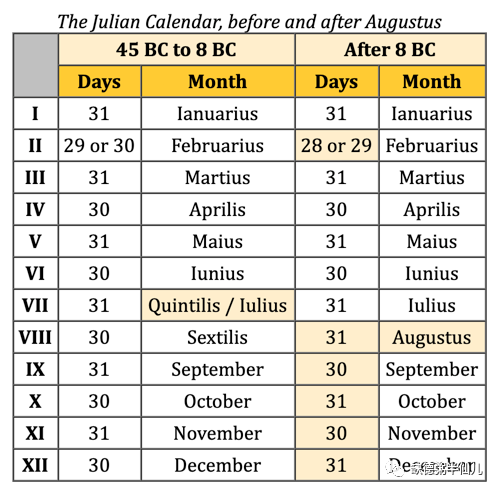
罗马元老院为了赞颂恺撒和屋大维爷叔侄，于是分别用恺撒的名字尤里乌斯和屋大维的称号“奥古斯都”命名了 7 月（July）和 8 月（August）。并且为了俩人平起平坐，让 8 月从 2 月那里借来一天变成大月（31天），然后 9 月 11 月的大月身份也平移到了 10 月和 12 月。
至此，儒略历的一年就和我们现在的一年几乎一样了，仅仅是闰月和现在不一样。
1、为什么 7 月命名为恺撒，据说是因为恺撒出生在 7 月
2、为什么从 2 月借一天，是因为在 2 月处理死囚
儒略历的颁布还有一个作用，就是基本上在整个罗马版图覆盖的地方都统一了 7 天的一周。随后又将一周的日子与太阳、月亮和肉眼可见的五颗行星联系在一起。
这为之后的基督教和一周七天紧密联系铺平了道路。君士坦丁大帝承认基督教后，正式采取一周 7 天制。
基督教合法了，随之带来了一个问题，基督教徒们继承了犹太教的传统，上帝在安息日休息，所以教徒们在安息日也要休息。而安息日是每周的周六。
但是当时的罗马公民们的习惯是每周日休息，因此教廷就将安息日从周六挪到了周日，并改名为“主日”。从此，星期日对于基督教有了特殊的意义。
300 多年后，随着基督教的合法化和国教化，儒略历作为基督教礼仪历法，传播到罗马帝国以外的地区。当一个民族或一个国家皈依基督教时，他们一般也采用负责皈依的教会的基督教历法。
就这样，儒略历在基督世界中流传了上千年，直到一个人的出现……
6 格里高利历
格里高利历是在 1582 年，时任教皇格里高利 13 世颁布的历法，也就是我们今天使用的公历，是全世界统一使用的官方历法。
我们知道，随着基督教在罗马帝国被奉为国教之后，教皇就是基督世界的精神领袖，教皇自然也负责颁布历法来指导教众。历任教皇通常选择沿用儒略历，因为儒略历还挺好用的。
直到格里高利十三世，对儒略历做了个轻微的修改，改成了我们今天所用的这样。
为啥儒略了使用了 1500 多年后，教皇给改了呢？原因有二：（1）旧的儒略历跑偏了；（2）宗教因素。
第一个原因不难想到，因为儒略历跑偏了。儒略历平均每年是 365.25 天，但一回归年是 365.24xxx，两者存在着微小的差异，这个差异在大时间尺度下也会被放大成为无法忽略的偏差，日历年每 400 年就要和回归年差出 3 天。
儒略历到格里高利时期已经用了 1500 多年，比回归年多出了 10 天左右。所以在 1582 年，教皇格里高利就颁发了命令，直接凭空消失 10 天（10.5-10.14）。
我们大致可以估算一下，时至今日，如果继续使用儒略历的话，会和格里高利历相差约 13 天。
旧历法的跑偏问题并不是到格里高利十三世时才被认识到，之前的教皇有些也意识到了这个问题，但由于种种原因，未能实施修订历法。15 世纪末，天文知识的增加和观测的精确性使得这个问题变得更加紧迫。在随后的几十年里，许多出版物呼吁改革历法，终于在格里高利十三世时实现了历法改革。
光把过去的误差填补上还不行，还得保证以后不跑偏。所以负责给教皇老哥编写历法的天文学家，提出了改变闰年的设法，凡是年数能被 4 整除的是闰年，但是年数后边是带两个“0”的“世纪年”时，必须能被 400 整除的年才是闰年，所以 1900 年不是闰年。
现在历法周期变成了 400 年，这 400 年共有 146097 天。这样平均下来一年有 365.2425 天，这一数值仅比回归年多了 26 秒，这样过 3000 年左右才会有 1 天的误差。
对于这个精度教皇大哥很满意，于是发布诏书颁布新立法。这个新历法就被叫做格里高利历，也就是我们现在用的公历。
所以简单来说，格里高利历就是恢复奥古斯都时期儒略历的版本（1 月 1 日为元旦），并且做了一点点小的闰月修正，仅此而已。
当然，教皇大哥也不是心血来潮拍脑袋的决定，而是由于某些宗教上的动机。儒略历的跑偏没错，但教皇大哥真正关心的是这种跑偏造成了春分点提前到来了，而春分本应该在 3 月 21 日出现。为什么教皇大哥这么纠结春分点呢？这就涉及到下面要说的宗教因素了。
7 宗教因素
虽然罗马天主教会曾经对科学和天文学进行了长期而激烈的斗争，但总的来说，中世纪后半期教会也给予了天文学研究大量的资金和社会支持，包括在各地大教堂的塔楼改造作为太阳观测站。
教会这么做不一定是为了知识而寻求知识，相反，它希望通过投资得到一些实际的回报，最重要的回报就是改进日历。
回到刚才的问题，教皇为什么纠结春分，因为春分对基督教会很重要。
1、春分是万物复苏的时间
2、春分是儒略历的新年伊始
3、春分传说是耶稣受孕日（所以推定 9 个月后的 12 月 25 日是圣诞节）
4、它是计算复活节日期的基础
第四点最重要。教皇为了使当前的复活节日期与早期教会引入复活节时的日期相一致。
当然基督教教皇和官员们也并非完全就是要虔诚地庆祝他们的上帝复活，更多的也是出于统治的需要，以及加强教会的权力和团结。
于是教皇和教会官员将希望寄托在天文学家上，希望天文学家可以依照科学来确定日期，改进日历。
想要完全理解上述前因后果，我们要补充必要的基督教背景知识。时间回到一千多年前。
我们知道，在恺撒屋大维颁布儒略历的时代，基督教还是异教。直到 313 年君士坦丁皇帝颁布《米兰赦令》，第一次承认基督教的合法性，才结束了基督教在罗马近 300 年的苦难历程。到了公元 525 年，人们第一次使用公元纪年法，将耶稣降生的那年计作公元元年。
但是没过几年，基督教内部在耶稣的神性上出现了教义之争。君士坦丁非常恼火，哥承认了你们，你们自己居然为了芝麻大点的事内讧了。于是他决定要召开一次基督教全体会议，以便统一思想。
这就是著名的“基督教一大”——尼西亚大公会议，发生在公元 325 年。这次会议对我们接下来要说的内容很重要。这次会议没有调和双方的矛盾，而是直接简单粗暴的捧一踩一。这也为后面基督教分裂埋下了最直接的伏笔。到了 380 年，另一位著名的罗马皇帝狄奥多西宣布取缔了罗马信奉了一千多年的多神教，要求罗马全体公民信仰基督教。392 年基督教正式成为罗马国教，从一个备受歧视的异教变成一个一家独大的宗教信仰和意识形态。
尼西亚大公会议对格里高利历的重要意义在于，在这次会议上，基督教高层领导们明确规定全世界所有基督徒都应在同一天庆祝复活节，并且明确确定了这一天是哪天，即颁布了“法定”的复活节日期：
春分之后的第一个满月后的第一个星期日
教皇认为应该以尼西亚大会召开的 325 年为基准，所以将 1582 年完全复刻了 325 年。正如前文所说，这么做就需要凭空抹去多出来的 10 天。（选择抹去 10.5-10.14 是因为这 10 天内没有基督教的重要日子）
其中网上传的神乎其神的“惊！历史上竟消失了10天！”其实也没啥大不了的，其实这10天根本就没有消失，只是人们因为特殊的原因改了计时的历法，就像人们为了方便随意选取参考系一样，正如物体的客观存在并不依赖于参考系的选择，历史上的10天不因历法的切换而消失。
复活节对基督徒们意义可就大了，是和圣诞节并称的基督教两大节日。根据《圣经》中记载，耶稣受难后的第三天复活，告诉他的门徒们离开犹太人的大本营——以色列，世界那么大，你们去罗马看看。基督徒们认为耶稣受难日是公元 33 年 4 月 3 日（星期五），三天后（星期日）复活。
有趣的是本文主角牛顿也曾指出受难日并不是这一天，但结果表明牛顿自己把历法搞错了，就像后人搞错他生日一样。
试想一下，复活节日期的精确规定这件事情，就很考验历法的精确程度了，历法要不准了，全世界基督徒们就可能有不同的复活节了。
我们知道，复活节是基督教最重要的节日之一，但是彼时的庆祝耶稣基督复活的盛典已经成为教会的一个官僚危机。到了 12 世纪，复活节的误差已经不能忍了。
儒略历被抛弃就是因为出了这样的问题，前文说到，儒略历跑偏了，春分点跑偏了，复活节就不准确了，准确的说是历法层面的复活节和天文学层面的复活节对不上了，因为日期已经到 3 月 21 日了，但是天文学上还没有到春分。
我们就拿今年 2021 年举例子，按照天文学，今年春分是 3 月 20 日，下一个满月是 3 月 28 日，这天正好是周日，所以复活节就得是再下一个周日 4 月 4 号。但是如果按照儒略历，今年的复活节是 5 月 2 日（换算成公历）。
8 格里高利历的普及
各个国家采用 "新 "历法的时间也参差不齐，格里高利历最初是由欧洲天主教国家及其海外属地采用的，传统天主教国家如法国、西班牙、水果牙、意大利等都在 1582 年当年就改用新历法。
新教和东正教国家不受天主教皇的管辖，因此一开始并没有赏脸，直到一个多世纪以后才陆续慢慢开始使用新历，特别是在英国（以及其美洲殖民地的国家）在 1752 年 9 月 14 日才采用新历法，这时牛顿早已去世了。
插曲：也就是说，包括美国在内的这些国家在1752年才发生“消失的10天”
这就解释了为什么牛顿有俩生日，牛顿在英国出生时英国使用的还是儒略历，所以牛顿的出生仍被记录为 1642 年的圣诞节，尽管意大利的这一年已经是 1643 年。而伽利略去世时（1642 年），其祖国意大利以及开始使用格里高利历 60 年了，自然用新历记录，所以在网上查伽利略就只有一个祭日。
还有一件与牛顿伽利略情况类似的事件
莎士比亚和塞万提斯这两位大文豪，似乎正好在同一天去世（1616 年 4 月 23 日），但其实不是。各位小伙伴不妨算一下，谁先死的，早了几天？
然而这一历法差异带来的巧合被联合国教科文组织拿来做文章，也就有了我们现在每年 4 月 23 日的 "世界图书和版权日"。
荷兰国王兼英国国王威廉三世要从荷兰出发前往英国加冕，荷兰这边说我们威廉大大 11 月 11 日出发，英国这边则说俺们陛下 11 月 5 日就到了……
By the way, 新历在明清时期由西方传教士传入我国，我国明确使用格里高利历是在辛亥革命之后，满清灭亡，没有皇帝也就没有年号纪年法了，于是中华民国政府宣布 1912 年开始使用新历。当然还有比我过更晚使用新历的国家，最墨迹的是沙特，沙特 2016 年才使用新历。
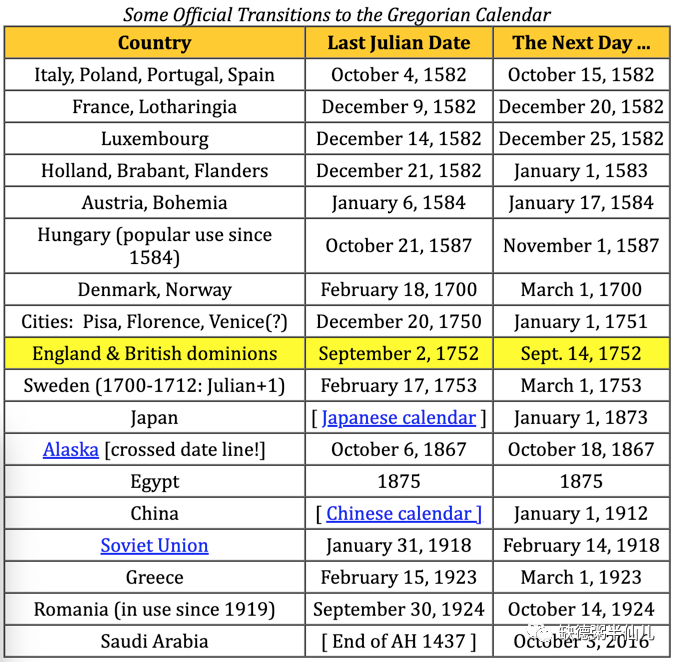
9 变来变去的新年伊始日
在回归主题之前，我们还需要最后搞清楚一个问题，那就是新年从哪一天开始？搞清楚这个问题，我们才好说究竟两件事情是否发生在同一年。
这个问题从最开始阴历流行的时候就存在了。我们知道，每月的开始时间是确定的，只要看到新月就是新的一月。但是每年从哪天开始呢？太阳在哪个位置才算新的一年？这就给统治者留下了空间，他们可以任意将某个月当作第一个月。
比如陈胜吴广起义，在秦二世元年 7 月爆发，次年 12 月结束。乍一看好像起义持续了一年多。但其实不是这么回事，因为秦始皇登基后规定以 10 月为新年第一个月，所以起义也就持续了 5 个多月。
再比如法国大革命后，建立共和国，同时建立共和历，并以建国的当月定为第一个月，同时出现了雾月、热月等称谓。对应的雾月政变和热月政变也是在法兰西第一共和国期间爆发的。
从两河文明开始，人们就偏爱春天，春暖花开万物复苏在人们看来是神的恩泽，因此大多数文明都将春天作为新年伊始，尤其是春分日，昼夜平分的特点似乎也象征着某种神谕。
因此最早期的元旦都定在三月，由于当时以阴历为主，也就是看月亮定日子。所以新月和满月就成为最特殊的两天，分别对应着 1 日和 15 日（我国的初一和十五）。最初人们将元旦定为 1 号，后来发现 15 号更接近春分，就改成 15 号。
元旦：我真的是躲得过初一躲不过十五惹……
好战的罗马人更是用战神 Mars 的名字命名了三月 March。
然后我们前文提到了，由于西班牙战争的原因，公元前 153 年罗马元老院将第一个月从 3 月改到了 1 月，儒略历更是将元旦钉死在了 1 月 1 日。
然而，在中世纪的欧洲，基督教（这里我们特指天主教）开始豪横起来。教皇认为 1 月 1 日这个日子很不基督教，既不是基督教的传统节日，也不是一个良辰吉日。
毕竟当时元旦改为 1 月 1 日时还没有基督教什么事，是世俗皇帝规定的。上帝的归上帝、恺撒的归恺撒。而中世纪教俗之争狂热，双方水火不容。
教皇为了彰显自己的厉害，宣布在 1 月 1 日庆祝新年是异教行为，并在公元 567 年废除了 1 月 1 日作为一年的开始。但是并没有规定一个新的元旦。这导致在整个中世纪基督教欧洲的不同时期和不同地方，有着不同的元旦，大都是和基督教有关的日期：12 月 25 日（圣诞）、3 月 1 日（传统春天良辰吉日）、3 月 25 日（耶稣受孕日——报喜节）和复活节庆祝新年。
到了中世纪后期（14、15 世纪），整个欧洲的新年伊始开始逐渐向报喜节统一。因为报喜节不仅是耶稣受孕日，还是古罗马时期的春分日，双厨狂喜，其中就包括我们要说的英国。
这就是为什么上文我们说，格里高利将元旦重新定为 1 月 1 日。
10 再论牛顿生日
在一般情况下，消失的 10 天作为历法记录选择的分界点，1582 年 10 月 15 日之前发生的事件的日期一般按照 1 月 1 日开始的儒略历，不需要转换为格里高利历的对应日期。而在这之后的就要用格里高利历来记录了。
但是，并不是所有国家都同时开始使用格里高利历，在历史上相当一段时间内，在欧洲有些国家已经投入了新历的大怀抱，有些国家还在使用着旧历。
因此在这段时间内，人们为了明确地指明一个日期，往往要同时使用旧历和新历，尤其是英国喜欢在旧历前面标上 O.S.代表 “旧式”(Old Style)。
我们已经知道，牛顿出生的时候，英国用的还是儒略历。所以我们看维基百科的牛顿生日的描述为：
前面的 O.S.就表示在旧历表示下牛顿的生日是 1642.12.25。
值得注意的是，我们知道新旧两历的元旦时间不一样，因此如果某人生日特别巧处在两者之间，就会有一些麻烦了，可能会连年份都不一样。
我举个例子，假如英国人 Three Zhang 出生于新历的 1700 年 3 月 1 日，那么他在写自己生日时，要加上「O.S. 1699.3.1」。旧历中新年伊始是 3 月 25 日，所以张三的生日在旧历中还处在 1699 年。
另一方面，说霍金出生（1942 年 1 月 8 日）比伽利略逝世（1642 年 1 月 8 日）整整晚了 300 年，这么说没毛病，因为这两件事都记录在格里高利历上。
11 历法的未来
著名天文学家威廉·赫歇尔的儿子约翰·赫歇尔眼光长远，他觉得人类还能生存千秋万代，因此试图将历法周期从 400 改成 4000（即 5000 这种年份也不润）来进一步减少每年的平均天数，增加精度。
但是这一建议一直未被采纳。不过未来减少每年天数似乎是势在必行的事情，因为地球自转越来越慢，每一天时间越来越长。
不过，随着科学的发展和技术的进步，今天我们人类已经有了很精确的计时工具。时间也从原来的度量方式变为理论上定死的数值。
之后我们的时间刻度和历法要怎样再修改以拟合天文现象，小伙伴们可以大开脑洞想象一下。
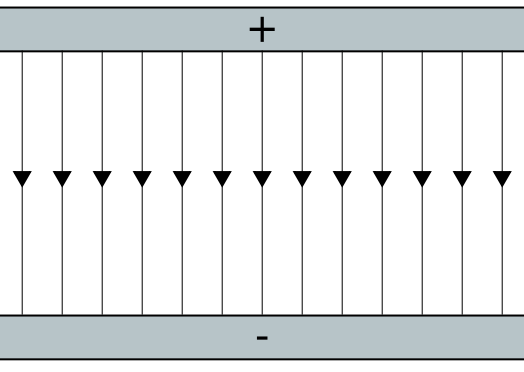
什么是高中物理？
