\section{光的干涉}
\subsection{单色光波}
\subsubsection{单色光波的描述}
单色光波的波函数是
\begin{align}
\vec E(p,t)=\vec E_0(p)\cos[\omega t-\varphi(p)]
.\end{align}
理论上单色光波必须满足：
\begin{enumerate}
\item 电磁场频率\(\omega\)不变；
\item 空间各点的光波振幅\(\vec E_0(p)\)、初始相位\(\varphi_0(p)\)不随时间变化；
\item 光波波列无限长。
\end{enumerate}
第三点是因为根据Fourier分析，对有限长的一列光波进行Fourier变换后可以发现，这列光波可以看成是由不同频率的无限长单色平面波线性叠加而成的。这一点将在本节的最后予以简单的说明。\\
\phantom{awd}\par
单色平面波的波函数
\begin{align}
\vec E(p,t)=\vec E_0\cos(\omega t-\vec K\cdot\vec r+\varphi_0)
.\end{align}
\phantom{awd}\par
单色球面波的标量波函数
\begin{align}
E(p,t)=\frac{A_0}{r}\cos(\omega t-kr+\varphi_0)
.\end{align}
其振幅正比于\(1/r\)，这来自于能量守恒定律，等下讲了光强便会证明。\\
\phantom{awd}\par
现在将波函数改写为复指数函数的形式，则单色光波的波函数为
\begin{align}
\tilde E(p,t)=E_0(p)\mathrm e^{-\mathrm i[\omega t-\varphi(p)]}
=E_0(p)\mathrm e^{\mathrm i\varphi(p)}\mathrm e^{-\mathrm i\omega t}
=\tilde E_0(p)\mathrm e^{-\mathrm i\omega t}
.\end{align}
对于单色光场的波函数，时间振荡因子\(\mathrm e^{-\mathrm i\omega t}\)都是相同的，所以常常略去不写，剩下的空间分布因子是光场的复振幅\(\tilde E_0(p)\)。\\
光强是光的平均能流密度，可以方便地写成复振幅的形式：
\begin{align}
I=\left<\vec E,\vec E \right>
=\tilde E_0^*(p)\tilde E_0(p)
.\end{align}
回到球面波的振幅问题，根据能量守恒，在没有光能吸收的情况下，在单位时间内以点光源为球心的球面上的总光能量是相同的，而光强是单位时间单位面积上的能量，所以单位时间内半径为\(r\)的球面上的总能量是\(W=4\pi r^2I\)，又\(I=A_0^2/r^2\)，因此\(W=4\pi A_0^2\)为常数，满足能量守恒。

\newpage
\subsubsection{单色光波的叠加}
设有\(n\)个频率、振动方向相同的单色光波发生线性叠加，其中第\(i\)列光波为
\begin{align*}
\tilde E_i(p,t)=\tilde E_{0i}(p)\mathrm e^{-\mathrm i\omega t},
\end{align*}
则点\(p\)处的总光振动为
\begin{align*}
\tilde E(p,t)=\sum_{i=1}^n\tilde E_i(p,t)=\left\{\sum_{i=1}^n\tilde E_{0i}(p) \right\} \mathrm e^{-\mathrm i\omega t}.
\end{align*}
总振幅为
\begin{align*}
\tilde E_0(p)=\sum_{i=1}^n\tilde E_{0i}(p).
\end{align*}
\phantom{awd}\par
以两列光波的叠加为例，设
\begin{align*}
\tilde E_0(p)=\tilde E_{01}(p)+\tilde E_{02}(p)=E_{01}\mathrm e^{\mathrm i\varphi_1}+E_{02}\mathrm e^{\mathrm i\varphi_2},
\end{align*}
计算合振动的振幅：
\begin{align}
\tilde E_0^2(p)&=\tilde E_0^*(p)\tilde E_0(p)\notag \\
&=(E_{01}\mathrm e^{-\mathrm i\varphi_1}+E_{02}\mathrm e^{-\mathrm i\varphi_{2}})(E_{01}\mathrm e^{\mathrm i\varphi_1}+E_{02}\mathrm e^{\mathrm i\varphi_{2}})\notag\\
&=E_{01}^2+E_{02}^2+E_{01}E_{02}[\mathrm e^{\mathrm i(\varphi_1-\varphi_2)}+\mathrm e^{-\mathrm i(\varphi_1-\varphi_2)}]\notag\\
&=E_{01}^2+E_{02}^2+2E_{01}E_{02}\cos(\varphi_1-\varphi_2)
.\end{align}
再计算合振动的初相位：
\begin{align}
\tilde E_0(p)&=E_{01}\cos \varphi_1+E_{02}\cos \varphi_2+\mathrm i(E_{01}\sin \varphi_1+E_{02}\sin \varphi_2),\notag\\
\tan \varphi&=\frac{E_{01}\sin \varphi_1+E_{02}\sin\varphi_2}{E_{01}\cos\varphi_1+E_{02}\cos\varphi_2}
.\end{align}
\phantom{awd}\par
现在考虑两个振动方向相同、振幅相等而频率相差很小的单色光波的叠加，结果会产生“光拍”现象。\\
设角频率为\(\omega_1,\omega_2\)的两个单色光波沿着\(z\)方向传播，其波函数为
\begin{align*}
E_i=E_0\cos(\omega_it-k_iz),\quad i=1,2,
\end{align*}
两个光波叠加
\begin{align}
E&=E_0\cos(\omega_1t-k_1z)+E_0\cos(\omega_2t-k_2z)\notag \\
&=2E_0\cos \left\{ \frac{1}{2}[(k_1+k_2)z-(\omega_1+\omega_2)t] \right\}\cdot\cos \left\{ \frac{1}{2}[(k_1-k_2)z-(\omega_1-\omega_2)t] \right\}
.\end{align}
设平均角频率\(\overline \omega\)、调制角频率\(\omega_m\)为
\[
\begin{cases}
\overline \omega=\frac{1}{2}(\omega_1+\omega_2),\\ \overline k=\frac{1}{2}(k_1+k_2),
\end{cases}\quad
\begin{cases}
\omega_m=\frac{1}{2}(\omega_1-\omega_2),\\
k_m=\frac{1}{2}(k_1-k_2),
\end{cases}
\]
并设
\begin{align*}
A=2E_0\cos(k_mz-\omega_mt),
\end{align*}
则合成波可以写为
\begin{align}
E=A\cos(\overline kz-\overline \omega t)
.\end{align}
这意味着合成波可以看作一个频率为\(\overline \omega\)而振幅随着时间和位置在\(-2E_0\)和\(2E_0\)之间变化的高频波列。由于光波频率很高，\(\omega_1\thickapprox \omega_2\)，因而\(\overline \omega \gg\omega_m\)，从而振幅\(A\)变化缓慢而光振动\(E\)变化极快。\\
合成波的光强为
\begin{align*}
I=4E_0^2\cos^2(k_mz-\omega_mt)
,\end{align*}
可以看出其随着时间和位置在\(0\)和\(4E_0^2\)之间变化。这种强度时大时小的现象称为“拍”，由上可知拍频等于\(2\omega_m=\omega_1-\omega_2\)。\\
\phantom{awd}\par
单色光波是理想的光波，实际上波都是由许多不同频率的单色波按照一定方式叠加而成，叠加结果成为波包或波群。\\
光波的等相面传播速度是波群的相速度
\begin{align}
v_p=\frac{\omega}{k}
,\end{align}
等幅面传播速度是波群的群速度
\begin{align}
v_g=\frac{\mathrm{d}\omega}{\mathrm{d}k}
.\end{align}
由此可以得到群速度\(v_g\)和相速度\(v_p\)的关系
\begin{align}
v_g&=\frac{\mathrm{d}\omega}{\mathrm{d}k}
=\frac{\mathrm{d}(kv_p)}{\mathrm{d}k}
=v_p+k \frac{\mathrm{d}v_p}{\mathrm{d}k}, \notag \\
&=v_p+\frac{2\pi}{\lambda}\frac{\mathrm{d}v_p}{-\frac{2\pi}{\lambda^2}\mathrm{d}\lambda}
=v_p-\lambda\frac{\mathrm{d}v_p}{\mathrm{d}\lambda}
.\end{align}
这意味着群速度和相速度的差值取决于\(\frac{\mathrm{d}v_p}{\mathrm{d}\lambda}\)，其正负即色散关系。\\
波携带的能量与振幅的平方成正比，因此群速度代表能量传播的速度，即信号速度。\\
\phantom{awd}\par
严格地推导波包的群速度，需要将波包展成Fourier积分
\begin{align}
\tilde E(x,t)=\frac{1}{2\pi}\int_{k_0-\Delta k/2}^{k_0+\Delta k/2}E_0(k)\mathrm e^{-\mathrm i(\omega t-kx)}\,\mathrm dk
.\end{align}
可以看出波包是由中心频率为\(k_0\)，频谱范围为\(\Delta k\)的单色光以不同的权重\(E_0(k)\)叠加而成的，这里\(E_0(k)\)取决于谱线的线型。\\
对于准单色波包，频率范围\(\Delta k\)很小，近似取
\begin{align*}
E_0(k)=E_0(k_0),
\end{align*}
这是一个常数，直接提到积分号外。\\
对于\(\omega(k)\)，令\(k'=k-k_0\)，将\(\omega(k)\)展开到一阶
\begin{align*}
\omega(k)=\omega(k_0)+\frac{\mathrm{d}\omega}{\mathrm{d}k}\bigg |_{k=k_0}k'.
\end{align*}
从而被积函数的指数
\begin{align*}
\mathrm e^{-\mathrm i(\omega t-kx)}=\mathrm e^{-\mathrm i(\omega_0t-k_0x)}\mathrm e^{-\mathrm i\left( \frac{\mathrm{d}\omega}{\mathrm{d}k}t-x \right)k' }.
\end{align*}
于是
\begin{align}
\tilde E(x,t)&=\frac{1}{2\pi}E_0(k_0)\mathrm e^{-\mathrm i(\omega_0t-k_0x)}\int_{-\Delta k/2}^{+\Delta k/2}\mathrm e^{-\mathrm i\left( \frac{\mathrm d\omega}{\mathrm dk}t-x \right)k' }\,\mathrm dk'\notag \\
&=\frac 1{2\pi}E_0(k_0)\mathrm e^{-\mathrm i(\omega_0t-k_0x)}
\frac{
\mathrm e^{\mathrm i
\left(\frac{\mathrm d\omega}{\mathrm dk}t- x\right)\frac{\Delta k}{2}
}
-\mathrm e^{-\mathrm i
\left(\frac{\mathrm d\omega}{\mathrm dk}t-x
\right)\frac{\Delta k}{2}
}
}{\mathrm i\left(\frac{\mathrm d\omega}{\mathrm dk}t-x
\right)}\notag\\
&=\frac 1{2\pi}E_0(k_0)\mathrm e^{-\mathrm i(\omega_0t-k_0x)}
\frac{2\sin\left[\left(\frac{\mathrm d\omega}{\mathrm dk}t-x\right)\frac{\Delta k}{2}\right]}{\frac{\mathrm d\omega}{\mathrm dk}t-x}\notag\\
&=\frac{E_0(k_0)}{\pi}\frac{\sin\left[\left(\frac{\mathrm d\omega}{\mathrm dk}t-x\right)\frac{\Delta k}{2}\right]}{\frac{\mathrm d\omega}{\mathrm dk}t-x}\mathrm e^{-\mathrm i(\omega_0t-k_0x)}
.\end{align}
其中\(\frac{E_0(k_0)}{\pi}\frac{\sin \left[ \left(\frac{\mathrm d\omega}{\mathrm dk}t-x\right) \frac{\Delta k}{2}\right] }{\frac{\mathrm{d}\omega}{\mathrm{d}k}t-x }\)是振幅包络因子，\(\mathrm e^{-\mathrm i(\omega_0t-k_0x)}\)是高频相位因子。\\
波包的群速度可以从振幅包络因子的最大处条件求出，由\(\lim_{x\rightarrow 0}\frac{\sin x}{x}=1\)，令\(\frac{\mathrm d\omega}{\mathrm dk}t-x=0\)，求出\(v_g=\frac{\mathrm d\omega}{\mathrm dk}\)。\\
\phantom{awd}\par
下面再来讨论波列长度与频率范围的关系。由振幅包络因子可以看出，\(t\)时刻波包振幅最大处为\(x_m=v_gt\)，此时振幅由最大值向两边衰减，令\(\sin(\cdots)=0\)可知当\(x=v_gt\pm \frac{2\pi}{\Delta k}\)时振幅为零，可以认为这里就是波包的两个端点。因此波包也可视作有限长度的波列，波列长度的数量级为
\begin{align}
l_c&\thickapprox \frac{2\pi}{\Delta k},\notag \\
&=\frac{2\pi}{\frac{2\pi}{\lambda^2}\Delta \lambda}=\frac{\lambda^2}{\Delta \lambda}
.\end{align}
这意味着波列长度\(l_c\)和波包所包含的单色分波的波长范围成反比，波列越长，波列所包含的单色分波的波长范围就越窄，当波列长度为无限长时\(\Delta \lambda=0\)，这就是单色光波。\\
谱线宽度可以度量光波的单色性，谱线越窄，单色性越好，同样，光波的波列长度也可以度量光波的单色性，波列越长，单色性越好。综上，两种说法——“光是由有限长的波列组成的”和“光是非单色的”是等效的，它们是光源同一性质的不同表述，前者着重光波的空间长度，后者则从光波的频谱着眼。\\
设光源的发光时间为\(\tau_0\)，则波列长为\(l_c=c \tau_0 \)，又\(\Delta \nu=c \Delta \lambda/\lambda ^2\)，代入得到
\begin{align}
\tau_0\Delta \nu \thickapprox 1
.\end{align}
因此光源的发光时间\(\tau_0 \)也是单色性的度量。

\newpage
\subsection{光干涉的相干条件}
两束或以上的光波在一定条件下叠加，在重叠区域形成稳定的、不均匀的光强分布，出现明暗相间或彩色的条纹，这种现象称为\textbf{光的干涉}。\\
考虑两个振动方向、频率、初相位相同的单色点光源发出的两列球面波
\begin{align*}
\tilde E_i(p,t)=E_{0i}\mathrm e^{\mathrm i(kr_i-\varphi_0)}\mathrm e^{-\mathrm i\omega t},
\end{align*}
叠加后的光强分布
\begin{align}
I(p)&=E_{01}^2+E_{02}^2+2E_{01}E_{02}\cos[k(r_1-r_2)],\notag \\
&=I_1+I_2+2\sqrt{I_1I_2}\cos[\delta (p)]
.\end{align}
其中\(\delta (p)\)是两光波在点\(p\)处的相位差，这就是\textbf{光强分布基本公式}。\\
产生干涉的必要条件有三条：
\begin{enumerate}
\item 频率相同；
\item 存在相互平行的振动分量；
\item 相位差稳定。
\end{enumerate}
为了使相遇的两列光波具有稳定的相位差，必须设法将同一光源/同一原子发出的同一波列分成两束，然后再重叠起来，这样在重叠区就能产生稳定的干涉场/光强空间分布。所以上面计算的叠加的两列光波具有相同的振动方向、频率、初相位。\\
\phantom{awd}\par
根据光强分布基本公式可知，满足
\begin{align*}
\delta (p)=
\begin{cases}
2m\pi,\\
(2m+1)\pi，
\end{cases}
\end{align*}
的点光强有极大/极小值。\\
但是若两列光波经过不同的介质，这时它们的相位差就是
\begin{align*}
\delta (p)=\frac{2\pi r_1}{\lambda_1}-\frac{2\pi r_2}{\lambda_2 },
\end{align*}
计算就很不方便，这时可以转化为
\begin{align*}
\delta (p)=\frac{2\pi}{\lambda }(n_1r_1-n_2r_2)=\frac{2\pi}{\lambda }\Delta l(p),
\end{align*}
这里\(\Delta l(p)\)是两列相干光在叠加点处的光程差。\\
可以得到\textbf{光程差判据}
\begin{align}
\Delta l(p)=
\begin{cases}
m \lambda,\\
(m+1/2)\lambda.
\end{cases}
\end{align}
干涉现象的可见性由干涉条纹的反衬度描述：
\begin{align}
\gamma =\frac{I_M-I_m}{I_M+I_m}.
\end{align}

\newpage
\subsection{Young's双缝干涉}
\subsubsection{干涉条纹的基本特征与光强分布}
光程差
\begin{align}
\Delta l&=r_2-r_1\doteq d\sin\theta'\doteq d\sin\theta\notag\\
&\doteq d\tan\theta=xd/D .
\end{align}
干涉极值位置
\begin{align}
x=
\begin{cases}
mD \lambda /d,\\
(m+1/2)D \lambda /d.
\end{cases}
\end{align}
干涉条纹间距
\begin{align}
\Delta x=D \lambda /d.
\end{align}
光强空间分布
\begin{align}
I&=2I_0+2I_0\cos(2\pi \Delta l/ \lambda )\notag \\
&=4I_0\cos^2\left(\pi\Delta l /\lambda \right)\notag\\
&=4I_0\cos^2\left( \frac{\pi d}{D \lambda }x \right)
.\end{align}
\subsubsection{最高可分辨条纹的级数}
波长\(\lambda \)的\(m'+1\)级极大位置在
\begin{align*}
x=(m'+1) \frac{D}{d}\lambda ,
\end{align*}
而波长\(\lambda +\Delta \lambda \)的\(m'\)级极大位置在
\begin{align*}
x=m'\frac{D}{d}(\lambda +\Delta \lambda ),
\end{align*}
因此干涉条纹的最大级数是
\begin{align}
m'=\frac{\lambda }{\Delta \lambda }.
\end{align}
与之相对应的光程差称为\textbf{最大相干光程差}
\begin{align}
\Delta l_M=\frac{\lambda^2}{\Delta \lambda },
\end{align}

\newpage
\subsubsection{干涉条纹的移动和光源的移动的关系}
光程差
\begin{align*}
\Delta l=R_2-R_1+r_2-r_1,
\end{align*}
下面是近似的艺术
\begin{align*}
&R_2-R_1\doteq \alpha d\doteq QS_2\\
&\alpha \doteq \frac{d/2}{l_2}=\frac{\updelta s}{l_1}\\
&l=l_1+l_2\doteq\left( \updelta s+\frac{d}{2} \right)\frac{1}{\alpha }\\
&\alpha \doteq \frac{\updelta s+d/2}{l} \\
&R_2-R_1\doteq \alpha d\doteq \left( \frac{\updelta s+d/2}{l} \right)d\doteq \frac{d}{l}\updelta s.
\end{align*}
综上代入有
\begin{align}
\Delta l=\frac{d}{l}\updelta s+\frac{d}{D}\updelta x=\frac{d}{D}\left( \updelta x+\frac{D}{l}\updelta s \right) .
\end{align}
计算零级条纹的位置
\begin{align}
\updelta x=-\frac{D}{l}\updelta s.
\end{align}
\subsubsection{光源的临界宽度和空间相干性}
若两组干涉条纹彼此相差半个条纹间距，则二者干涉花样互补，叠加后屏幕上光强处处相等，不能观察到干涉条纹，故有
\begin{align*}
&\updelta x=\frac{1}{2}\Delta x=\frac{D}{2d}\lambda, \\
&\updelta s=\frac{l}{D}\updelta x=\frac{l \lambda }{2d}.
\end{align*}
于是线光源的临界宽度为
\begin{align}
b_c=2\updelta s=\frac{l \lambda }{d}.
\end{align}
\phantom{awd}\par
现在从具体的干涉装置中解脱出来，反过来提问题：给定宽度为\(b\)的扩展光源，在它照明的空间中多大范围内的两个次级光源\(S_1,S_2\)还是相干的？不妨把上式倒过来
\begin{align*}
d<\frac{l \lambda }{b}=d_c,
\end{align*}
这里\(d_c\)正比于距离\(l\)，因此用\textbf{干涉孔径角}\(\beta =d/l\)来度量相干范围更加方便。现在最大干涉孔径角\(\beta _c=d_c/l\)是相距\(d_c\)的两个点光源\(S_1,S_2\)对光源中心所张的角度，在最大干涉孔径角以外的两个点光源看作不相干的，在最大干涉孔径角以内的两个点光源则有一定程度的相干性，即
\begin{align}
b \beta _c\thickapprox \lambda .
\end{align}
这意味着最大干涉孔径角\(\beta _c\)与光源宽度\(b\)成反比，这就是\textbf{空间相干性的反比公式}。
\subsubsection{干涉条纹的反衬度}
考虑沿\(s\)方向扩展、宽度为\(b\)的线光源，每一元光源宽度为\(\mathrm ds\)，看作独立点光源，则扩展光源上点\(s\)处的元光源在屏幕上点\(x\)处产生的光强为
\begin{align*}
\mathrm dI=2I_0 \left[ 1+\cos \left(\frac{2\pi}{\lambda }\Delta l\right) \right] \,\mathrm ds,
\end{align*}
其中\(\Delta l\)是\(s,x\)的函数，代入得到
\begin{align}
\mathrm dI=2I_0\left\{ 1+\cos \left[\frac{2\pi}{\lambda }\left(\frac{d}{l}s+\frac{d}{D}x\right)\right] \right\}\,\mathrm ds.
\end{align}
于是宽度为\(b\)的扩展光源在点\(x\)处的合成光强
\begin{align}
I&=\int_{-b/2}^{+b/2} 2I_0\left\{ 1+\cos \left[\frac{2\pi}{\lambda }\left(\frac{d}{l}s+\frac{d}{D}x\right)\right] \right\}\,\mathrm ds\notag \\
&=2I_0b+2I_0\int_{-b/2}^{+b/2}\cos \left[\frac{2\pi}{\lambda }\left(\frac{d}{l}s+\frac{d}{D}x\right)\right]\,\mathrm ds\notag\\
&=2I_0b+2I_0\frac{\lambda l}{2\pi d}\left[\sin\left(\frac{2\pi d}{\lambda l}\frac{b}{2}+\frac{2\pi d}{\lambda D}x\right)-\sin\left(-\frac{2\pi d}{\lambda l }\frac{b}{2}+\frac{2\pi d}{\lambda D}x\right)\right]\notag\\
&=2I_0b+2I_0 \frac{\lambda l}{\pi d}\sin\left(\frac{\pi db}{\lambda l}\right) \cos\left(\frac{2\pi d}{\lambda D}x\right)\notag\\
&=2I_0b+2I_0 \frac{\lambda}{\pi \beta }\sin \left( \frac{\pi b \beta }{\lambda } \right) \cos \left( \frac{2\pi d}{\lambda D}x \right) \notag\\
&=2I_0b \left[ 1+\frac{\sin u}{u}\cos \left( \frac{2\pi d}{\lambda D}x \right) \right]
.\end{align}
其中\(\beta =\frac{d}{l},u=\frac{\pi b \beta }{\lambda }\)。\\
因此反衬度为
\begin{align}
&I_M=2I_0b \left( 1+\left| \frac{\sin u}{u} \right| \right),\notag \\
&I_m=2I_0b \left( 1-\left| \frac{\sin u}{u} \right| \right),\notag\\
&\gamma =\left| \frac{\sin u}{u} \right| .
\end{align}
可见随着光源宽度\(b\)的增大，反衬度经过一系列极大值和零值振荡地趋近于零。第一个零点\(u=\pi \)，正是临界宽度\(b=\lambda /\beta \)。
\newpage
\subsubsection{例题：Fresnel双面镜干涉}
设光源到双面镜的镜面相交点的距离为\(r\)，双面镜的中心到屏幕的距离为\(l\)，\(S_1,S_2\)分别是光源\(S\)为双面镜所成的虚像，屏幕与\(S_1,S_2\)的中垂线垂直，光波的波长为\(\lambda \)，测得屏幕上干涉条纹的间距为\(\Delta x \)，求：
\begin{enumerate}
\item 两镜夹角\(\theta \)、屏幕上亮条纹总数\(N\)；
\item 若单色光源宽度为\(b\)，求光源的临界宽度\(b_c\)。
\end{enumerate}
\textbf{解}\quad 1.由几何关系易知
\begin{align}
S_1S_2=2r\tan \theta .
\end{align}
设屏幕上一点\(P\)到直线\(OO'\)的距离为\(x\)（当点\(P\)在\(OO'\)上方时\(x>0\)，反之则\(x<0\)），设角\(PO'O\)为\(\phi \)，则可近似
\begin{align}
&\tan \phi =\frac{2}{r+l} \doteq \sin \phi\notag .
\end{align}
由于\((r+l)\ll S_1S_2\)，\(S_1S_2\)与过点\(S_1\)到\(PS_2\)的垂线的夹角近似为\(\phi \)，光程差\(\Delta l\)近似为\(S_1S_2\sin \phi \)，从而
\begin{align}
\Delta l&=S_1S_2\sin \phi \notag \\
&=\frac{2rx}{r+l}\tan \theta
.\end{align}
根据光程差判据
\begin{align}
&\Delta l=m \lambda\notag \\
&x=\frac{r+l}{2r}\frac{\lambda}{\tan \theta }m\\
&\Delta x=\frac{r+l}{2r}\frac{\lambda}{\tan \theta }\\
&\theta =\arctan \frac{(r+l)\lambda }{2r \Delta x}\notag
.\end{align}
根据干涉极大的条件
\begin{align}
x&=\frac{r+l}{2r}\frac{\lambda}{\tan \theta }(N+1)\notag \\
x&=\frac{r+l}{2r}\frac{\lambda+\Delta \lambda }{\tan \theta }N\notag\\
N&=\frac{\lambda}{\Delta \lambda }
.\end{align}
经过点\(O\)的光波形成干涉条纹的边界
\begin{align}
x&=2l \tan \theta \notag \\
N&=\frac{x}{\Delta x}
.\end{align}
\hspace{2em} 2.设光源向上偏移\(\updelta s\)，引起成像点偏移\(\updelta x\)（\(\updelta x>0\)则向上，反之则向下），考虑镜面上反射点不变，镜面左侧光程差为\(\Delta l_1\)，右侧为\(\Delta l_2\)，设两个反射点间距为\(d\)，经过一顿近似
\begin{align*}
&\Delta l_1\doteq d \sin \psi \doteq d \psi \\
&\psi \doteq \tan \psi =\frac{\updelta s}{r_1}\doteq \frac{d}{r_2} \\
&r_1\doteq \frac{\updelta s}{\psi },\quad r_2\doteq \frac{d}{\psi }\\
&r\doteq \frac{\updelta s+d}{\psi }\\
&\psi \doteq \frac{\updelta s+d}{r} .
\end{align*}
可以算出
\begin{align}
\Delta l_1&\doteq d\cdot \frac{\updelta s+d}{r}\doteq \frac{d}{r}\updelta s, \\
\Delta l_2&\doteq \frac{d}{l}\updelta x
.\end{align}
从而
\begin{align}
\updelta x&=-\frac{l}{r}\updelta s \notag \\
\updelta x&=\frac{1}{2}\Delta x=\frac{(r+l)\lambda}{4r\tan \theta }\notag\\
b_c&=2\updelta s =\frac{(r+l)\lambda}{4l\tan \theta }
.\end{align}

\newpage
\subsection{薄膜干涉}
设薄膜两表面近似平行、折射率为\(n\)，置于折射率为\(n_1\)的介质中，\(\theta_i,\theta_r \)是入射光在薄膜上表面的入射角、折射角，则在定域中心处交叠的两束光的光程差为
\begin{align}
\Delta l=2nt\cos \theta _r+\frac{\lambda}{2}.
\end{align}
推导中用到了薄膜的上下表面近似平行的条件，因此该公式可以用于求平行薄膜干涉的定域中心的光程差，也可用于求厚度不均匀但是起伏较小的薄膜干涉的定域中心的光程差。\\
\phantom{awd}\par
式中\(\lambda /2\)是两束相干光在性质不同的介质界面上反射而引起的\textbf{半波损失}。若\(n>n_1\)，则沿入射光的方向，上表面从光疏介质到光密介质，下表面性质相反，实验和理论都说明，当光在性质相反的界面上反射时，两束反射光之间会产生大小为\(\pi\)的相位差，相当于大小为\(\lambda /2\)的光程差。\\
注意，半波损失是相对的，只有当两束反射光相比较时才可以说有这个\(\lambda /2\)的光程差。本文约定，从光疏-光密介质界面上反射的光比从光密-光疏介质界面上反射的光少走\(\lambda /2\)的光程，相当于“损失了半个波长”。\\
对于一定波长\(\lambda \)的单色光，光程差\(\Delta l\)是\(n,t,\theta _i\)的多元函数，分别固定变量就是以下两种理论简单而应用广泛的情况。
\subsubsection{等倾干涉}
对于等厚度的均匀薄膜（\(n,t\)为常数），光程差取决于入射光在薄膜上的入射角\(\theta_i \)，因此相同入射角的光形成的两束反射光在相交区有相同的光程差，从而属于同一级干涉条纹，故称等倾干涉。\\
等倾干涉的圆环形干涉条纹的半径大小可以由相应的入射角求出，从而测量圆环干涉条纹的半径就可以知道相应的入射角、光程差。\\
由光程差判据
\begin{align}
2nt\cos \theta _r+\frac{\lambda}{2}=
\begin{cases}
m \lambda ,\\
\left( m+\frac{1}{2}\right)\lambda .
\end{cases}
\end{align}
可以看出当\(\theta _r\)为零时\(m\)值最大，所以中心点的干涉级数最大，边缘的干涉级数较小。\\
设中心点恰为亮点，级数为\(m_0\)
\begin{align*}
2nt+\frac{\lambda}{2}=m_0\lambda ,
\end{align*}
从中心点向外数第\(N\)个亮环的级数设为\(m=m_0-N\)
\begin{align*}
2nt\cos \theta _{rm}+\frac{\lambda}{2}=m \lambda ,
\end{align*}
在观察范围很小（傍轴近似）的情况下\(\theta _r\)为小量，有近似
\begin{align*}
\cos \theta _{rm}&\doteq1-\frac{1}{2}\theta _{rm}^2,\\
n_1\theta _{im}&\doteq n \theta _{rm},
\end{align*}
代入得到
\begin{align}
&2nt(1-\cos \theta _{rm})=N \lambda\notag \\
&\theta _{rm}^2=\frac{N \lambda }{nt}\notag\\
&\theta _N=\theta _{i m}=\frac{1}{n_1}\sqrt{\frac{nN \lambda }{t}} .
\end{align}
式中\(\theta _{i m}\)是\(m\)级亮环对应的入射角，也是该亮环的角半径。\\
对上式求微分并令\(\Delta N=1\)，得到第\(N\)个条纹附近相邻两圆环的角间距
\begin{align}
\Delta \theta _N&=\frac{1}{2n_1}\sqrt{\frac{n \lambda }{Nt}}\Delta N
=\frac{\theta_N}{2N}\Delta N,\notag\\
&=\frac{\theta_N}{2}\frac{n \lambda }{\theta _N^2n_1^2t}\Delta N
=\frac{n \lambda }{2n_1^2t \theta _N}
.\end{align}
设\(f\)为透镜的焦距，（傍轴近似下）圆环干涉条纹的半径和条纹间距为
\begin{align*}
\begin{cases}
r_N=f \theta _N=\frac{f\sqrt{nN \lambda /t} }{n_1},\\
\Delta r_N=f \Delta \theta _N=\frac{nf \lambda }{2n_1^2t \theta _N}.
\end{cases}
\end{align*}
上式说明条纹半径越大，级数越小，条纹间距也越小，所以等倾干涉圆环条纹的特征是中央稀疏而边缘密集，级数从中心向外递减。

\subsubsection{等厚干涉：楔形薄膜}
令单色平行光垂直地入射厚度不均匀的薄膜（\(n,\theta_i \)为常数），此时光程差只依赖于薄膜的厚度\(t\)，因此同级干涉条纹与薄膜的等厚线对应，故称等厚干涉。\\
光程差为
\begin{align}
\Delta l=2nt+\frac{\lambda}{2}.
\end{align}
据光程差判据
\begin{align}
2nt+\frac{\lambda}{2}=
\begin{cases}
m \lambda,\\
\left( m+\frac{1}{2} \right) \lambda .
\end{cases}
\end{align}
对于楔形薄膜，其等厚干涉条纹是一系列与棱边平行的明暗相间的直条纹。\\
易知\(m\)级亮纹处楔形薄膜的厚度为
\begin{align}
t_m=\frac{(m-1/2)\lambda }{2n}.
\end{align}
其与相隔\(N\)级的亮纹的薄膜厚度差为
\begin{align*}
\Delta t=N\lambda /2n,
\end{align*}
设楔形薄膜的尖角\(\alpha \)很小，则这两条亮纹的间距
\begin{align}
&\Delta x\sin \alpha =\Delta t,\notag\\
&\Delta x=\frac{N\lambda}{2n \sin \alpha} \thickapprox \frac{N\lambda}{2n \alpha} .
\end{align}
那么若已知所用波长和薄膜的折射率，通过测量条纹间距就可以计算薄膜的尖角\(\alpha \)。
\newpage
\subsubsection{例题：增透膜和增反膜}
在光学元件表面镀一层介质薄膜可以增加其透射率或反射率。若光学元件的折射率为\(n_2\)，在其表面镀一层折射率为\(n\)的介质膜，膜上方的介质折射率为\(n_1\)，且\(n_1<n<n_2\)，要得到增透膜，就要求入射光在薄膜上下表面反射光的光程差满足干涉极小，这样反射光能量就相互抵消减弱，导致透射光能量增强。\\
设光垂直入射，因为\(n_1<n<n_2\)，没有半波损失，光程差
\begin{align}
\begin{cases}
\Delta l=2nt,\\
\Delta l=\left( m+\frac{1}{2} \right)\lambda,
\end{cases}
\end{align}
因此增透膜的厚度为
\begin{align*}
t=\frac{(m+1 /2)\lambda }{2n}.
\end{align*}
若换为折射率\(n'\)、厚度相等的介质膜，且\(n'>n_1,n_2\)，则有半波损失
\begin{align}
\begin{cases}
\Delta l=2nt+\frac{\lambda}{2},\\[2pt]
2nt=\left( \,m+\frac{1}{2} \,\right)\lambda,
\end{cases}
\end{align}
解得光程差
\begin{align*}
\Delta l=(m+1)\lambda .
\end{align*}
满足干涉极大，反射光能量相互增强，这就得到了增反膜。
\subsubsection{等厚干涉：Newton环}
在一块平板玻璃上放一个凸面向下、曲率半径\(R\)很大的平凸透镜，透镜与平板玻璃间形成很薄的、厚度不均匀的空气层，这就是Newton环装置。令单色光垂直入射，然后在空气层的两个表面反射而产生等厚干涉。这时两束相干光的光程差为（空气折射率\(n\thickapprox 1\)）
\begin{align}
\Delta l=2t-\frac{\lambda}{2}.
\end{align}
空气薄膜的等厚线是以接触点\(O\)为中心的同心圆，所以干涉条纹也是一组以\(O\)为中心的同心圆，即Newton环。如果透镜与平板接触良好，那么在\(O\)点的空气层厚度为零，从而\(\Delta l\,\Big |_O=-\frac{\lambda}{2}\)，\(O\)点是暗点。\\
今求\(m\)级亮环的半径\(r_m\)，设\(m\)级亮环处空气层厚度为\(t_m\)，则由光程差判据
\begin{align*}
&2t_m-\frac{\lambda}{2}=m \lambda ,\\
&t_m=\frac{(m+1 /2)\lambda }{2} ,
\end{align*}
由几何关系易知
\begin{align}
r_m^2=R^2-(R-t_m)^2=2R t_m-t_m^2\thickapprox 2Rt_m,
\end{align}
代入得到
\begin{align}
&t_m=r_m^2 /2R,\notag\\
&r_m=\sqrt{(m+1 /2)R \lambda } .
\end{align}
同理\(m\)级暗环的半径
\begin{align}
r_m'=\sqrt{mR \lambda }.
\end{align}
由上述半径的表达式可知，干涉条纹圆环的半径越大，干涉级数越大，空气层上下两面的夹角越大，因而条纹越密。\\
利用上式可以测量透镜的曲率半径，设\(m\)级和\(m+N\)级暗环的半径满足
\begin{align*}
\begin{cases}
r_m'=\sqrt{mR \lambda} ,\\
r_{m+N}'=\sqrt{(m+N)R \lambda} ,
\end{cases}
\end{align*}
整理得
\begin{align}
R=\frac{r_{m+N}^2-r_m^2}{N \lambda }.
\end{align}
因此已知波长，只需测出任两级暗环的半径、数出级数差，就可以计算透镜的曲率半径。反过来，已知透镜的曲率半径，就可以计算波长。\\
\paragraph{变式}
\begin{enumerate}
\item 用彼此凸面紧贴的两平凸透镜观察牛顿环，两平凸透镜曲率半径分别为\(R_1,\,R_2\)，计算\(m_1\)级暗环的半径；
\item 凸面曲率半径为\(R_1\)的平凸透镜，凸面放在凹透镜凹面上，凹面曲率半径为\(R_2\)，计算\(m_2\)级暗环的半径。
\end{enumerate}
\textbf{解}\quad 1.设\(t_1,\,t_2\)分别为\(m_1\)级暗环处两平凸透镜相对相切平面的空气层厚度，\(r\)为\(m_1\)级暗环的半径，由几何关系
\begin{align}
&r^2=R_1^2-(R_1-t_1)^2\thickapprox 2R_1t_1,\notag\\
&r^2\thickapprox 2R_2t_2,\notag\\
&t=t_1+t_2=\frac{r^2}{2}\left( \frac{1}{R_1}+\frac{1}{R_2} \right).
\end{align}
且光程差满足
\begin{align}
\begin{cases}
\Delta l=2t-\frac{\lambda}{2},\\
\Delta l= \left( m+\frac{1}{2} \right) \lambda,
\end{cases}
\end{align}
解得
\begin{align}
r=\sqrt{\frac{R_1R_2(m+1)\lambda }{R_2+R_1}} .
\end{align}
\hspace{2em}2.同理设\(t_1,\,t_2\)分别为\(m_2\)级暗环凸透镜、凹透镜相对相切平面的空气层厚度，\(r\)为\(m_2 \)级暗环的半径，由几何关系易知
\begin{align}
&r^2\thickapprox 2R_1t_1,\notag\\
&r^2\thickapprox 2R_2t_2,\notag\\
&t=t_1-t_2=\frac{r^2}{2}\left( \frac{1}{R_1}-\frac{1}{R_2} \right) .
\end{align}
光程差满足
\begin{align*}
\begin{cases}
\Delta l=2t-\frac{\lambda}{2},\\
\Delta l=\left( m+\frac{1}{2} \right)\lambda ,
\end{cases}
\end{align*}
解得
\begin{align}
r=\sqrt{\frac{R_1R_2(m+1)\lambda }{R_2-R_1}} .
\end{align}
\paragraph{注}
\begin{enumerate}
\item 在薄膜干涉中不用单色光，而用白光会怎样？ \\
此时将出现彩色的干涉条纹，只有前几级，且条纹变宽、变模糊。\\
这是因为相位差\(\delta =2\pi \Delta l /\lambda \)与\(\lambda \)有关，以楔形薄膜为例，已知
\begin{align*}
t_m&=\frac{(m-1/2)\lambda }{2n},\\
\Delta x&=\frac{N\lambda}{2n \sin \alpha}.
\end{align*}
可以看出波长越长，\(m\)级条纹处膜厚度\(t_m\)越大，条纹间距\(\Delta x\)越大，所以各色光的条纹相互错开，而且随着厚度\(t\)增加，不同波长的同级条纹错开得越厉害，所以除了厚度较小的区域能观察到彩色的条纹外，其他地方的条纹已经融成一片，无法分辨。在肥皂膜和水面的油膜上常常可以看到这种彩色条纹。
\item 透射光是否也和反射光一样有这样的干涉？\\
两束透过薄膜的透射光也是相干光，当薄膜两侧的介质相同时，两束透射光的光程差为
\begin{align}
\Delta l=2nt \cos \theta _r.
\end{align}
与反射光的光程差相比，只相差\(\lambda /2\)，即相位差\(\pi\)，因此当某一入射角的反射光干涉条纹是亮纹时，透射光干涉条纹是暗纹，二者互补。
\item 薄膜厚度很大时，是否还能看到干涉条纹？\\
因为实际入射光不是单色光，而是有一波长范围\((\lambda ,\, \lambda +\Delta \lambda )\)，干涉条纹的最大相干光程差是\(\Delta l_M=\frac{\lambda^2}{\Delta \lambda } \)，如果薄膜太厚，上下表面反射光的光程差就很大，光程差超过最大光程差时，干涉条纹就不可分辨了。
\end{enumerate}
\newpage
\subsection{Michelson干涉仪}
\subsubsection{精确测量波长}
Michelson干涉仪分出的两束光的光程差，与以一反射镜和另一反射镜的虚像为上下表面的空气薄膜的光程差相同，故等效于空气薄膜的干涉。当二镜面严格垂直时，出现等倾条纹；当二镜面不严格垂直时，出现近似平行的等厚条纹。\\
由薄膜干涉的光程差，注意到\(\theta _i=\theta _r\)，有
\begin{align}
\Delta l=2t\cos\theta_i.
\end{align}
代入光程差判据，等倾干涉条纹的第\(m\)级亮环满足
\begin{align*}
2t\cos\theta_i=m\lambda.
\end{align*}
因此越靠近圆心的亮环，级数越大，圆心处干涉级数最大
\begin{align*}
m_{\max}=2t /\lambda ,
\end{align*}
可知，\(t\)增大半个波长，\(m_{\max}\)增大一个数目，实验中观察到干涉条纹从中心吐出一个亮环。数出增加的亮环数目\(N\)，就可以算出反射镜平移的距离
\begin{align}
\Delta t=N \lambda /2.
\end{align}
根据上式，已知入射光的波长，可以精确测量长度；反过来，可以通过测量平移的距离来测量波长。
\subsubsection{精确测量波长差}
波长十分接近的两条光谱会形成双线结构，以之入射，设两谱线光强相等，Michelson干涉仪的两臂光强均为\(I_0 /2\)，每条谱线产生的干涉光强分布是
\begin{align}
I_i(\Delta l)=I_0[1+\cos(k_i\Delta l)],\quad k_i=2\pi /\lambda_i.
\end{align}
则总光强是它们的非相干叠加
\begin{align}
I(\Delta l)&=I_1(\Delta l)+I_2(\Delta l)\notag\\
&=I_0[2+\cos(k_1\Delta l)+\cos(k_2\Delta l)]\notag\\
&=2I_0\left[ 1+\cos \left(\frac{\Delta k}{2}\Delta l\right) \cos(\bar k\Delta l)\right] .
\end{align}
由于
\begin{align*}
\Delta k&=\frac{2\pi}{\lambda_1}-\frac{2\pi}{\lambda_2},\\
&\doteq \frac{2\pi\Delta\lambda}{\bar \lambda ^2}.
\end{align*}
\(\Delta \lambda \)很小，故\(\Delta k\)很小，从而\(\Delta l\)的变化可近似为不变，可得反衬度
\begin{align}
\gamma (\Delta l)=\bigg |\cos \left( \frac{\Delta k}{2}\Delta l \right) \bigg |.
\end{align}
因此当双线光谱入射Michelson干涉仪时，干涉条纹的反衬度随光程差的变化作周期性的变化。将反射镜平移时，光程差变化，反衬度时大时小。
\newpage
实验中，为了测量微小的波长差，可以先调整反射镜得到一个清晰的干涉图样，此时光程差为\(\Delta l_1\)，再持续沿着同一方向平移反射镜直到条纹又变得清晰，此时光程差为\(\Delta l_2\)，显然反射镜平移的距离就是空气层厚度的改变量\(\Delta t\)，满足\(\Delta l_2-\Delta l_1=2\Delta t\)。\\
因为\(\Delta l_1,\,\Delta l_2\)是相邻两次使得干涉条纹最清晰的光程差，即反衬度为\(1\)，代入上式
\begin{align*}
\begin{cases}
\Delta k\Delta l_1 /2=m\pi,\\
\Delta k\Delta l_2 /2=(m+1)\pi.
\end{cases}
\end{align*}
从而
\begin{align}
\Delta t&=\frac{\pi}{\Delta k},\notag\\
&\doteq\frac{\pi}{2\pi\frac{\Delta \lambda}{\bar\lambda^2}}=\frac{\bar\lambda^2}{2\Delta\lambda}.
\end{align}
只要测出\(\Delta t,\,\bar\lambda\)，就可以算出波长差\(\Delta \lambda \)。这里\(\Delta t\)也可以是使得干涉条纹相继两次反衬度最小的反射镜平移距离。
\subsubsection{光源的非单色性和时间相干性}
原子的发光时间称作\textbf{相干时间}，由同一光源在相干时间\(\tau_0\)内不同时刻发出的光，经过不同路径到达干涉场将产生干涉，反之则不会产生干涉，光的这种特性称为\textbf{时间相干性}。\\
相干时间内光源发出的波列长度称作\textbf{相干长度}，从而相干长度\(l_c=c\tau_0\)，当从同一光源分出的两束光的光程差\(\Delta l\leqslant l_c\)时，两束光部分或全部来自同一波列，从而发生干涉，反之两束光完全来自不同的波列，不会产生干涉。\\
\phantom{awd}\par
下面以Michelson干涉仪为例，讨论光源的非单色性对干涉条纹反衬度的影响。\\
设光源的波数范围为\(\Delta k\)，且各波数的光强相等，因此元波数宽度\(\mathrm dk\)在干涉仪中产生的光强分布为
\begin{align*}
\mathrm dI=2I_0[1+\cos(k\Delta l)]\,\mathrm dk.
\end{align*}
其中\(I_0\)代表光强的谱密度。\\
不同光谱成分不相干，总光强
\begin{align}
I=\int_{k_0-\Delta k /2}^{k_0+\Delta k /2}2I_0[1+\cos(k\Delta l)]\,\mathrm dk=2I_0\Delta k \left[ 1+\frac{\sin(\Delta k\Delta l /2)}{\Delta k\Delta l /2} \cos(k_0\Delta l)\right] .
\end{align}
上式第一项是常数，代表干涉场的平均光强；第二项随光程差增大而变化，但变化幅度越来越小。\\
由此可以得到反衬度为
\begin{align}
\gamma (\Delta l)=\bigg |\frac{\sin(\Delta k\Delta l /2)}{\Delta k\Delta l /2}\bigg |.
\end{align}
这意味着当\(\Delta l\)从\(0\)增大到最大值
\begin{align}
\Delta l_{\max}=\frac{2\pi}{\Delta k}=\frac{\lambda ^2}{\Delta \lambda }
\end{align}
时，反衬度单调下降至\(0\)，该结果验证了由Young's双缝干涉计算得到的最大光程差。\\
实际上，之所以光源的非单色性使得反衬度单调下降，是因为\(\Delta \lambda \)范围内每一种波长的光都生成一组干涉条纹，各组条纹除零级条纹外相互都有位移，各组条纹交错重叠，发生非相干叠加。

\subsubsection{例题：覆水膜的Michelson干涉仪}
用Michelson干涉仪做实验时，开始时在补偿片一侧有一层水膜，水膜逐渐蒸发过程中，观察到移动了\(N\)个条纹。设入射光的波长是\(\lambda \)，空气折射率为\(1\)，水的折射率为\(n\)，光线关于补偿片的入射角为\(\theta \)，求水膜的厚度\(t\)。
\paragraph{解}\quad 设折射角为\(\psi \)，由Snell定律
\begin{align*}
\sin\theta=n\sin\psi,
\end{align*}
由几何关系易知，实验开始时的光程差为
\begin{align}
\Delta l_1=2t\cos\theta+\frac{2nt}{\cos\psi}+2t \left[ \frac{1}{\cos\theta}-\frac{\cos(\theta -\psi )}{\cos\psi} \right] .
\end{align}
考虑第\(m\)级亮环的上一点\(p\)
\begin{align*}
\Delta l_1=m\lambda.
\end{align*}
水膜完全蒸发后光程差为
\begin{align}
\Delta l_2=2t\cos\theta+\frac{2t}{\cos\theta}.
\end{align}
因而点\(p\)处
\begin{align*}
\Delta l_2=(m-N)\lambda.
\end{align*}
从而
\begin{align}
t&=\frac{N\lambda\cos\psi}{2[n-\cos(\theta -\psi )]},\notag\\
&=\frac{N\lambda\sqrt{n^2-\sin^2\theta } }{2\left(n^2-\sin^2\theta -\cos\theta\sqrt{n^2-\sin^2\theta } \right)}.
\end{align}

\newpage
\subsection{薄膜的多光束干涉}
这里多光束干涉指一组彼此平行，任意相邻两束光的光程差相同的光束的相干叠加。
\subsubsection{多光束干涉的光强分布}
实际上，在光照射薄膜的情况下，得到的反射光就是多光束。因为入射光在薄膜上下表面之间经过多次反射透射，所以反射光有很多条。但是每反射/透射一次，光就被分成两部分，每一部分都比原来弱，于是反射光逐渐减弱。因此在讨论薄膜干涉问题时，近似地只考虑了第1,\,2条反射光的干涉。若上下表面的反射系数足够大，就能得到光强适当大且彼此接近的多光束。\\
具体地，设光束入射薄膜时，反射系数为\(r\)、透射系数为\(t\)，从薄膜射出时系数为\(r',\,t'\)，入射光的振幅为\(A\)，则反射光的振幅依次为
\begin{align*}
Ar,\,Att'r',\,Att'r'^3,\,Att'r'^5,\cdots,\,Att'r'^{2n-3},\,\cdots
\end{align*}
透射光的振幅依次为
\begin{align*}
Att',\,Att'r'^2,\,Att'r'^4,\,Att'r'^6,\cdots,\,Att'r'^{2n-2},\,\cdots
\end{align*}
在薄膜的上下表面平行的情况下，上述两系列光束中每对相邻光线之间的光程差都相等。不考虑半波损失（实际上只有第1,\,2条反射光线有半波损失），相邻两条光线的相位差为
\begin{align}
\delta=\frac{2\pi}{\lambda }\,\Delta l=\frac{2\pi}{\lambda }\cdot 2nt\cos\theta_r=\frac{4\pi nt\cos\theta_r}{\lambda }.
\end{align}
从而反射光的复振幅
\begin{align}
\tilde E_1&=Ar,\notag\\
\tilde E_2&=Att'r'\mathrm e^{\mathrm i\delta},\notag\\
\tilde E_3&=Att'r'^3\mathrm e^{2\mathrm i\delta},\notag\\
&\cdots\notag\\
\tilde E_n&=Att'r'^{2n-3}\mathrm e^{(n-1)\mathrm i\delta},\\
&\cdots\notag
\end{align}
透射光的复振幅
\begin{align}
\tilde E_1'&=Att',\notag\\
\tilde E_2'&=Att'r'^2\mathrm e^{\mathrm i\delta},\notag\\
\tilde E_3'&=Att'r'^4\mathrm e^{2\mathrm i\delta},\notag\\
&\cdots\notag\\
\tilde E_n'&=Att'r'^{2n-2}\mathrm e^{(n-1)\mathrm i\delta},\\
&\cdots\notag
\end{align}
二者的总振幅和总光强为
\begin{align*}
\begin{cases}
\tilde E_R=\sum_{n=1}^\infty\tilde E_n,\\
\tilde E_T=\sum_{n=1}^\infty\tilde E_n'.
\end{cases}\quad
\begin{cases}
I_R=\tilde E_R\tilde E_R^*,\\
I_T=\tilde E_T\tilde E_T^*.
\end{cases}
\end{align*}
根据等比级数的求和
\begin{align}
\tilde E_T=\sum_{n=1}^\infty Att'(r'^2\mathrm e^{\mathrm i\delta})^{n-1}=\frac{Att'}{1-r'^2\mathrm e^{\mathrm i\delta}}.
\end{align}
因此
\begin{align*}
I_T&=\frac{Att'}{1-r'^2\mathrm e^{\mathrm i\delta}}\cdot\frac{Att'}{1-r'^2\mathrm e^{-\mathrm i\delta}},\notag\\
&=\frac{A^2(t t')^2}{1-r'^2(\mathrm e^{\mathrm i\delta}+\mathrm e^{-\mathrm i\delta})+r'^4}
=\frac{I_0(tt')^2}{1-2r'^2\cos\delta+r'^4}.
\end{align*}
这里\(I_0=A^2\)是入射光的光强。\\
由Stokes倒逆关系
\begin{align}
\begin{cases}
r=-r',\\
r^2+t t'=1.
\end{cases}
\end{align}
代入得到
\begin{align*}
I_T=\frac{I_0(1-r^2)^2}{1-2r^2\cos\delta+r^4}.
\end{align*}
设反射率\(R=r^2\)、精细度系数\(F=\frac{4R}{(1-R)^2}\)，则透射光强又可写为
\begin{align}
I_T&=\frac{I_0(1-R)^2}{1-2R\cos\delta+R^2}
=\frac{I_0}{\frac{1+4R\sin^2(\delta /2)-2R +R^2}{(1-R)^2}},\notag\\
&=\frac{I_0}{1+\frac{4R\sin^2(\delta /2)}{(1-R)^2}}
=\frac{I_0}{1+F\sin^2(\delta /2)}.
\end{align}
根据光强守恒\(I_R+I_T=I_0\)，反射光强
\begin{align}
I_R=\frac{I_0}{1+1 /[F\sin^2(\delta /2)]}.
\end{align}
对于固定的\(R\)，\(I_T,\,I_R\)随\(\delta \)的变化而变化，又\(\delta =4\pi nt\cos\theta_r /\lambda \)，从而单色光入射的总光强只与倾角\(\theta _r\)有关，于是薄膜的多光束干涉是\textbf{多光束等倾干涉}。\\
根据光强分布公式，当\(\delta =2m\pi\)时，\(I_R\)极小，\(I_T\)极大，因此二者的干涉图样互补。

\newpage
\subsubsection{干涉条纹的锐度}
比较不同\(R\)值下的\(I_T-\delta\)曲线可以看出，当\(R\)增大时，透射光的光强分布曲线变得越来越陡。这是因为\(R\)增大使无穷级数中后面的光束变强，从而参与干涉效应的光束数目变大，所以干涉条纹的锐度变大，这是多光束干涉最重要的特征。\\
干涉条纹的锐度由条纹的\textbf{相位差半值宽度}\(\Delta \delta \)描述，它是指条纹中强度为峰值一半的两点的相位差。\\
对于第\(m\)级亮纹，两个半值强度点为
\begin{align*}
\delta =2m\pi\pm \frac{\Delta \delta }{2},
\end{align*}
依定义代入透射光强
\begin{align*}
\frac{I_0}{1+F\sin^2(\Delta \delta /4)}=\frac{I_0}{2},
\end{align*}
由\(\Delta \delta \)很小，近似取\(\sin(\Delta \delta /4)\doteq \Delta \delta /4\)，代入得到
\begin{align}
\Delta \delta =\frac{4}{\sqrt{F} }=\frac{2(1-R)}{\sqrt{R} }.
\end{align}
于是\(R\rightarrow 1\)时\(\Delta \delta \rightarrow 0\)，干涉条纹变得极细，而精细度系数\(F\rightarrow \infty\)。\\
\phantom{awd}\par
虽然相位差半值宽度衡量了条纹的锐度，但它是一个相位值，难以直接测量，回忆起对于以单色光入射的多光束干涉装置，影响相位差\(\delta =4\pi nt\cos\theta_r /\lambda \)的只有倾角\(\theta _r\)，从而可以通过测量倾角的变化量说明条纹的锐度。\\
设\(\theta _{rm}\)为第\(m\)级亮纹的角位置，使得\(\delta\)变化到半值强度点的倾角范围\(\Delta \theta _r\)称为\textbf{干涉条纹半角宽}。\\
固定\(n,\,t,\,\lambda \)对\(\delta \)取关于\(\theta _r\)的微分
\begin{align*}
\mathrm d\delta=-\frac{4\pi nt\sin\theta_r}{\lambda }\,\mathrm d\theta_r ,
\end{align*}
令\(\mathrm d\delta=\Delta\delta=2(1-R) /\sqrt{R} \)，将\(\mathrm d\theta_r\)写成\(\Delta\theta_{rm}\)，得
\begin{align}
\Delta \theta _{rm}=\frac{\lambda (1-R)}{2\pi nt\sin\theta_r\sqrt{R} }.
\end{align}
可以看出当反射率\(R\)（同时精细度系数\(F\)）或间隔\(t\)增大时，条纹变得更细锐。

\newpage
\subsubsection{Fabry-Perot干涉仪的角色散本领和色分辨本领}
\textbf{角色散本领}描述干涉仪将不同谱线分开的能力，设两光波的波长为\(\lambda,\,\lambda+\updelta\lambda\)，它们的\(m\)级亮纹之间的角距离为\(\updelta\theta\)，则角色散本领定义为
\begin{align}
\mathscr D=\frac{\updelta\theta}{\updelta\lambda}.
\end{align}
即将波长相差一个单位的两谱线分开的角距离。\\
两光波的第\(m\)级亮纹的角位置分别满足
\begin{align*}
\begin{cases}
2nt\cos\theta_{rm}=m\lambda,\\
2nt\cos\theta_{rm}'=m(\lambda +\updelta \lambda ),
\end{cases}
\end{align*}
当\(\theta _{rm}\)和\(\theta _{rm}'\)很接近时
\begin{align*}
\cos\theta_{rm}'-\cos\theta_{rm}\doteq\sin\theta_{rm}\updelta\theta_{rm}
\end{align*}
代入得到
\begin{align}
&2nt(\cos\theta_{rm}'-\cos\theta_{rm})=m\updelta\lambda,\notag\\
&\mathscr D=\frac{\updelta\theta_{rm}}{\updelta \lambda }=\frac{m}{2nt\sin\theta_{rm}}.
\end{align}
可知，当干涉级数\(m\)增大或间隔\(t\)减小时，两谱线的角色散也增大。\\
\phantom{awd}\par
\textbf{色分辨本领}描述干涉仪分辨谱线的能力，设干涉仪对波长在\(\lambda \)附近能够分辨的最小波长差为\(\updelta\lambda\)，则色分辨本领定义为
\begin{align}
\mathscr R=\frac{\lambda}{\updelta\lambda}.
\end{align}
角色散本领并不等同于色分辨本领，前者只给出两谱线分离的程度，不能说明它们是否能被分辨，因为能否分辨还取决于谱线的粗细。而根据Taylor判据，两条谱线可分辨的最小角距离正是谱线的半角宽，从而可以利用半角宽和角色散本领计算出可分辨的最小波长差。\\
令\(\Delta \theta _{rm}=\updelta \theta _{rm}\)得到可分辨的最小波长差为
\begin{align*}
\updelta \lambda =\frac{\lambda}{\pi m}\frac{1-R}{\sqrt{R} },
\end{align*}
于是
\begin{align}
\mathscr R=\frac{\uplambda}{\delta \lambda }=\frac{1}{2}\pi m\sqrt{F}.
\end{align}
因此干涉级数越大，色分辨本领越大。
\newpage
\subsubsection{Fabry-Perot干涉仪的透射光谱}
若入射Fabry-Perot干涉仪的光是连续光谱，经过多光束干涉后，只有满足透射光干涉极强的波长的光波才能穿过Fabry-Perot干涉仪，其他的光都被反射，因此Fabry-Perot干涉仪的透射光谱是谱宽很小的分立光谱，具有很强的单色性。\\
由透射光光强分布公式可知，当\(\delta=2m\pi\)时透射光为干涉极强，在正入射（\(\theta_r=0\)）时，透射波长\(\lambda_m\)满足
\begin{align}
&\delta=\frac{4\pi nt}{\lambda_m}=2m\pi,\notag\\
&\lambda_m=\frac{2nt}{m},\quad\nu _m=\frac{c}{\lambda_m}=\frac{mc}{2nt}.
\end{align}
透射光的每条谱线\(\lambda_m /\nu_m\)称为一个纵模，对一个Fabry-Perot干涉仪来说可以有无穷多个纵模。\\
纵模的间隔为
\begin{align}
\Delta\nu=\frac{c}{2nt}.
\end{align}
可知，相邻干涉极强光的频率间隔都相等，与干涉级数\(m\)无关，但与\(t\)成反比。\\
透射光的频率/波长范围称作纵模宽度。当非单色平行光正入射Fabry-Perot干涉仪时，相位差仅由波长决定，即\(\delta=4\pi nt /\lambda \)，对\(\delta\)取关于\(\lambda\)的微分
\begin{align*}
\mathrm d\delta=-\frac{4\pi nt}{\lambda^2}\,\mathrm d\lambda,
\end{align*}
令\(\mathrm d\delta=\Delta\delta=2(1-R) /\sqrt{R} \)，把\(\mathrm d\lambda\)写成\(\Delta\lambda\)，得
\begin{align}
\Delta\lambda=\frac{\lambda ^2(1-R)}{2\pi nts\sqrt{R} },\quad\Delta\nu=\frac{c\Delta\lambda}{\lambda^2}=\frac{c(1-R)}{2\pi nt\sqrt{R} }.
\end{align}
因此反射率\(R\)越大，或腔长\(t\)越长，透射光的单色性越好。













\newpage
\section{光的衍射}
Huygens-Fresnel原理认为，波阵面\(\Sigma\)上每个面元\(\mathrm d\Sigma\)都是新的振动中心，它们发出次光波，在空间中某点\(P\)的光振动是所有这些次光波在该点的相干叠加。设\(\mathrm d\tilde E(P)\)是面元\(\mathrm d\Sigma \)在场点\(P\)产生的光矢量的复振幅，则点\(P\)处的总光振动为
\begin{align*}
\tilde E(P)=\iint_{\Sigma}\mathrm d\tilde E(P).
\end{align*}
Fresnel指出，\(\mathrm d\tilde E(p)\)的大小正比于以下四个物理量，可以称之为\textbf{复振幅四要素}：
\begin{enumerate}
\item \textbf{面积}：面元的面积\(\mathrm d\Sigma\)；
\item \textbf{振幅}：面元上点\(Q\)的光矢量的振幅\(E_0(Q)\)；
\item \textbf{光程}：球面波因子\(\exp(\mathrm ikr)/r\)；
\item \textbf{倾角}：面元法线\(n\)和面元到场点的连线\(r\)的夹角\(\theta \)，面元法线\(n\)和面元到光源的连线\(R\)的夹角\(\theta_0 \)。
\end{enumerate}
Kirchhoff从光矢量的波动方程出发，根据矢量分析，建立了光衍射的严格理论，他认为光衍射的系统可以分为三个部分：衍射屏的光孔\(\Sigma_0\)，衍射屏的不透光部分、无限大平面\(\Sigma_1\)、半径为无限大的半球面\(\Sigma_2\)，还假设\(\Sigma_0\)上的复振幅取自由传播时光场的值，而在\(\Sigma_1\)上取零，并证明了其在\(\Sigma_2\)上的积分为零，在上述Kirchhoff边界条件下，得到
\begin{align}
\tilde E(P)=\frac{-\mathrm i}{\lambda}\iint_{\Sigma_0}\frac{\cos \theta_0+\cos \theta }{2}\,E_0(Q)\,\frac{\mathrm e^{\mathrm ikr}}{r}\,\mathrm d\Sigma.
\end{align}
上式称为\textbf{Fresnel-Kirchhoff衍射积分公式}，通过计算该面积分，可以求出光衍射场中点\(P\)的光矢量大小。\\
在光孔和接收范围远小于光源\(S\)和场点\(P\)到光孔的距离，且入射光和衍射屏近似垂直（傍轴条件）下，上式化为
\begin{align}
\tilde E(P)=\frac{-\mathrm i}{\lambda r_0}\iint_{\Sigma_0}E_0(Q)\mathrm e^{\mathrm ikr}\,\mathrm d\Sigma.
\end{align}
该式在计算Fraunhofer衍射时常用。\\
\phantom{awd}\\
通常按光源、衍射屏、接收屏之间的距离，将衍射分为两类：
\begin{enumerate}
\item \textbf{Fresnel衍射（近场衍射）}
光源和观察屏至少一个离衍射屏有限远，此时入射光和衍射光至少一个不是平行光，波阵面的曲率不可忽略；
\item \textbf{Fraunhofer衍射（远场衍射）}
光源和观察屏距离衍射屏均为无限远，因此入射光和衍射光都是平行光。实验中Fraunhofer衍射必须利用两个正透镜，令点光源、接收屏分别位于两个透镜的焦点、焦平面。
\end{enumerate}

\newpage
\subsection{Fresnel圆孔衍射}
根据Huygens-Fresnel原理，计算衍射场时，一般先划分有效波阵面\(\Sigma_0\)（光孔），再计算每个面元在场点\(P\)处引起的复振幅\(\mathrm d\tilde E(P)\)，最后将所有这些复振幅相干叠加。\\
但是对于Fresnel衍射，直接积分比较困难，因此需要对有效波阵面巧妙地分割，将复杂积分转换为简单的数量或者矢量相加，下面介绍半波带法。

\subsubsection{半波带法}
设波阵面半径为\(R\)，顶点\(O\)和场点\(P\)的距离为\(b\)，在波阵面上划分出\(n\)条半波带，设第\(i\)半波带发出的次波在点\(P\)产生的复振幅为\(\tilde E_i(P)\)，相邻半波带光程差为\(\lambda /2\)，意味着相位差\(\pi\)，从而
\begin{align}
\tilde E_i(P)=E_{i0}\mathrm e^{\mathrm i[\phi_0+(n-1)\pi]},
\end{align}
于是点\(P\)处的合振幅为
\begin{align}
E_0(P)&=|\tilde E_0(P)|=\bigg |\sum_{i=1}^n \tilde E_{i}(P)\bigg |,\notag\\
&=\sum_{i=1}^n(-1)^{i-1}E_{i 0}.
\end{align}
为此比较各项，根据Huygens-Fresnel原理，可知各振幅的大小
\begin{align*}
E_{i 0}\propto f(\theta_i)E_0(Q)\,\frac{\mathrm e^{\mathrm ikr_i}}{r_i}\,\Delta\Sigma_i.
\end{align*}
由几何关系易知\(\frac{\Delta\Sigma_i}{r_i}\thickapprox \frac{\pi R\lambda}{R +b}\)与\(i\)无关，又由于球面波等相面上复振幅\(E_0(Q)\mathrm e^{\mathrm ikr_i}\)处处相同，因而影响\(E_{i 0}\)大小的只有倾角因子\(f(\theta_i)=(1+\cos\theta_i) /2\)（球面波\(\theta_0=0\)）。\\
易知\(f(\theta_i)\)随\(i\)的增大而缓慢减小，\(\theta_i\rightarrow\pi\)时，\(f(\theta_i)\rightarrow 0\)，于是有近似
\begin{align}
\begin{cases}
E_{10}\gtrsim E_{20}\gtrsim\cdots\gtrsim E_{n0},\\
E_{i 0}\thickapprox \frac{1}{2}(E_{i-1,0}+E_{i+1,0}).
\end{cases}
\end{align}
代入得到
\begin{align}
E_0(P)&=\sum_{i=1}^n (-1)^{i-1}E_{i 0},\notag\\
&=\frac{1}{2}E_{10}+(-1)^{n-1}\frac{1}{2}E_{n 0}.
\end{align}
可知，当圆孔包含奇数个半波带时，衍射图样的中心是亮点，包含偶数个时是暗点。所以要确定中心是亮点还是暗点，先要知道半波带的数目。\\
设半波带的半径为\(\rho_i\)，则有\textbf{Fresnel衍射的Gauss公式}
\begin{align}
\frac{1}{R}+\frac{1}{b}=\frac{i\lambda}{\rho_i^2}.
\end{align}
其中\(R\)是物距，\(b\)是相距。
因而半波带的数目
\begin{align*}
n=\frac{\rho^2}{\lambda}\left( \frac{1}{R}+\frac{1}{b} \right).
\end{align*}
其中\(\rho=\rho_n\)也是圆孔的半径。可以看出中心光强随\(b\)的增大周期性变明变暗。\\
对中心轴之外各点的光强，虽然难以确定半波带的数目和面积，但是由衍射装置关于中心轴的轴对称性可知衍射图样是明暗交替的同心圆环。

\subsubsection{例题：平行光的Fresnel圆孔衍射}
\begin{enumerate}
\item 已知入射光的波长为\(\lambda\)，若在中心轴上距圆孔\(r_1\)处出现一个亮点，此时圆孔面积恰好等于第一个半波带，求圆孔半径 \(\rho\)和沿中心轴向圆孔移动时第一个暗点的位置\(r_2\)；
\item 若圆孔面积为\(S\)，在中心轴上距圆孔\(r_1\)的观察屏上得一亮点，将观察屏移近圆孔，距圆孔\(r_2\)时又得相继的亮点，求光波波长；
\item 若圆孔的半径为\(\rho\)，对于距圆孔\(r\)处的点，求圆孔包含的半波带数目。
\end{enumerate}
\textbf{解}\quad 入射光为平行光因此物距\(R=\infty\)，从而Fresnel衍射的Gauss公式化为
\begin{align*}
\frac{1}{b}=\frac{i\lambda}{\rho_i^2}.
\end{align*}
\hspace{2em}1.由题意，代入Gauss公式可得
\begin{align*}
\begin{cases}
\rho&=\sqrt{r_1\lambda},\\
\rho&=\sqrt{2r_2\lambda},
\end{cases}
\Rightarrow r_2=r_1 /2.
\end{align*}
\hspace{2em}2.由几何关系
\begin{align*}
\rho=\sqrt{\frac{S}{\pi}}.
\end{align*}
由Gauss公式，注意到观察屏上有亮点意味着有奇数个半波带
\begin{align*}
\begin{cases}
\frac{1}{r_1}&=\frac{(2k+3)\lambda}{\rho^2},\\
\frac{1}{r_2}&=\frac{(2k+1)\lambda}{\rho^2},
\end{cases}
\quad k\in \mathbb Z
\end{align*}
从而
\begin{align}
\lambda =\frac{\rho^2}{2}\left( \frac{1}{r_1}-\frac{1}{r_2} \right)
=\frac{S}{2\pi}\left( \frac{1}{r_1}-\frac{1}{r_2} \right) .
\end{align}
\hspace{2em}3.直接利用Gauss公式
\begin{align*}
n=\frac{\rho ^2}{\lambda r}.
\end{align*}

\newpage
\subsection{Fraunhofer单缝衍射}
\subsubsection{单缝衍射光强的计算}
\paragraph{复数积分法}\phantom{awd}\par
设狭缝宽度为\(a\)，将狭缝内的平面波波前划分为等宽的条形\(\mathrm dx\)，由于观察屏在透镜的后焦面上，和主轴夹角\(\theta\)相同的衍射光线汇聚于屏幕上同一点\(P_\theta\)，按Fresnel-Kirchhoff-Fraunhofer衍射积分公式
\begin{align}
\tilde E_0(P_\theta)=\frac{-\mathrm i}{\lambda z_0}\iint_{\Sigma_0}E_0(Q)\mathrm e^{\mathrm ikr}\,\mathrm dx\mathrm dy.
\end{align}
其中\(r\)是波前上\(x\)处的点\(Q\)到场点\(P_\theta\)的光程，由几何关系易知它和波前上主轴处的点\(O\)到\(P_\theta\)的光程差为
\begin{align*}
\Delta r=r-r_0=-x\sin\theta,
\end{align*}
由于入射光是平行光，\(E_0(Q)\)具有相同的大小。代入计算得
\begin{align}
\tilde E_0(P_\theta)&=\frac{-\mathrm ilE_0(Q)}{\lambda z_0}\int_{-a /2}^{+a /2}\mathrm e^{\mathrm ik(r_0-x\sin\theta)}\,\mathrm dx
=\frac{-\mathrm ilE_0(Q)}{\lambda z_0}\,\mathrm e^{\mathrm ikr_0}\,\frac{\mathrm e^{\mathrm ika\sin\theta /2}-\mathrm e^{-\mathrm ika\sin\theta /2}}{\mathrm ik\sin\theta},\notag\\
&=\frac{-\mathrm ilE_0(Q)}{\lambda z_0}\,\mathrm e^{\mathrm ikr_0}\,\frac{\sin\left(\frac{ka\sin\theta}{2}\right)}{\frac{k\sin\theta}{2}}
=\frac{-\mathrm i(al)E_0(Q)}{\lambda z_0}\,\frac{\sin\alpha}{\alpha}\,\mathrm e^{\mathrm kr_0}.
\end{align}
其中\(\alpha=\frac{ka\sin\theta}{2}=\frac{\pi a\sin\theta}{\lambda}\)。\\
由计算结果的相位因子可以看出，单缝衍射光类似从单缝中心\(O\)发出的柱面波。\\
令\(\theta=0\)有
\begin{align*}
\tilde E_0(P_0)=\frac{-\mathrm i(al)E_0(Q)}{\lambda z_0}\,\mathrm e^{\mathrm ikr_0},
\end{align*}
于是
\begin{align}
\tilde E_0(P_\theta)&=\tilde E_0(P_0)\,\frac{\sin\alpha}{\alpha },\notag\\
I(P_\theta)&=I_0 \left( \frac{\sin\alpha}{\alpha} \right) ^2.
\end{align}
这就是Fraunhofer单缝衍射的光强分布公式。衍射场相对光强\((\sin\alpha /\alpha)^2\)称为\textbf{单缝衍射因子}。
\paragraph{矢量图解法}\phantom{awd}\par
首先考虑\(N\)束平行光的多光束干涉，每束光的振幅相同，任意相邻两束光具有相同的相位差\(\delta\)，求其总光强得到
\begin{align}
I=I_0 \left[ \frac{\sin(N\delta /2)}{\sin(\delta /2)} \right] ^2.
\end{align}
这里干涉场的相对光强\(\left[ \frac{\sin(N\delta /2)}{\sin(\delta /2)} \right] ^2\)称为\textbf{多光束干涉因子}。\\
回到单缝衍射，将单缝内的平面波波前均匀地分割为\(N\)条窄条，每窄条的宽度为\(\Delta x\)，窄条数\(N=a /\Delta x\)，对比复振幅四要素可知，各窄条发出的次波在\(P_\theta\)产生的复振幅相等，设为\(A\)。\\
另一方面，任意两条相邻窄条到\(P_\theta\)的光程差相等，都为\(\Delta l=\Delta x\sin\theta\)，相位差\(\delta=k\Delta x\sin\theta\)。于是\(P_\theta\)的总光强是\(N\)束相互平行、振幅相等，任意相邻两束光具有相同的相位差的次波相干叠加的结果。代入得到
\begin{align*}
I(P_\theta)=A^2\,\frac{\sin^2\left(\frac{a}{\Delta x}\,\frac{\Delta xk\sin\theta}{2}\right)}{\sin^2\left( \frac{k\Delta x\sin\theta}{2} \right) }
=A^2\,\frac{\sin^2\left(\frac{ak\sin\theta}{2}\right)}{\sin^2\left( \frac{ka\sin\theta}{2N} \right) },
\end{align*}
当分割无限细，\(N\rightarrow \infty\)时，对分母近似，得到
\begin{align}
I(P_\theta)=A^2\,\frac{\sin^2\left(\frac{ka\sin\theta}{2}\right)}{\left( \frac{ka\sin\theta}{2} \right)^2}
=N^2A^2\,\frac{\sin^2(ka\sin\theta /2)}{(ka\sin\theta /2)^2}
=I_0\left( \frac{\sin\alpha}{\alpha} \right) ^2.
\end{align}
与复数积分法的结果一致。\\
比较以上两种方法可以看出，衍射和干涉没有本质区别，都是光波的相干叠加。它们的区别仅仅在于：衍射是连续的次波源发出的无限多束次光波的相干叠加，干涉是分离的有限束几何光线的相干叠加。

\subsubsection{单缝衍射图样的特征}
单缝衍射因子函数\((\sin\alpha /\alpha)^2\)的极值决定了衍射图样的极强和暗纹，在变量\(\alpha=\pi a\sin\theta /\lambda\)中主要考虑\(\theta\)，因为它的取值是可在实验中测量的位置。\\
\textbf{主极强}出现在\(\alpha =0\)即\(\theta =0\)处，即零级衍射斑。\(\theta=0\)保证了各衍射光线之间无光程差，从而它们有相同的相位，能够产生最大的光强。Fermat原理中的实际光线就是零级衍射光线，几何光学中的像点就是零级衍射斑中心。\\
\textbf{次极强}出现在\(\frac{\mathrm d}{\mathrm d\alpha}\left(\frac{\sin\alpha}{\alpha}\right)=0\)处，它们是\(\alpha=\tan\alpha\)的根，数值为
\begin{align*}
\alpha=\pm 1.43\pi,\,\pm 2.46\pi,\,\pm 3.47\pi,\,\cdots
\end{align*}
次极强的光强比主极强小得多，绝大部分能量集中在主极强中。\\
\textbf{暗纹}出现在\(\sin\alpha=0\)且\(\alpha\ne 0\)处，即
\begin{align}
\alpha=m\pi,\quad\sin\theta=m \frac{\lambda}{a}.\quad(m=\pm 1,\,\pm 2,\cdots)
\end{align}
\textbf{半角宽}指从主极强到相邻的第一个暗纹的角间距\(\Delta\theta\)，它用来表征主极强亮纹的宽度。所以零级衍射斑的半角宽为（傍轴近似下）
\begin{align}
\Delta(\sin\theta)&=\cos\theta\Delta\theta=\frac{\lambda}{a},\notag\\
\Delta\theta&=\frac{\lambda}{a\cos\theta}\thickapprox \frac{\lambda}{a}.
\end{align}
可见，对于给定的波长，\(\Delta\theta\)与缝宽成反比，在波前上对光束的约束越强，衍射场越弥散，衍射斑铺张的越宽；反过来，当缝宽很大，光束几乎自由传播时，\(\Delta\theta\rightarrow 0\)，衍射场基本上集中在沿直线传播的方向上，在透镜的后焦面上，衍射斑收缩为几何光学的像点。

\newpage
\subsubsection{例题：Fraunhofer单缝双线衍射}
在焦距\(f\)的正透镜的后焦面上，观察缝宽为\(a\)的Fraunhofer单缝衍射，已知入射光包含两种波长\(\lambda_1,\,\lambda_2\)，\(\lambda_1\)的第\(k_1\)个极小和\(\lambda_2\)的第\(k_2\)个极小出现在距中央主极大\(x\)处的同一点，试由此求出\(\lambda_1,\,\lambda_2\)。\\
\textbf{解}\quad 设\(\lambda_i\)的第\(k_i\)个极小与中央主极大的角距离为\(\theta_i\)，由几何关系
\begin{align*}
x=f\tan\theta_1=f\tan\theta_2,
\end{align*}
根据光强极小
\begin{align*}
\begin{cases}
\sin\theta_1=k_1 \frac{\lambda_1}{a},\\
\sin\theta_2=k_2 \frac{\lambda_2}{a}.
\end{cases}
\end{align*}
为化简结果，采用近似\(\tan\theta\thickapprox \sin\theta\)，此时增加了傍轴条件
\begin{align*}
f\sin\theta_1=f\sin\theta_2.
\end{align*}
于是
\begin{align*}
\begin{cases}
\lambda_1=\frac{ax}{k_1f},\\
\lambda_2=\frac{ax}{k_2f}.
\end{cases}
\end{align*}

\newpage
\subsection{Fraunhofer圆孔衍射}
从衍射装置的轴对称性可以知道，Fraunhofer圆孔衍射图样由一中央亮斑和同心圆环条纹组成。\\
\subsubsection{圆孔衍射光强的计算}
仍用Fresnel-Kirchhoff-Fraunhofer衍射积分公式
\begin{align*}
\tilde E_0(P_\theta)=\frac{-\mathrm i}{\lambda z_0}\iint_{\Sigma_0}E_0(Q)\mathrm e^{\mathrm ikr}\,\mathrm dS.
\end{align*}
设圆孔半径为\(a\)，在圆孔上用极坐标\(\rho,\,\phi\)划分波前，仍设\(\theta\)为衍射光线与主轴的夹角，即衍射角，则由几何关系可知，波前上任一点\(Q\)到场点\(P_\theta\)的光程为
\begin{align*}
r=r_0+\rho\cos\phi\sin\theta,
\end{align*}
其中\(r_0\)是圆孔中心\(O\)到\(P_\theta \)的光程。代入计算得
\begin{align}
\tilde E_0(P_\theta)&=\frac{-\mathrm iE_0(Q)}{\lambda z_0}\iint_{\Sigma_0}\mathrm e^{\mathrm ik(r_0+\rho\cos\phi\sin\theta)}\,\rho\mathrm d\rho\mathrm d\phi
=\frac{-\mathrm iE_0(Q)}{\lambda z_0}\,\mathrm e^{\mathrm ikr_0}\int_0^{2\pi}\mathrm d\phi\int_0^a\mathrm e^{\mathrm ik\rho\cos\phi\sin\theta}\,\rho\mathrm d\rho,\notag\\
&=\frac{-\mathrm i(\pi a^2)E_0(Q)}{\lambda z_0}\,\mathrm e^{\mathrm ikr_0}\left[ \frac{2\mathrm J_1(x)}{x} \right] .
\end{align}
其中\(x=2\pi a\sin\theta /\lambda\)，\(\mathrm J_1(x)\)为一阶Bessel函数。光强分布公式为
\begin{align}
I(P_\theta)=I_0\left[ \frac{2\mathrm J_1(x)}{x} \right] ^2.
\end{align}
容易看出\(I_0\propto (\pi a^2)^2 /(\lambda^2) \)。

\subsubsection{圆孔衍射图样的特征}
\hspace{-2em}\textbf{主极强}在\(\theta=0\)处，即中央亮斑，称作Airy斑，其能量占有全部能量的83.78\%，其中心是几何光学的像点。\\
\textbf{暗环}分布在
\begin{align*}
\sin\theta=0.610 \frac{\lambda}{a},\,1.116 \frac{\lambda}{a},\,1.619 \frac{\lambda}{a},\,\cdots
\end{align*}
两相邻暗环之间有一个次极强，它们是中央亮斑之外的亮环。\\
\textbf{角半径}指Airy斑的大小，即第一暗环的角半径\(\Delta \theta\)，可以衡量衍射光角分布的弥散程度
\begin{align}
\Delta\theta=1.22 \frac{\lambda}{D}.
\end{align}
这就是圆孔衍射的反比关系。\\
\textbf{最小分辨角}\phantom{awd}\\
根据Rayleigh判据：两个Airy斑可以被分辨的极限条件是两个Airy斑的角距离等于每个Airy斑的角半径，最小分辨角\(\updelta\theta\)正是
\begin{align}
\updelta\theta=\Delta\theta=1.22\lambda /D.
\end{align}
它描述了光学仪器分辨点状物体的本领。由上式可知要提高仪器的分辨率，需要增大透镜的直径，或者减小入射光的波长。

\subsubsection{例题：相机的最远分辨距离}
如果相机镜头的焦距为\(f\)，光圈值为\(F\)，所用波长\(\lambda\)，两点间距离\(s\)，试问可以分辨两点的最远距离。\\
\textbf{解}\quad 由光圈值的定义可知相机的直径
\begin{align*}
D=\frac{f}{F}.
\end{align*}
代入最小分辨角即得最远分辨距离，此时依傍轴近似
\begin{align}
L=\frac{s}{\tan(\updelta\theta)}\thickapprox \frac{s}{\updelta\theta}=\frac{sD}{1.22 \lambda}.
\end{align}


\subsection{衍射光栅}
光栅衍射的实质是多束衍射光之间的干涉，因而光栅的衍射场鲜明地表现出“多光束干涉”的基本特征：光栅上被入射光照射的单元越多，衍射条纹就越细锐，这说明叠加后的光场的方向性越强，每条亮纹对应的光束单色性越好。
\subsubsection{Fraunhofer多缝衍射}
设缝宽仍为\(a\)，缝间不透明部分宽度为\(b\)，则相邻狭缝上对应点的距离为\(d=a+b\)称作\textbf{光栅常数}。\par
当平行单色光入射有\(N\)条缝的透射光栅上时，在每条狭缝上都发生衍射，由于各条狭缝宽度相等，每束单缝衍射光在\(P_\theta\)处产生的光振动的振幅都为\(A_0\sin\alpha /\alpha\)。因为各条狭缝位于平行光的同一波面上，所以在该波面上有相同的相位，从而从这\(N\)条缝产生的衍射光都是相干光。又根据透镜的性质，衍射角\(\theta\)相同的平行衍射光都会汇聚到观察屏上相同的\(P_\theta\)点，因此\(P_\theta\)处的总光振动为各束单缝衍射光的多光束干涉。\\
\phantom{awd}\par
相邻两缝的衍射光之间具有相同的光程差和相位差
\begin{align}
\Delta l=d\sin\theta,\quad\delta=2\pi d\sin\theta /\lambda.
\end{align}
代入得到
\begin{align}
\tilde E_0(P_\theta)&=A(\theta)\,\frac{\sin(N\delta /2)}{\sin(\delta /2)}=A_0\,\frac{\sin\alpha}{\alpha}\,\frac{\sin(N\delta /2)}{\sin(\delta /2)},\\
I(P_\theta)&=[A(\theta)]^2\left[ \frac{\sin(N\delta /2)}{\sin(\delta /2)} \right] ^2=A_0^2\left( \frac{\sin\alpha}{\alpha } \right) ^2\left[ \frac{\sin(N\delta /2)}{\sin(\delta /2)} \right] ^2.
\end{align}
这就是多缝衍射的振幅和光强分布公式。

\newpage
\subsubsection{多缝干涉图样的特征}
先分析多缝干涉因子函数\(\left[ \frac{\sin(N\delta /2)}{\sin(\delta /2)} \right] ^2\)，同样关注变量\(\delta=2\pi d\sin\theta /\lambda\)中的\(\theta\)。\\
\textbf{主极强}的位置满足\(\sin(N\delta /2)=0\)且\(\sin(\delta /2)=0\)，即
\begin{align}
d\sin\theta=k\lambda.\quad(k=0,\,\pm 1,\,\pm 2,\,\cdots)
\end{align}
上式称为\textbf{光栅方程}。\\主极强的光强为
\begin{align*}
I_{\max}=N^2A_0^2(\sin\alpha /\alpha)^2,
\end{align*}
可知主极强处光强为单缝衍射光在该方向的光强的\(N^2\)倍，衍射光能量主要集中在主极强条纹中。\\
主极强的数目\(k\)由光栅方程确定，因\(|\sin\theta|\leqslant 1\)，有\(|k|_{\max}=[d /\lambda]\)。\\
\textbf{暗纹}的位置满足\(\sin(N\delta /2)=0\)且\(\sin(\delta /2)\ne 0\)，即
\begin{align}
\sin\theta=\left(k+\frac{m}{N}\right)\frac{\lambda}{d}.\quad(k=0,\,\pm 1,\,\pm 2,\,\cdots;\,m=1,\,\cdots,\,N-1)
\end{align}
可知两个主极强之间有\(N-1\)条暗纹。\\
次极强位于两条相邻的暗纹之间，两个主极强之间有\(N-2\)个次极强。\\
\textbf{半角宽}\phantom{awd}\\
对\(k\)级主极强
\begin{align}
\Delta(\sin\theta_k)=\cos\theta_k\Delta\theta
&=\left( k+\frac{1}{N} \right) \frac{\lambda}{d}-k \,\frac{\lambda}{d}=\frac{\lambda}{Nd},\notag\\
\Delta\theta&=\frac{\lambda}{Nd\cos\theta_k}.
\end{align}
可知主极强的半角宽和\(Nd\)成反比。\\
多缝干涉因子表明，多光束干涉使能量高度集中于各个主极强，并且光栅越长（\(Nd\)越大），方向性越强，主极强条纹越细锐。\\
\phantom{awd}\par
至于单缝衍射因子，其作用有二，一是改变能量在各级主极强之间的分配，使位于单缝衍射亮斑位置的干涉主极强得到更多的能量。\\
其二是产生干涉主极强的\textbf{缺级}现象。满足光栅方程的方向上，本应有相应的干涉主极强出现，但若该方向与单缝衍射的暗纹方向重合，此时合成的光强就为零。因此缺级满足两个方程
\begin{align*}
\sin\theta&=k \,\frac{\lambda}{d},\quad(k=0,\,\pm 1,\,\pm 2,\,\cdots)\\
\sin\theta&=m \,\frac{\lambda}{a}.\quad (m=\pm 1,\,\pm 2,\,\cdots)
\end{align*}
联立得缺级的条件为
\begin{align}
k=\frac{d}{a}\,m.
\end{align}

\newpage
\subsubsection{光栅光谱}
\paragraph{光栅色散}\phantom{awd}\\
若入射光包含不同波长，则每种波长在观察屏上形成各自的衍射图样。由光栅方程可知，对一个光栅（\(d\)一定），除开零级主极强，不同波长的主极强对应不同的衍射角\(\theta_k\)，这就是光栅色散。如果用非单色光照明，可以看到衍射图样中有几套不同颜色的亮线，它们各自对应一个波长。
\paragraph{角色散本领}\phantom{awd}\\
对光栅方程两边取微分可得
\begin{align}
d\cos\theta_k\updelta\theta&=k\updelta\lambda,\notag\\
\mathscr D=\frac{\updelta\theta}{\updelta\lambda}
&=\frac{k}{d\cos\theta_k}.
\end{align}
光栅的角色散本领与光栅常数成反比，为了增强角色散本领，光栅的缝刻得很密；角色散本领还与光谱级数\(k\)成正比，光谱级数越大，角色散本领越强，不同波长的谱线分开的越厉害，但是光强也越小。
\paragraph{色分辨本领}\phantom{awd}\\
根据Rayleigh判据，光栅光谱的最小分辨角是光谱的半角宽度，由\(\Delta\theta=\lambda /(Nd\cos\theta_k)\)，有
\begin{align}
\updelta\lambda=\frac{\updelta\theta}{\mathscr D}
&=\frac{\lambda /(Nd\cos\theta_k)}{k /(d\cos\theta_k)}
=\frac{\lambda}{kN},\notag\\
\mathscr R&=\frac{\lambda}{\updelta\lambda}=kN.
\end{align}

\subsubsection{例题：光栅光谱参数}
\begin{enumerate}
\item 在光栅的\(k\)级光谱中分辨双线\(\lambda_1,\,\lambda_2\)，求光栅缝数\(N\)所需要的最小值；
\item 求在\(\lambda \)附近，光栅的\(k\)级光谱的自由光谱范围。
\end{enumerate}
\textbf{解}\quad 1.由色分辨本领
\begin{align*}
\mathscr R=\frac{\bar \lambda}{\updelta \lambda }=kN
\Rightarrow
N=\frac{\bar \lambda}{k\updelta\lambda}=\frac{\lambda_1+\lambda_2}{2k(\lambda_1-\lambda_2)}.
\end{align*}
\hspace{2em}2.设光栅常数为\(d\)，则
\begin{align*}
\begin{cases}
d\sin\theta=(k+1)\lambda,\\
d\sin\theta=k(\lambda+\Delta\lambda),
\end{cases}
\end{align*}
这就解得了自由光谱范围
\begin{align}
\Delta\lambda=\lambda /k.
\end{align}

先来点背景介绍： 对于二维Hubbard模型， Brinkman&Rice使用的Gutzwiller近似【1】的到了一个金属-绝缘体转变，称为BR transition。这个不同于Mott transition。然后现在用slave-boson试试能不能得到同样的结论和图像。 在之前，Barnes做出了一个成功的Slave-boson 【2】的表示：把电子算符拆成一个费米子和两个玻色子。玻色子分别叫做doublon（用d表示）和holon（用e表示），代表双占据和空穴，费米子带有自旋自由度。这个表示在安德森杂质模型上使用的很好。Coleman 【3】 之后拓展至了一般的格点。但是，为了在Hubbard 模型上和之前的Brinkman&Rice使用的Gutzwiller近似的结果对上，Kotliar 和 Ruckenstein 【4】拓展一个新的表示（KR representation），新引入一个带有自旋自由度的$p$玻色子，表示如下： 

\begin{align} &e^{\dagger}\mathinner{|Vac\rangle} = \mathinner{|0\rangle} \quad non-occuiped \ state \notag \\ &p_{\sigma}^{\dagger}f_{\sigma}^{\dagger}\mathinner{|Vac\rangle} = \mathinner{|\sigma\rangle} \quad singely-occuiped \ state \notag\\ &d^{\dagger}f_{\sigma}^{\dagger}f_{-\sigma}^{\dagger}\mathinner{|Vac\rangle} = \mathinner{|\uparrow\downarrow\rangle} \quad doublely-occuiped \ state \end{align} 

注意这里的|Vac>只是人工的定义。电子算符会拆成如下形式 

\begin{align}c_{i\sigma}=z_{i\sigma}f_{i\sigma},\quad z_{i\sigma} = e^{\dagger}_ip_{i\sigma} + p^{\dagger}_{i\bar\sigma}d_i \end{align}

d，e，p满足玻色对易关系，f满足反对易关系。这并不是一个operator identity，因为还有如下的约束条件（constrains）第一个约束是由每个格点上必须有一类且仅有一类玻色子存在，第二个代表给定spin存在两类等同计算费米子占据数： 

\begin{align} &Q_i =\sum_{\sigma} p^{\dagger}_{i\sigma}p_{i\sigma} + e_i^{\dagger}e_i + d_i^{\dagger}d_i -\mathbf{1} =0 \notag\\ &Q_{i\sigma}=f_{i\sigma}^{\dagger}f_{i\sigma} - p_{i\sigma}^{\dagger}p_{i\sigma} - d_i^{\dagger}d_i =0\qquad for\quad \sigma=\uparrow / \downarrow \label{constrains} \end{align}  我们要计算的体系是二维正方格子上的Hubbard模型，哈密顿量如下： 

\begin{align}\mathcal{H} = \sum_{, \sigma} t_{ij}(c^{\dagger}_{i\sigma}c_{j\sigma}+ h.c.) + U\sum_i\hat{n}_{i\uparrow}\hat{n}_{i\downarrow} \end{align}

第一项是紧束缚hopping，可以带最近邻条件也可以不带，第二项是on-site的库伦势， $\hat{n}_{i\sigma} = c_{i\sigma}^\dagger c_{i\sigma}$为粒子数算符。

我们想得到一个金属-绝缘体转变的相变点并且和使用Gutzwiller平均场的Brinkman&Rice的结果对应上。 现在开始计算： 首先把Hubbard模型用这里新定义的slave-boson重写

\begin{align} \mathcal{H} = \sum_{\sigma}t_{ij}f^{\dagger}_{i\sigma}f_{j\sigma}z^{\dagger}_{i\sigma}z_{j\sigma} + U\sum_id^{\dagger}_id_i \end{align}

在两个约束条件下这个重写是exact的而不是近似的。然后我们把它扔进配分函数的路径积分。我们都知道，对应粒子场 $[\bar\psi, \psi]$，其配分函数可以写成如下路径积分：

\begin{align} \mathcal{Z} = \int\mathcal{D}(\psi, \bar{\psi}) \ e^{-\int_0^{\beta} \rm{d} \tau\cal{L(\tau)}} \\ \mathcal{L}(\tau) = \bar{\psi}\partial_{\tau}\psi+\mathcal{H}(\bar{\psi}, \psi)-\mu N(\bar{\psi}, \psi) \end{align}

我们现在有1，2，3，4四个粒子场，可以直接扔进路径积分~当然，需要带上两个约束条件并乘上拉格朗日乘子 $\cal{L}\rightarrow\cal{L}+\sum_i\lambda_iQ_q + \sum_{i\sigma}\lambda_{i\sigma}Q_{i\sigma}$（回忆一下约束下条件极值问题，我们往下分析是要求 $\cal{L}$ 的极小情形的）。这里的拉格朗日乘子也是动力学场（每个格点都有对应的两个约束关系）！ 

\begin{align} \mathcal{Z} = \int\cal{D}(f_{\sigma}, \bar{f}_{\sigma}) \cal{D}(e, \bar{e}) \cal{D}(d, \bar{d}) \cal{D}(p_{\sigma}, \bar{p}_{\sigma}) \cal{D}\lambda \cal{D}\lambda'_{\sigma} \ e^{- S(\tau)}\end{align}

\begin{align} S(\tau) &= \int_0^\beta \mathrm{d} \tau \sum_i\left[\bar{e}(\partial_{\tau}+\lambda_i)e_i +\sum_{\sigma}\bar{p}_{i\sigma}(\partial_{\tau}+\lambda_i-\lambda'_{i\sigma})p_{i\sigma} +\bar{d}_{i}(\partial_{\tau}+U+\lambda_i-\lambda'_{i\sigma})d_{i}-\lambda_i \right] \\ \notag &+\int_0^\beta \mathrm{d} \tau \sum_{ij\sigma} \bar{f}_{i\sigma}\left( t_{ij}\bar{z}_{i\sigma}z_{j\sigma} + (\partial_{\tau} + \lambda'_{i\sigma} - \mu)\delta_{ij} \right)f_{j\sigma} \label{01} \end{align}

我们写了一个化学势进去，这玩意其实也是拉格朗日乘子。。。我们希望体系是半满的，这是一个约束。 在strong interaction limit下（ $t_{ij}\rightarrow 0$ ）这就是简单的二次型，可以精确算出，结果一致。但我们不关注这个。 

【注意！目前为止看似顺利，但其实有坑！稍后会填掉。这个填坑也是KR representation 在beyond mean-field变得很复杂的问题所在。】 

我们的近似方法依赖于对应的图像——Hubbard U高于某个点时，每个格点上有且仅有一个电子。由于再升高U带来的排斥，电子就呆在自己格点上不动了，自闭了，单粒子移动完全是被抑制的，所以变成了绝缘体（BR转变）。在这个slave boson的图像下就是，只存在单占据，不存在双占据（doublon）和空穴（holon）！ 

所以我们可以直接采取非常聪明的方法做近似——把boson们全都condensate掉就好了~ 把玻色子们的密度当成序参量，当其变成0的时候不就达到半满下全部单占据的情形了嘛！由于半满的情形下，双占据数目（doublon density）和无占据数目（holon density）一定是相等的。所以这里，我们直接写下一个saddle point solution，把d，p，e， $\lambda_i$ , $\lambda'_{i\sigma}$ 都写成uniform的，无dynamics的参数

【所以说这就是一个简单的saddle point分析，用不上Hubbard-Stratonovich变换解耦再取minimum那样做平均场】

粒子密度写成 $\bar d_i d_i = d^2$ 其它同样。 坑来了：在无相互作用极限 $U\rightarrow 0$ 下，这个saddle point会给出 $p^2_{\sigma} = d^2 = e^2 = 1/4$ 这样的均匀的结果（想一想为什么），会造成 $\mathinner{\langle \bar z_{i\sigma}z_{i\sigma}\rangle} = 1/4$ 于是hopping $t_{ij}$ 就变成了原来的1/4。。。整个紧束缚模型多了1/4这个factor。。。这当然是不对的嘛。所以KR做了一个变换：

\begin{align}z_{i\sigma} \rightarrow (1-d^{\dagger}_id_i-p^{\dagger}_{i\sigma}p_{i\sigma})^\alpha z_{i\sigma} (1-e^{\dagger}_ie_i -p^{\dagger}_{i\bar\sigma}p_{i\bar\sigma})^\alpha = L_{i\sigma} z_{i\sigma} R_{j\sigma}，\quad \alpha = -1/2 \end{align}

 这个时候在saddle point下这个1/4就被消除了。L和R在空占据和双占据子空间下是对角的且本征值为1。 我们先令$\mathinner{\langle \bar z_{i\sigma}z_{i\sigma}\rangle} =q_\sigma$ ，它是个关于 $e^2,d^2,p^2_{\sigma}$ 四个参数（已经不是dynamical field了！）的函数。 

在KR saddle 下，对虚时间的求导啥的都可以扔掉了，费米子部分也变成了一个free的部分。接下来就是教科书级的计算了： 我们的路径积分现在只关于费米子f了玻色部分的作用量直接就只是一个函数而不是泛函积分：

\begin{align}S_b = N\beta \left[ \lambda(\sum_{\sigma} p^2_{\sigma} + e^2 + d^2 -1) -\sum_{\sigma}\lambda'_{\sigma} (p^2_{\sigma} + d^2) +Ud^2\right]\end{align}

\begin{align}\mathcal{Z} = e^{-S_b}\int\cal{D}(\bar f_{\sigma},f_{\sigma})\exp\Big(-\int_0^\beta \mathrm{d} \tau \sum_{ij\sigma} \bar{f}_{i\sigma}\left( t_{ij}\bar{z}_{i\sigma}z_{j\sigma} + (\partial_{\tau} + \lambda'_{i\sigma} - \mu)\delta_{ij} \right)f_{j\sigma}\Big) \end{align}

这里不写快速做法，还是写详细一点：时间域和位置域都做傅里叶变换。先是时间域（算熟悉之后就一起做吧，把频率和动量写在一起多舒服） 

$f_{i\sigma}(\tau) = \frac{1}{\sqrt{\beta}}\sum_{\omega_n} f_{i\sigma}(\omega_n)e^{-i\omega_n\tau}$ 使用 $\int_0^\beta e^{-i(\omega_n-\omega_{n'})\tau}=\beta\delta_{nn'}$ 

第一步得到如下作用量： 

\begin{align}S_f[\bar{f},f] = \sum_{ij\sigma}\sum_n \bar{f}_{i\sigma}(\omega_n)[-i\omega_n +（\lambda_{i\sigma}-\mu)\delta_{ij} + t_{ij}q_{\sigma}] f_{j\sigma}(\omega_n) \end{align}

然后对格点坐标做傅里叶变换 （ $t_{ij}$ 是个循环矩阵，所以无所谓hopping近邻不近邻），获得得能带的dispersion $\epsilon_{\vec k}$ 。写到一起： $\xi_{\vec k\sigma}=q_\sigma \epsilon_{\vec k} +\lambda'_\sigma -\mu$ ，作用量完全对角化： 

\begin{align}S_f[\bar{f},f] = \sum_{ij\sigma}\sum_n \bar{f}_{\sigma}(\vec k,\omega_n)[-i\omega_n +\xi_{\vec k\sigma}] f_{\sigma}(\vec k,\omega_n)\end{align}

所以使用grassmann vector的高斯积分，直接得出配分函数，det A 就是对自由度 $\vec k, \omega_n$ 连乘啦。取对数： 

\begin{align}\log\mathcal{Z}= -S_b + \sum_{\sigma} \sum_{\vec k} \sum_n \log(-i\omega_n + \xi_{\vec k\sigma}) \end{align}

松原频率求和可以精确求出。Altland第四章已经帮我们推导过了，直接套公式：

\begin{align}\sum_n \log(-i\omega_n + \xi_{\vec k\sigma}) = \log(1+e^{-\beta\xi_{\vec k\sigma}}) = \log(1+e^{-\beta(q_\sigma \epsilon_\vec k +\lambda'_\sigma -\mu)})\end{align}

下一步就是热力学量啦。在零温的时候，由于 $F = \mathinner{\langle E\rangle}-TS$ ，所以平均能量： 

 \begin{align} \mathinner{\langle E \rangle}/N = -\frac{1}{N}\frac{\partial}{\partial \beta}\log\mathcal{Z}= & \left[ \lambda(\sum_{\sigma} p^2_{\sigma} + e^2 + d^2 -1) -\sum_{\sigma}\lambda'_{\sigma} (p^2_{\sigma} + d^2) +Ud^2\right]\\ &+\frac{1}{N}\sum_{\sigma}\sum_{\vec k}\frac{q_{\sigma}\epsilon_{\vec k}+(\lambda'_{\sigma}-\mu)}{1+e^{\beta(q_{\sigma}\epsilon_{\vec k}+\lambda'_{\sigma}-\mu)}} \end{align} 

 这个式子可以如下简化：1. 只考虑顺磁的情况，这样自旋指标不区分，所以对自旋的求和统一变成乘2。2：particle-hole symmetry，可以得到$ \lambda'_{\sigma} = U/2 = \mu$以及 $\lambda$ 可以任意（这就是拉格朗日乘子的作用，使之满足约束）取 $\lambda = \lambda'_{\sigma}$ 我们可以消掉p-density。现在（不区分自旋指标），在原本的两个约束条件下且满足半满情形下 $d^2=e^2$ ， $\mathinner{\langle \bar z_{i\sigma}z_{i\sigma}\rangle} =q_\sigma = 8d^2(1-2d^2) = q$ 可以只用d-density表示。我们知道doulon和holon的density一定会是相等的。我们把对k的求和化成积分 $\sum_{\mathbf{k}}\rightarrow \frac{N}{(2\pi)^2}\int \rm{d}\mathbf{k}$ ，并插入态密度 $g(E)$ 转到能量的积分： 

\begin{align}\bar{\epsilon} = \mathinner{\langle E \rangle}/N = Ud^2 + 2\int_{-\infty}^{\infty}\mathrm{d} E \ g(E) \frac{qE}{1+e^{\beta qE}} \end{align}

现在，平均能量（自由能）对序参量——doublon （holon）density求极小值：

\begin{align}  \frac{\partial\bar{\epsilon}}{\partial d^2} = \frac{\mathrm{d}q}{\mathrm{d} d^2}\frac{\partial \bar{\epsilon}}{\partial q} = 0 \end{align}

 能得到

 \begin{align} (8-32d^2)\times \left[2\int_{-\infty}^{\infty}\mathrm{d} E\ g(E) E\left( \frac{e^{\beta qE}(1-\beta qE)+1}{(e^{\beta qE}+1)^2}\right) \right] = 0 \end{align}

这一步容易卡住。其实，把中间大圆括号里那一坨扔进画图程序，就能知道这tm就是一个近似的翻转阶梯函数 

\begin{align} f(x) = \frac{e^{x}(1-x)+1}{(e^{x}+1)^2}, \ \lim_{x\rightarrow\infty}f(x) = 0, \ \lim_{x\rightarrow-\infty}f(x) = 1 \end{align}

 而我们正好是要取零温 $\beta \rightarrow +\infty$ ，所以直接把这个式子写成 

\begin{align} d^2 = \frac{1}{4}(1-\frac{U}{U_c}), \quad U_c = 16\int_0^{\infty} \mathrm{d} E g(E) E \end{align}

 在 $U>U_c$ 是，doublon和holon的密度为0，完全变为所有格点单占据。通过代入态密度，数值积分可以轻易得到正方格子下 $U_c \approx 13t$ ，确实是BR转变。 这只是简单的saddle point方法，从正经计算路径积分开始到最后的计算都不难。当然在这套slave boson表示下可以引入其它的平均场，可以得到比如没有玻色condensation但玻色子密度不为零的转变（是Mott转变）。 

参考 

[1] https://journals.aps.org/prb/abstract/10.1103/PhysRevB.2.4302

[2] https://iopscience.iop.org/article/10.1088/0305-4608/7/12/022

[3] https://journals.aps.org/prb/abstract/10.1103/PhysRevB.29.3035

[4] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.57.1362

作者｜yubr
编辑｜Trader Joe's

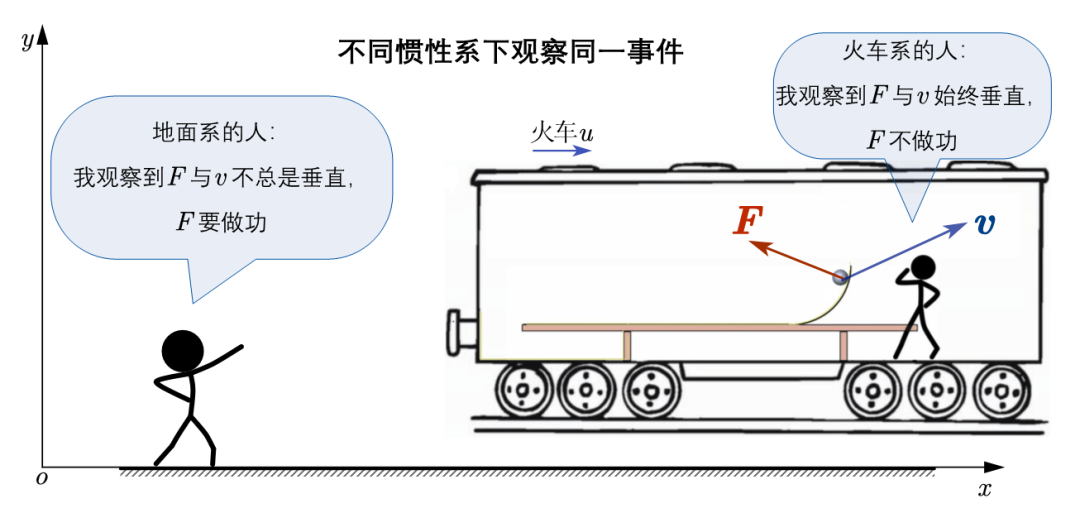
在上一章《四维形式的电磁理论（Ⅰ）》中我们推导了麦克斯韦方程的四维形式，建立了四维语言下电磁理论的基本动力学方程。

本章中，我们将用四维语言描述带电粒子在电磁场中的运动，也就是建立洛伦兹力的四维形式；我们还将显式地给出电磁场在洛伦兹变换下的具体变换规则；最后我们介绍著名的A-B效应（Aharonov–Bohm effect）。

Yakir Aharonov

David Bohm

1. 带电粒子在电磁场中的运动方程——洛伦兹力的四维形式

在我们熟悉的三维矢量语言下，带电粒子在电磁场中的运动由洛伦兹力来决定

$$
\vec{F}_{洛}=\frac{d\vec{p}}{dt}
$$
其中
$$
\vec{F}_{洛}=q\left( \vec{E}+ \frac{\vec{v}}{c}\times \vec{B}\right)
$$

但是显然，这个方程在洛伦兹变换下不是协变的，换言之，在不同的惯性系下观测到的粒子受到的洛伦兹力并不同。

为了更好地描述在不同惯性系下粒子受到的洛伦兹力的关系，我们需要用四维语言改写上面的方程。

在《四维形式的狭义相对论及其动力学》中，我们已经给出了动量和速度的四维形式，所以方程的右边很容易改写：

$$
\frac{d\vec{p}}{dt}\rightarrow \frac{dp^{\mu}}{d\tau}=m\frac{d}{d\tau}U^{\mu}=m\frac{d}{d\tau}(\gamma c,\gamma \vec{v})
$$

我们先来看时间分量：

$$
\begin{aligned}
\frac{d\gamma}{d\tau}&=\gamma\frac{d\gamma}{dt}=\gamma\frac{d}{dt} \left (1- \frac{v^2}{c^2}\right)^{-1/2}\\&=-\frac{1}{2}\gamma\left(1-\frac{v^2}{c^2}\right)^{-3/2}\left(-\frac{2\vec{v}}{c^2}\right)\cdot \frac{d\vec{v}}{dt}\\&=\gamma^4\frac{\vec{v}}{c^2}\cdot\frac{d\vec{v}}{dt}
\end{aligned}
$$
另一方面，
$$
\begin{aligned}
\vec{F}&=\frac{d\vec{p}}{dt}=\frac{d}{dt}\left(\gamma m \vec{v}\right)\\&=m\left(\frac{d\gamma}{dt}\vec{v}+\gamma \frac{d\vec{v}}{dt} \right)\\&=m\left[\frac{\gamma^3}{c^2}\left(\vec{v}\cdot \frac{d\vec{v}}{dt}\right)\vec{v}+\gamma\frac{d\vec{v}}{dt}\right]
\end{aligned}
$$

$$
\begin{aligned}
\vec{F}\cdot \vec{v}&=m\left[ \left(\frac{\gamma^3v^2}{c^2}+\gamma \right)\left(\vec{v}\cdot \frac{d\vec{v}}{dt}\right) \right]\\&=m\gamma^3\left(\vec{v}\cdot \frac{d\vec{v}}{dt}\right)
\end{aligned}
$$

所以
$$
\frac{dp^0}{d\tau}=\frac{\gamma}{c}\vec{F}\cdot\vec{v}
$$

我们再来看空间分量：

$$
\frac{d}{d\tau}\left(\gamma\vec{v}\right)=\gamma\left(\frac{d\gamma}{dt}\vec{v}+\gamma\frac{d\vec{v}}{dt}\right)=\frac{\gamma\vec{F}}{m}
$$
所以
$$
\frac{dp^i}{d\tau}=\gamma\vec{F}
$$
总结一下
$$
\frac{dp^{\mu}}{d\tau}=\left(\frac{\gamma}{c}\vec{F}\cdot\vec{v},\gamma\vec{F}\right)
$$
我们来看看它的物理含义，利用 $p^{\mu}=\left(E/c,\vec{p}\right)$ ，我们有
$$
\begin{aligned}
\frac{d}{d\tau}\left(\frac{E}{c}\right)=\frac{\gamma}{c}\vec{F}\cdot\vec{v}\Rightarrow \frac{dE}{dt}=\vec{F}\cdot\vec{v}
\end{aligned}
$$

这正是能量守恒定律

$$
\frac{d\vec{p}}{d\tau}=\gamma \vec{F}\Rightarrow \frac{d\vec{p}}{dt}=\vec{F}
$$

这正是牛顿第二定律

好，下面我们把三维力以洛伦兹力的具体形式

$$
\vec{F}=q\left( \vec{E}+ \frac{\vec{v}}{c}\times \vec{B}\right)
$$
代入，对时间分量有
$$
\begin{aligned}
\frac{dp^0}{d\tau}&=\frac{\gamma}{c}\vec{F}\cdot\vec{v}\\&=\frac{\gamma}{c}q\left(\vec{E}+\frac{\vec{v}}{c}\times \vec{B}\right)\cdot \vec{v}\\&=\frac{\gamma}{c}q \vec{E}\cdot \vec{v}=\frac{q}{c}\left(\vec{E}\cdot \gamma \vec{v}\right)\\&=\frac{q}{c}E^i U^i=\frac{q}{c}F^{i0}U^{i}\\&=\frac{q}{c}F^{0i}U_i=\frac{q}{c}F^{0\nu}U_{\nu}
\end{aligned}
$$
其中我们用到了电场强度和电磁场张量之间的关系 $E^{i}=F^{i0}$ ，这个关系在上一章 《四维形式的电磁理论（Ⅰ）》（超链接）中已经推导过了。对空间分量我们有
$$
\begin{aligned}
\frac{dp^{i}}{d\tau}&=\gamma F^{i}=\gamma q(\vec{E}+\frac{\vec{v}}{c}\times \vec{B})^{i}\\&=\frac{q}{c}\left(\gamma cE^{i}+\gamma \epsilon_{ijk}v^{j}B^{k} \right)\\&=\frac{q}{c}\left(U^{0}F^{i0}-\frac{1}{2}\epsilon^{ijk}\epsilon^{klm}U^{j}F^{lm}\right)\\&=\frac{q}{c}\left( U^{0}F^{i0} - U^{j}F^{ij}\right)\\&=\frac{q}{c}F^{i\nu}U_{\nu}
\end{aligned}
$$
其中用到了磁场强度和电磁场张量之间的关系 $B^{k}=-\frac{1}{2}\epsilon^{klm}F^{lm}$ 和恒等式 $\epsilon^{ijk}\epsilon^{klm}=\delta^{il}\delta^{jm}-\delta^{im}\delta^{jl} $

合并一下我们就得到了带电粒子在电磁场中的运动方程

$$
\frac{dp^{\mu}}{d\tau}=\frac{q}{c}F^{\mu\nu}U_{\nu}
$$

这是四维形式的运动方程，和三维形式相比最大的优点就是具有显式的洛伦兹协变性。

所以四维形式的洛伦兹力可以定义为

$$
F^{\mu}_{洛}=\frac{q}{c}F^{\mu\nu}U_{\nu}
$$

显然它也是洛伦兹协变的。

2. 电磁场的洛伦兹变换

对于一个电磁场体系，电场 $\vec{E}$ 和磁场 $\vec{B}$ 的描述与电磁场张量 $F^{\mu\nu}$ 的描述完全等价，其对应分量为
$$
F^{\mu\nu}\equiv \left( \begin{array}{cccc} F^{00}&F^{01}&F^{02}&F^{03}\\ F^{10}&F^{11} &F^{12} &F^{13}\\ F^{20}& F^{21}& F^{22}&F^{23}\\F^{30}&F^{31}&F^{32}&F^{33} \end{array} \right) = \left( \begin{array}{cccc} 0&-E^1&-E^2&-E^3\\ E^1&0 &-B^3 &B^2\\ E^2& B^3& 0&-B^1\\E^3&-B^2&B^1&0 \end{array} \right)
$$
采用电磁场张量描述的好处是其具有显式的洛伦兹协变性。

具体地，设 $F^{\mu\nu}$ 和 $F^{\prime\mu\nu}$ 分别为电磁场张量在两个惯性系 $\Sigma$ 和 $\Sigma^{\prime}$ 的分量，两个惯性系之间的洛伦兹变换矩阵为 $\Lambda^{\mu}_{\nu}$ ，则两个惯性系中的分量可以通过如下表达式联系
$$
F^{\prime \mu\nu}=\Lambda^{\mu}_{\rho}\Lambda^{\nu}_{\sigma}F^{\rho\sigma}
$$
或者
$$
F^{\prime}=\Lambda F \Lambda^{T}
$$
下面我们来具体写出电场分量和磁场分量的洛伦兹变换关系。
为简单起见，我们假设两个惯性系的y轴和z轴平行，x轴重合，$\Sigma^{\prime}$ 系相对 $\Sigma$ 系以速度 $v$ 沿x轴正方向平动，则洛伦兹变换矩阵为
$$
\Lambda^{\mu}_{\nu}=\left( \begin{array}{cccc} \gamma&-\gamma \beta&0&0\\ -\gamma\beta&\gamma &0&0\\ 0& 0&1&0\\ 0&0&0&1 \end{array} \right)
$$
其中 $\beta\equiv v/c$ ， $\gamma \equiv 1/\sqrt{1-\beta^2}$ 。从而

*这个公式用图*

最后我们得到
$$
E^{\prime 1}=E^1
$$

$$
E^{\prime 2}=\gamma\left(E^2-\beta B^3\right)
$$

$$
E^{\prime 3}=\gamma\left(E^3+\beta B^2\right)
$$

$$
B^{\prime1}=B^{1}
$$

$$
B^{\prime 2}=\gamma\left(B^2+\beta E^3\right)
$$

$$
B^{\prime 3}=\gamma\left(B^3-\beta E^2\right)
$$

3. Aharonov-Bohm 效应

在上一章 《四维形式的电磁理论（Ⅰ）》（超链接）中我们引入了电磁势 $A^{\mu}=(\phi,\vec{A})$ 来描述电磁场，它和电磁场分量的关系为
$$
\vec{E}=-\nabla\phi-\frac{1}{c}\frac{\partial \vec{A}}{\partial t}
$$

$$
\vec{B}=\nabla \times \vec{A}
$$

一个很自然的问题是，场和势这两种对电磁体系的描述是等价的吗？如果不是，哪一种描述更加基本呢？

首先注意到，在经典电磁体系中，势的描述存在不确定度，即对于一组确定的$(\vec{E},\vec{B})$ 的值，我们可以找到不止一组的 $(\phi,\vec{A})$ 的值与之对应，这称为规范冗余。

具体地说，对原来的标量势和矢量势做如下变换：
$$
\phi\rightarrow\phi^{'}=\phi+\frac{1}{c}\frac{\partial\chi}{\partial t}
$$

$$
\vec{A}\rightarrow \vec{A}^{\prime}=\vec{A}-\nabla \chi
$$

其中 $\chi$ 是一个任意的关于时空坐标的标量函数（不同的 $\chi$ 对应不同的规范），那么对应的电场和磁场并不发生改变
$$
\vec{E}^{\prime}=-\nabla\phi^{\prime}-\frac{1}{c}\frac{\partial \vec{A}^{\prime}}{\partial t}=-\nabla(\phi+\frac{1}{c}\frac{\partial\chi}{\partial t})-\frac{1}{c}\frac{\partial}{\partial t}(\vec{A}-\nabla \chi)=-\nabla\phi-\frac{1}{c}\frac{\partial \vec{A}}{\partial t}=\vec{E}
$$

$$
\vec{B}^{\prime}=\nabla \times \vec{A}^{\prime}=\nabla \times (\vec{A}-\nabla \chi)=\nabla\times \vec{A}=\vec{B}
$$

或者等价地，用四维语言来描述，对于四维势做如下变换：
$$
A^{\mu}\rightarrow A^{\prime \mu}=A^{\mu}+\partial^{\mu}\chi
$$


电磁场张量保持不变
$$
\begin{aligned}
&F^{\mu\nu}\rightarrow F^{\prime \mu\nu}\\=&\partial^{\mu}A^{\nu\prime}-\partial^{\nu}A^{\prime \mu}\\=&\partial^{\mu}\left(A^{\nu}+\partial^{\nu}\chi\right)-\partial^{\nu}\left(A^{\mu}+\partial^{\mu}\chi\right)\\=&\partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu}\\=&F^{\mu\nu}
\end{aligned}
$$

所以，对于经典电磁体系，场的描述比势更加基本。场是物理的，对应可观测量，而势并不是物理的，它不能唯一确定电磁场，不具有可观测效应。

任何可观测量的值都应该不依赖于电磁势对规范的选择（即不依赖于函数$\chi$），这称为规范不变性。

但是，到了量子体系中，这一切都发生了变化。1959年，Aharonov和Bohm指出（Phys. Rev. 115, (1959), 485）：

在量子体系中，电磁势也具有可观测效应。这称为Aharonov-Bohm效应，简称A-B效应。

为此，我们设想如下的实验：

考虑通以稳恒电流 $I$，半径为 $R$，单位长度密绕匝数 $n$ 的无限长通电螺线管，容易计算出，对于这样的电磁体系，螺线管的内部为匀强磁场，方向沿着螺线管的径向，而螺线管外部磁场为零

$$
B(r)=nI,\qquad r < R
$$

$$
B(r)=0,\qquad r > R
$$
通过这个螺线管的磁通量为
$$
\Phi=\int_S \vec{B}\cdot d\vec{S}=n \pi IR^2
$$
但是，螺线管内外的磁矢势都不为零，其方向环绕螺线管的径向
$$
A(r)=\frac{1}{2}nIr ,\qquad r < R
$$

$$
A(r)=\frac{R^2}{2r}nI, \qquad r > R
$$

所以，在螺线管的外部，没有电磁场，但是有电磁势，按照经典电磁理论，螺线管外部不应该有任何可观测效应。

我们现在把这个无限长通电螺线管放入电子的双缝干涉实验中：







我们知道通过双缝的两束电子发生干涉的原因是因为它们到达屏上的时候存在相位差，屏上明暗条纹的具体位置取决于那一点处的相位差。

设螺线管不通电时电子的波函数为 $\psi_{0}$，则由量子力学可以证明，存在矢势时其波函数为
$$
\psi=\psi_0 e^{\frac{ie}{\hbar c}\int_l \vec{A}\cdot d\vec{l} }
$$
在螺线管不通电时，两束电子到达屏上后总的波函数为
$$
\psi_0=\psi^{(1)}_0+\psi^{(2)}_0=|\psi^{(1)}_0|e^{i\phi_1}+|\psi^{(2)}_0|e^{i\phi_2}=\psi^{(1)}_0\left(1+\frac{|\psi_{0}^{(2)}|}{|\psi_{0}^{(1)}|}e^{i(\phi_2-\phi_1)}\right)
$$
其相位差为
$$
\Delta{\phi}_0=\phi_2-\phi_1
$$
而在螺线管通电后， 两束电子到达屏上后总的波函数为
$$
\begin{aligned}
\psi&=\psi^{(1)}+\psi^{(2)}\\&=\psi_{0}^{(1)}e^{\frac{ie}{\hbar c}\int_{l_1} \vec{A}\cdot d\vec{l} }+\psi_{0}^{(2)}e^{\frac{ie}{\hbar c}\int_{l_2} \vec{A}\cdot d\vec{l} }\\&=\psi^{(1)}\left(1+\frac{|\psi_{0}^{(2)}|}{|\psi_{0}^{(1)}|}e^{i\left(\phi_2-\phi_1+\frac{e}{\hbar c}\int_{l_2}\vec{A}\cdot d\vec{l}-\frac{e}{\hbar c}\int_{l_1}\vec{A}\cdot d\vec{l}\right)}\right)
\end{aligned}
$$
其相位差为
$$
\begin{aligned}
\Delta{\phi}&=\phi_2-\phi_1+\frac{e}{\hbar c}\left(\int_{l_2}\vec{A}\cdot d\vec{l}-\int_{l_1}\vec{A}\cdot d\vec{l}\right)\\&=\Delta\phi_0+\frac{e}{\hbar c}\oint_l\vec{A}\cdot d\vec{l}
\end{aligned}
$$


利用Stokes定理，
$$
\oint_l\vec{A}\cdot d\vec{l}=\int_S \vec{B}\cdot d\vec{S}=\Phi_B=n \pi IR^2
$$
所以可以看到螺线管通电前后，相位差改变了
$$
\Delta\phi-\Delta\phi_0=\frac{e}{\hbar c}\Phi_B=\frac{e }{\hbar c}n \pi IR^2
$$
而这会引起屏上明暗条纹的移动，是确确实实的可观测效应。

---

A-B效应告诉我们:

矢势（严格来说应该是矢势的环量，或者磁通量）具有可观测效应。对于量子体系，电磁场的描述并不完全（因为通电前后，螺线管外部的电磁场都为零，但是屏上的条纹却会移动），所以在量子水平上我们应该使用电磁势而不是电磁场来描述电磁体系。

之前提到，矢势具有规范变换下的不确定度，但是可以证明其环量是规范不变的：
$$
\begin{aligned}
\oint_{l} \vec{A}^{\prime}\cdot d\vec{l}&=\oint_{l}\left( \vec{A}-\nabla \chi \right)\cdot d\vec{l}\\&=\oint_{l} \vec{A}\cdot d\vec{l}-\oint_l d\chi\\&=\oint_{l} \vec{A}\cdot d\vec{l}
\end{aligned}
$$


其中利用了梯度积分的性质
$$
\int_a^b \nabla\chi \cdot d\vec{l}=\int_a^b d\chi=\chi(b)-\chi(a)
$$

$$
\oint_{l} \nabla\chi \cdot d\vec{l}=\oint_l d\chi=0
$$

这是合理的，因为矢势的环量具有直接的可观测效应的，理应不依赖于规范的选择。

A-B效应其实对应着非常漂亮的几何图像。按杨振宁先生的观点，20世纪理论物理的三个主旋律分别是：量子化、对称性和相因子。而A-B效应中的A-B相位
$$
\oint_l \vec{A}\cdot d\vec{l}=\int_S \vec{B}\cdot d\vec{S}
$$
是典型的非定域效应。

它告诉我们，定域的电磁场 $(\vec{E},\vec{B})$ 并不能包含电磁体系所有的信息，对于那些不能连续收缩到一点的路径（例如这里的无限长通电螺线管，你在螺线管外面画一个圈包围螺线管，无论怎么收缩都没有办法将这个圈收缩为一个点），仅使用定域的场来描述会丢失体系的一些信息。

而那些丢失的信息就蕴含在了非定域的A-B相位中，它们对应的是这个空间整体的拓扑性质，所有的A-B相位可以按照路径的同伦类进行分类。

1. 三维形式的麦克斯韦方程组

2. 四维流，四维势

3. 规范对称性

4. 电磁场张量

因此， $F^{\mu\nu}$ 是可以直接观测的物理量，并且用它描述电磁场和用 $E$ 和 $B$ 描述电磁场完全等价。

也就是说，$F^{\mu \nu}$ 正是我们要找的 $E$ 和 $B$ 在四维时空的等效物理量，这也是它被称为电磁场张量的原因。

5. 四维形式的麦克斯韦方程组

我们先将上面几节从 $E,B,\rho,J$ 这些三维的电磁学量出发构造得到的四维物理量罗列一下：

四维流 $J^{\mu}\equiv(c\rho,J)$

四维势 $A^{\mu}\equiv(\phi,A)$

其中 $\phi$ 和 $A$ 定义为：$B=\nabla\times A，E=-\nabla \phi-\frac{1}{c}\frac{\partial A}{\partial t} $

电磁场张量 $F^{\mu\nu}\equiv \partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu} $

电磁场对偶张量 $\widetilde{F}^{\mu\nu}\equiv\frac{1}{2}\epsilon^{\mu\nu\alpha\beta}F_{\alpha \beta} $

高斯定理： $\nabla \cdot E=4\pi \rho $

安培环路定理： $\nabla \times B=\frac{4 \pi}{c}J+\frac{1}{c}\frac{\partial E}{\partial t} $

使用四维语言，它们可以等价改写为如下的洛伦兹协变的形式：

$\partial_{\mu}F^{\mu\nu}=\frac{4\pi}{c}J^v \qquad(A) $

注意上式是张量方程，实际上包含了4个分量方程（ $\nu=0,1,2,3$ ），我们来逐个指标地进行验证：

(1) $\nu=0$

方程左边
$$
=\partial_{\mu}F^{\mu 0}=\partial_{0}F^{00}+\partial_{1}F^{10}+\partial_{2}F^{20}+\partial_{3}F^{30}=\partial_1E^1+\partial_2E^2+\partial_3E^3=\nabla\cdot E
$$


方程右边 $=\frac{4\pi}{c}J^0=4\pi\rho$

可以看到这正是高斯定理

(2) $\nu=1$

方程左边
$$
=\partial_{\mu}F^{\mu 1}=\partial_{0}F^{01}+\partial_{1}F^{11}+\partial_{2}F^{21}+\partial_{3}F^{31}=-\frac{1}{c}\partial_t E^1+\partial_2 B^3-\partial_3 B^2
$$
方程右边 $=\frac{4\pi}{c}J^1 $

所以我们得到
$$
\partial_2 B^3-\partial_3 B^2=\frac{4\pi}{c}J^1+\frac{1}{c}\partial_t E^1
$$
也就是
$$
(\nabla \times B)^1=\frac{4\pi}{c}J^1+\frac{1}{c}\frac{\partial E^1}{\partial t}
$$
这正是安培环路定理的第1分量

(3) $\nu=2$

方程左边
$$
=\partial_{\mu}F^{\mu 2}=\partial_{0}F^{02}+\partial_{1}F^{12}+\partial_{2}F^{22}+\partial_{3}F^{32}=-\frac{1}{c}\partial_t E^2-\partial_1 B^3+\partial_3 B^1
$$
方程右边 $=\frac{4\pi}{c}J^2 $

所以我们得到
$$
\partial_3 B^1-\partial_1 B^3=\frac{4\pi}{c}J^2+\frac{1}{c}\partial_t E^2
$$
也就是
$$
(\nabla \times B)^2=\frac{4\pi}{c}J^2+\frac{1}{c}\frac{\partial E^2}{\partial t}
$$
这正是安培环路定理的第2分量

(4) $\nu=3$

和上面完全类似，我们最后得到
$$
\partial_1 B^2-\partial_2 B^1=\frac{4\pi}{c}J^3+\frac{1}{c}\partial_t E^3
$$
也就是
$$
(\nabla \times B)^3=\frac{4\pi}{c}J^3+\frac{1}{c}\frac{\partial E^3}{\partial t}
$$
这正是安培环路定理的第3分量

所以我们看到，$\nu=0$ 的分量方程等价于高斯定理，而 $\nu=1,2,3$ 的分量方程等价于安培环路定理，从而这两个非齐次的麦克斯韦方程确实可以等价改写为方程 $(A)$ 。

接下来我们来看两个齐次的麦克斯韦方程

磁高斯定理： $\nabla \cdot B=0 $

法拉第电磁感应定律：
$$
\nabla \times E=-\frac{1}{c} \frac{\partial B}{\partial t}
$$
它们可以等价改写为：
$$
\partial_{\mu}\widetilde{F}^{\mu\nu}=0 \qquad(B)
$$
我们同样逐个指标进行验证

$\nu=0$
$$
\partial_{\mu} \widetilde{F}^{\mu0}=\partial_{0} \widetilde{F}^{00}+\partial_{1} \widetilde{F}^{10}+\partial_{2} \widetilde{F}^{20}+\partial_{3} \widetilde{F}^{30}=\partial_1 B^1+ \partial_2 B^2+\partial_3 B^3=\nabla \cdot B=0
$$
这正是磁高斯定理

$\nu=1,2,3$
$$
\partial_{\mu} \widetilde{F}^{\mu1}=\partial_{0} \widetilde{F}^{01}+\partial_{1} \widetilde{F}^{11}+\partial_{2} \widetilde{F}^{21}+\partial_{3} \widetilde{F}^{31}=-\frac{1}{c}\partial_t B^1-\partial_2 E^3+\partial_3 E^2=-\frac{1}{c}\partial_t B^1-(\nabla \times B)^1=0
$$

$$
\partial_{\mu} \widetilde{F}^{\mu2}=\partial_{0} \widetilde{F}^{02}+\partial_{1} \widetilde{F}^{12}+\partial_{2} \widetilde{F}^{22}+\partial_{3} \widetilde{F}^{32}=-\frac{1}{c}\partial_t B^2+\partial_1 E^3-\partial_3 E^1=-\frac{1}{c}\partial_t B^2-(\nabla \times B)^2=0
$$

$$
\partial_{\mu} \widetilde{F}^{\mu3}=\partial_{0} \widetilde{F}^{03}+\partial_{1} \widetilde{F}^{13}+\partial_{2} \widetilde{F}^{23}+\partial_{3} \widetilde{F}^{33}=-\frac{1}{c}\partial_t B^3-\partial_1 E^2+\partial_2 E^1=-\frac{1}{c}\partial_t B^3-(\nabla \times B)^3=0
$$

它们正是法拉第电磁感应定律

所以，这两个齐次的麦克斯韦方程确实可以等价改写为方程 $(B)$ $^3$。

总结一下，原本三维空间的四个麦克斯韦方程，在使用四维语言后，可以等效地用两个张量方程来替换
$$
\begin{aligned}
\partial_{\mu}F^{\mu\nu}=\frac{4\pi}{c}J^v \qquad(A)\\
\partial_{\mu}\widetilde{F}^{\mu\nu}=0 \qquad(B)
\end{aligned}
$$
相比之前三维形式的四个矢量方程，这两个张量方程显得简洁了很多。

Footnote

1. 不同惯性系的四维体积元之间差一个洛伦兹变换矩阵的雅可比行列式的绝对值，而从洛伦兹群的定义出发，我们知道它等于1，所以在不同惯性系下的四维体积元都相等。注意，这并不平凡！时空坐标在不同的惯性系中的值都可以不等：$(ct,x,y,z)\neq(ct^{\prime},x^{\prime},y^{\prime},z^{\prime}) $，它们三维体积元也可以不等：$dxdydz\neq dx^{\prime}dy^{\prime}dz^{\prime} $，但是它们的四维体积元必然相等：$cdtdxdydz=cdt^{\prime} dx^{\prime}dy^{\prime}dz^{\prime} $。这正是使用四维语言的好处：因为我们的时空就是四维的，所有普遍来讲，四维的量比三维的量更具有在时空变换（即洛伦兹变换）下的不变性。
2. 例如，如果我们在某个惯性系中观察发现只有电场没有磁场，那么$F^{\mu\nu}F_{\mu\nu}=-2(E^2-B^2)=-2E^2<0$，但是我们知道$F^{\mu\nu}F_{\mu\nu}$是不变量，从而在任何惯性系中它的值都不变，所以我们至少可以得出如下结论：不可能存在某个惯性系，使得在这个惯性系中观察只有磁场没有电场。因为如若不然，在那个参考系中计算出的$F^{\mu\nu}F_{\mu\nu}$的值将大于0，这和它是不变量矛盾。
3. 这里需要指出的是，描述电磁场的动力学的实际上只有方程 (A) ，而方程 (B) 实际上只是数学上的恒等式，被称为Bianchi恒等式，下面我们来证明它：

4. $$
   \widetilde{F}^{\mu\nu}=\frac{1}{2}\epsilon^{\mu\nu\rho\sigma}F_{\rho\sigma}=\frac{1}{2}\epsilon^{\mu\nu\rho\sigma}(\partial_{\rho}A_{\sigma}-\partial_{\sigma}A_{\rho})=\epsilon^{\mu\nu\rho\sigma}\partial_{\rho}A_{\sigma}
   $$
   
   从而
   $$
   \partial_{\mu}\widetilde F^{\mu\nu}=\epsilon^{\mu\nu\rho\sigma}\partial_{\mu}\partial_{\rho}A_{\sigma}=\epsilon^{\rho\nu\mu\sigma}\partial_{\rho}\partial_{\mu}A_{\sigma}=-\epsilon^{\mu\nu\rho\sigma}\partial_{\mu}\partial_{\rho}A_{\sigma}=-\partial_{\mu}\widetilde F^{\mu\nu}
   $$
   所以
   $$
   \partial_{\mu}\widetilde F^{\mu\nu}\equiv0
   $$

5. 一个非常自然的疑问是，既然方程 (B) 只是一个数学上的恒等式，那么它为什么还能描述两个麦克斯韦方程呢？这个问题的答案是，在使用了势 $(\phi,A)$ 的形式而非场 $(E,B)$ 的形式描述电磁场后，方程 (B) 所对应的磁高斯定理和法拉第电磁感应定律就自动成立了

   $$
   \nabla\cdot B=\nabla\cdot(\nabla \times A)=0
   $$
   
   $$
   \nabla \times E=\nabla \times (-\nabla \phi-\frac{1}{c}\frac{\partial A}{\partial t})=-\frac{1}{c}\frac{\partial}{\partial t}(\nabla\times A)=-\frac{1}{c}\frac{\partial B}{\partial t}
   $$

   换句话说，我们可以按照上述方式去定义标量势和矢量势，实际上已经默认使用了磁高斯定理和法拉第电磁感应定律了。

作者｜胡竭末