四维形式的电磁理论(Ⅰ)
编辑|Trader Joe's
1. 三维形式的麦克斯韦方程组
在我们熟悉的三维语言中,描述电磁场的物理量是电场强度 $E$ 和磁感应强度 $B$ ,描述它们随时空分布的动力学方程是麦克斯韦方程组(高斯制,不考虑介质):
$$
\nabla \cdot E=4\pi \rho
$$
$$
\nabla \cdot B=0
$$
$$
\nabla \times E=-\frac{1}{c} \frac{\partial B}{\partial t}
$$
$$
\nabla \times B=\frac{4 \pi}{c}J+\frac{1}{c}\frac{\partial E}{\partial t}
$$
其中 $\rho$ 和 $J$分别是电荷密度和电流密度。将第四式两边取散度并将第一式代入,我们就能得到连续性方程:
$$
\nabla\cdot J+\frac{\partial \rho}{\partial t}=0
$$

2. 四维流,四维势

$$
J^{\mu}\equiv(c\rho,J)
$$
下面我们来证明,这样定义的 $J^{\mu}$ 确实是一个四矢量。
$$
d^3x\equiv dxdydz\equiv dx^1dx^2dx^3
$$
是三维体积元。
$$
d^4x\equiv cdt dxdydz\equiv dx^0d^3x
$$
也是标量$^1$。对电荷的微分形式两边乘上 $dx^0$ ,得到 $dqdx^0=\rho d^4x$ 。
因为 $dq$ 和 $d^4x$ 均为标量,所以 $\rho$ 的变换性质必然和 $dx^0$ 相同。
再考虑再 $dt$ 时间内通过面元 $dx^2dx^3$ 的电荷量: $dq=J\cdot dSdt=J^1dx^2dx^3dx^0/c$ 所以 $cdqdx^1=J^1 d^4x$。因为 $dq$ 和$d^4x$ 均为标量,所以 $J^1$ 的变换性质必然和 $cdx^1$ 相同。同理, $J^i(i=2,3) $ 的变换性质和 $ cdx^i $相同。
所以 $J^{\mu}=(c\rho,J^1,J^2,J^3)$ 的变换性质和 $dx^{\mu}=(dx^0,dx^1,dx^2,dx^3)$ 相同,而后者我们已经证明过是一个四矢量,所以 $J^{\mu}$ 也是一个四矢量。证毕。
$$
\partial_{\mu}J^{\mu}=0
$$
第二步,我们想使用三维的电场强度 $E$ 和磁感应强度 $B$ 来构造新的四维量。首先我们定义如下的标量势 $\phi$ 和矢量势 $A$ :
$$
B=\nabla \times A
$$
$$
E=-\nabla\phi-\frac{1}{c}\frac{\partial A}{\partial t}
$$
然后将 $\phi$ 和 $A$ 放到一起,构成四维势: $A^{\mu}\equiv(\phi,A)$ 。这里需要注意的是,$\phi$ 和 $A$ 构成一个四矢量只是一个假定,它的正确性由其推出的可由实验验证的结论的正确性保证。
3. 规范对称性

$$
\phi\rightarrow\phi^{'}=\phi+\frac{1}{c}\frac{\partial\chi}{\partial t}
$$
$$
A\rightarrow A^{\prime}=A-\nabla \chi
$$
其中 是一个任意的关于时空坐标的标量函数,那么对应的电场和磁场并不发生改变:
$$
B^{\prime}=\nabla \times A^{\prime}=\nabla \times (A-\nabla \chi)=\nabla\times A=B
$$
$$
E^{\prime}=-\nabla\phi^{\prime}-\frac{1}{c}\frac{\partial A^{\prime}}{\partial t}=-\nabla(\phi+\frac{1}{c}\frac{\partial\chi}{\partial t})-\frac{1}{c}\frac{\partial}{\partial t}(A-\nabla \chi)=-\nabla\phi-\frac{1}{c}\frac{\partial A}{\partial t}=E
$$
但是我们知道通过 $E$ 和 $B$ 已经可以充分地描述电磁理论了,也就是说,可观测的物理量只有 $E$ 和 $B$ ,既然上述对于势的变换不改变 $E$ 和 $B$,那么这种变换就是非物理的,这意味着我们可以任意选择标量函数 $\chi$ 的形式,而不改变物理实质。
$$
A^{\mu}\rightarrow A^{\prime \mu}=A^{\mu}+\partial^{\mu}\chi
$$
注意这里我们采用了如下记号:
$$
\partial_{\mu}\equiv\frac{\partial}{\partial x^{\mu}}=(\frac{1}{c}\frac{\partial}{\partial t},\nabla)
$$
$$
\partial^{\mu}\equiv\eta^{\mu\nu}\partial_{\nu}=\frac{\partial}{\partial x_{\mu}}=(\frac{1}{c}\frac{\partial}{\partial t},-\nabla)
$$
4. 电磁场张量

$$
F^{\mu\nu}\equiv\partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu}
$$
首先从定义可以看出, $F^{\mu \nu}$ 是个二阶反对称张量: $F^{\mu \nu}=-F^{\nu \mu}$ ,将具体的指标代入,我们很容易得到它的分量形式
$$
F^{0i}=-E^i, i=1,2,3
$$
$$
F^{12}=-B^3, F^{31}=-B^2, F^{23}=-B^1
$$
写成矩阵形式更加一目了然
$$
\begin{aligned}
F^{\mu\nu}&\equiv \left( \begin{array}{cccc} F^{00}&F^{01}&F^{02}&F^{03}\\ F^{10}&F^{11} &F^{12} &F^{13}\\ F^{20}& F^{21}& F^{22}&F^{23}\\F^{30}&F^{31}&F^{32}&F^{33} \end{array} \right)
\\&= \left( \begin{array}{cccc} 0&-E^1&-E^2&-E^3\\ E^1&0 &-B^3 &B^2\\ E^2& B^3& 0&-B^1\\E^3&-B^2&B^1&0 \end{array} \right)
\end{aligned}
$$
我们可以看到,$F^{\mu \nu}$ 的分量包含了所有电场和磁场的分量,作为四维的二阶反对称张量,$F^{\mu \nu}$ 具有 $C^2_4=6$ 个独立的分量,正好分别对应电场强度的三个分量和磁感应强度的三个分量。
因此, $F^{\mu\nu}$ 是可以直接观测的物理量,并且用它描述电磁场和用 $E$ 和 $B$ 描述电磁场完全等价。
也就是说,$F^{\mu \nu}$ 正是我们要找的 $E$ 和 $B$ 在四维时空的等效物理量,这也是它被称为电磁场张量的原因。
$$
\widetilde{F}^{\mu\nu}\equiv\frac{1}{2}\epsilon^{\mu\nu\alpha\beta}F_{\alpha \beta}=\frac{1}{2}\epsilon^{\mu\nu\alpha\beta}\eta_{\alpha\rho}\eta_{\beta\sigma}F^{\rho\sigma}
$$
其中 $\epsilon^{\mu\nu\alpha\beta}$ 是四阶全反对称张量,并且约定 $\epsilon^{0123}=1$ 。将 $F^{\mu \nu}$ 的分量代入,我们很容易得到 $\widetilde{F}^{\mu\nu}$ 的分量形式
$$
\begin{aligned}
\widetilde{F}^{\mu\nu}&\equiv \left( \begin{array}{cccc} \widetilde{F}^{00}&\widetilde{F}^{01}&\widetilde{F}^{02}&\widetilde{F}^{03}\\ \widetilde{F}^{10}&\widetilde{F}^{11} &\widetilde{F}^{12} &\widetilde{F}^{13}\\ \widetilde{F}^{20}& \widetilde{F}^{21}& \widetilde{F}^{22}&\widetilde{F}^{23}\\\widetilde{F}^{30}&\widetilde{F}^{31}&\widetilde{F}^{32}&\widetilde{F}^{33} \end{array} \right)
\\&= \left( \begin{array}{cccc} 0&-B^1&-B^2&-B^3\\ B^1&0 &E^3 &-E^2\\ B^2& -E^3& 0&E^1\\B^3&E^2&-E^1&0 \end{array} \right)
\end{aligned}
$$
利用 $F^{\mu\nu}$ 和 $\widetilde{F}^{\mu\nu}$ ,我们可以构造出两个重要的洛伦兹不变量(请大家自己代入验证):
1. $F^{\mu\nu}F_{\mu\nu}=-\widetilde{F}^{\mu\nu}\widetilde{F}_{\mu\nu}=-2(E^2-B^2) $
2. $\widetilde{F}^{\mu\nu}F_{\mu\nu}=-4E\cdot B$
接下来,我们将使用电磁场张量 $F^{\mu\nu}$ 和电磁场对偶张量 $\widetilde{F}^{\mu\nu}$ 来将麦克斯韦方程组等价改写为洛伦兹协变的形式。
5. 四维形式的麦克斯韦方程组
我们先将上面几节从 $E,B,\rho,J$ 这些三维的电磁学量出发构造得到的四维物理量罗列一下:
四维流 $J^{\mu}\equiv(c\rho,J)$
四维势 $A^{\mu}\equiv(\phi,A)$
其中 $\phi$ 和 $A$ 定义为:$B=\nabla\times A,E=-\nabla \phi-\frac{1}{c}\frac{\partial A}{\partial t} $
电磁场张量 $F^{\mu\nu}\equiv \partial^{\mu}A^{\nu}-\partial^{\nu}A^{\mu} $
电磁场对偶张量 $\widetilde{F}^{\mu\nu}\equiv\frac{1}{2}\epsilon^{\mu\nu\alpha\beta}F_{\alpha \beta} $
高斯定理: $\nabla \cdot E=4\pi \rho $
安培环路定理: $\nabla \times B=\frac{4 \pi}{c}J+\frac{1}{c}\frac{\partial E}{\partial t} $
使用四维语言,它们可以等价改写为如下的洛伦兹协变的形式:
$\partial_{\mu}F^{\mu\nu}=\frac{4\pi}{c}J^v \qquad(A) $
注意上式是张量方程,实际上包含了4个分量方程( $\nu=0,1,2,3$ ),我们来逐个指标地进行验证:
(1) $\nu=0$
方程左边
$$
=\partial_{\mu}F^{\mu 0}=\partial_{0}F^{00}+\partial_{1}F^{10}+\partial_{2}F^{20}+\partial_{3}F^{30}=\partial_1E^1+\partial_2E^2+\partial_3E^3=\nabla\cdot E
$$
方程右边 $=\frac{4\pi}{c}J^0=4\pi\rho$
可以看到这正是高斯定理
(2) $\nu=1$
方程左边
$$
=\partial_{\mu}F^{\mu 1}=\partial_{0}F^{01}+\partial_{1}F^{11}+\partial_{2}F^{21}+\partial_{3}F^{31}=-\frac{1}{c}\partial_t E^1+\partial_2 B^3-\partial_3 B^2
$$
方程右边 $=\frac{4\pi}{c}J^1 $
所以我们得到
$$
\partial_2 B^3-\partial_3 B^2=\frac{4\pi}{c}J^1+\frac{1}{c}\partial_t E^1
$$
也就是
$$
(\nabla \times B)^1=\frac{4\pi}{c}J^1+\frac{1}{c}\frac{\partial E^1}{\partial t}
$$
这正是安培环路定理的第1分量
(3) $\nu=2$
方程左边
$$
=\partial_{\mu}F^{\mu 2}=\partial_{0}F^{02}+\partial_{1}F^{12}+\partial_{2}F^{22}+\partial_{3}F^{32}=-\frac{1}{c}\partial_t E^2-\partial_1 B^3+\partial_3 B^1
$$
方程右边 $=\frac{4\pi}{c}J^2 $
所以我们得到
$$
\partial_3 B^1-\partial_1 B^3=\frac{4\pi}{c}J^2+\frac{1}{c}\partial_t E^2
$$
也就是
$$
(\nabla \times B)^2=\frac{4\pi}{c}J^2+\frac{1}{c}\frac{\partial E^2}{\partial t}
$$
这正是安培环路定理的第2分量
(4) $\nu=3$
和上面完全类似,我们最后得到
$$
\partial_1 B^2-\partial_2 B^1=\frac{4\pi}{c}J^3+\frac{1}{c}\partial_t E^3
$$
也就是
$$
(\nabla \times B)^3=\frac{4\pi}{c}J^3+\frac{1}{c}\frac{\partial E^3}{\partial t}
$$
这正是安培环路定理的第3分量
所以我们看到,$\nu=0$ 的分量方程等价于高斯定理,而 $\nu=1,2,3$ 的分量方程等价于安培环路定理,从而这两个非齐次的麦克斯韦方程确实可以等价改写为方程 $(A)$ 。
接下来我们来看两个齐次的麦克斯韦方程
磁高斯定理: $\nabla \cdot B=0 $
法拉第电磁感应定律:
$$
\nabla \times E=-\frac{1}{c} \frac{\partial B}{\partial t}
$$
它们可以等价改写为:
$$
\partial_{\mu}\widetilde{F}^{\mu\nu}=0 \qquad(B)
$$
我们同样逐个指标进行验证
$\nu=0$
$$
\partial_{\mu} \widetilde{F}^{\mu0}=\partial_{0} \widetilde{F}^{00}+\partial_{1} \widetilde{F}^{10}+\partial_{2} \widetilde{F}^{20}+\partial_{3} \widetilde{F}^{30}=\partial_1 B^1+ \partial_2 B^2+\partial_3 B^3=\nabla \cdot B=0
$$
这正是磁高斯定理
$\nu=1,2,3$
$$
\partial_{\mu} \widetilde{F}^{\mu1}=\partial_{0} \widetilde{F}^{01}+\partial_{1} \widetilde{F}^{11}+\partial_{2} \widetilde{F}^{21}+\partial_{3} \widetilde{F}^{31}=-\frac{1}{c}\partial_t B^1-\partial_2 E^3+\partial_3 E^2=-\frac{1}{c}\partial_t B^1-(\nabla \times B)^1=0
$$
$$
\partial_{\mu} \widetilde{F}^{\mu2}=\partial_{0} \widetilde{F}^{02}+\partial_{1} \widetilde{F}^{12}+\partial_{2} \widetilde{F}^{22}+\partial_{3} \widetilde{F}^{32}=-\frac{1}{c}\partial_t B^2+\partial_1 E^3-\partial_3 E^1=-\frac{1}{c}\partial_t B^2-(\nabla \times B)^2=0
$$
$$
\partial_{\mu} \widetilde{F}^{\mu3}=\partial_{0} \widetilde{F}^{03}+\partial_{1} \widetilde{F}^{13}+\partial_{2} \widetilde{F}^{23}+\partial_{3} \widetilde{F}^{33}=-\frac{1}{c}\partial_t B^3-\partial_1 E^2+\partial_2 E^1=-\frac{1}{c}\partial_t B^3-(\nabla \times B)^3=0
$$
它们正是法拉第电磁感应定律
所以,这两个齐次的麦克斯韦方程确实可以等价改写为方程 $(B)$ $^3$。
总结一下,原本三维空间的四个麦克斯韦方程,在使用四维语言后,可以等效地用两个张量方程来替换
$$
\begin{aligned}
\partial_{\mu}F^{\mu\nu}=\frac{4\pi}{c}J^v \qquad(A)\\
\partial_{\mu}\widetilde{F}^{\mu\nu}=0 \qquad(B)
\end{aligned}
$$
相比之前三维形式的四个矢量方程,这两个张量方程显得简洁了很多。
Footnote
不同惯性系的四维体积元之间差一个洛伦兹变换矩阵的雅可比行列式的绝对值,而从洛伦兹群的定义出发,我们知道它等于1,所以在不同惯性系下的四维体积元都相等。注意,这并不平凡!时空坐标在不同的惯性系中的值都可以不等:$(ct,x,y,z)\neq(ct^{\prime},x^{\prime},y^{\prime},z^{\prime}) $,它们三维体积元也可以不等:$dxdydz\neq dx^{\prime}dy^{\prime}dz^{\prime} $,但是它们的四维体积元必然相等:$cdtdxdydz=cdt^{\prime} dx^{\prime}dy^{\prime}dz^{\prime} $。这正是使用四维语言的好处:因为我们的时空就是四维的,所有普遍来讲,四维的量比三维的量更具有在时空变换(即洛伦兹变换)下的不变性。 例如,如果我们在某个惯性系中观察发现只有电场没有磁场,那么$F^{\mu\nu}F_{\mu\nu}=-2(E^2-B^2)=-2E^2<0$,但是我们知道$F^{\mu\nu}F_{\mu\nu}$是不变量,从而在任何惯性系中它的值都不变,所以我们至少可以得出如下结论:不可能存在某个惯性系,使得在这个惯性系中观察只有磁场没有电场。因为如若不然,在那个参考系中计算出的$F^{\mu\nu}F_{\mu\nu}$的值将大于0,这和它是不变量矛盾。 这里需要指出的是,描述电磁场的动力学的实际上只有方程 (A) ,而方程 (B) 实际上只是数学上的恒等式,被称为Bianchi恒等式,下面我们来证明它: $$
\widetilde{F}^{\mu\nu}=\frac{1}{2}\epsilon^{\mu\nu\rho\sigma}F_{\rho\sigma}=\frac{1}{2}\epsilon^{\mu\nu\rho\sigma}(\partial_{\rho}A_{\sigma}-\partial_{\sigma}A_{\rho})=\epsilon^{\mu\nu\rho\sigma}\partial_{\rho}A_{\sigma}
$$
从而
$$
\partial_{\mu}\widetilde F^{\mu\nu}=\epsilon^{\mu\nu\rho\sigma}\partial_{\mu}\partial_{\rho}A_{\sigma}=\epsilon^{\rho\nu\mu\sigma}\partial_{\rho}\partial_{\mu}A_{\sigma}=-\epsilon^{\mu\nu\rho\sigma}\partial_{\mu}\partial_{\rho}A_{\sigma}=-\partial_{\mu}\widetilde F^{\mu\nu}
$$
所以
$$
\partial_{\mu}\widetilde F^{\mu\nu}\equiv0
$$一个非常自然的疑问是,既然方程 (B) 只是一个数学上的恒等式,那么它为什么还能描述两个麦克斯韦方程呢?这个问题的答案是,在使用了势 $(\phi,A)$ 的形式而非场 $(E,B)$ 的形式描述电磁场后,方程 (B) 所对应的磁高斯定理和法拉第电磁感应定律就自动成立了 $$
换句话说,我们可以按照上述方式去定义标量势和矢量势,实际上已经默认使用了磁高斯定理和法拉第电磁感应定律了。
\nabla\cdot B=\nabla\cdot(\nabla \times A)=0
$$
$$
\nabla \times E=\nabla \times (-\nabla \phi-\frac{1}{c}\frac{\partial A}{\partial t})=-\frac{1}{c}\frac{\partial}{\partial t}(\nabla\times A)=-\frac{1}{c}\frac{\partial B}{\partial t}
$$
收起阅读 »
相空间语言下的哈密顿力学简介
自牛顿建立力学以来,经典力学已经有了充分系统的发展。其中最主流的三种力学体系分别为牛顿力学,拉格朗日力学和哈密顿力学(后两者通常合称为分析力学)。
可以证明这三种力学体系是等价的,他们都描述了经典力学并给后来的物理发展带来了巨大的贡献。

本文的主要目的是简单介绍数学语言是如何描述哈密顿力学的,为了避免文章过于冗长,本文只会考虑完整约束系统的哈密顿力学,并且哈密顿量总是不显含时间的。
一、分析力学回顾
一个质点系统,如果最多只需要 n 个独立的坐标便可确定它的位置,那么我们把 n 称为它的自由度,把这 n 个坐标称为广义坐标,这n个广义坐标构成的空间称为位形空间。
注意,这里的 n 个坐标并不一定是笛卡尔坐标,它的选取相当任意,只要可以用来描述这个质点系统的位置便可。
仅仅只有这 n 个广义坐标还不足以确定系统的动力学演化,我们还需要知道此时的广义速度,有了这些,我们可以定义一个被称为拉格朗日量的东西,这是个关于广义坐标和广义速度的函数
假设时刻 和 系统位置为 和 ,那么对拉格朗日量以参数 进行积分,得到一个作用量 ,如下
根据最小作用量原理,真实的运动是作用量 取极小值时的情况,因此对 做变分,可以得到著名的欧拉-拉格朗日方程(简称欧拉方程)
理论上只需要解上述方程就可以得到运动方程。

(欧拉 图)

(拉格朗日 图)
二阶方程通常不好解,因此我们可以通过一种被称为勒让德变换的手段,将这个二阶方程转换成两个一阶方程。接下来讲解这是怎么做到的。
利用勒让德变换定义一个新的量
我们把这新的变量称为广义动量,然后定义一个新的函数
这个新函数称为哈密顿量。
注意,此时我们已经通过勒让德变换把变量 转变成了,因此,哈密顿函数定义里的 应该理解为 和 的函数,所以哈密顿量是一个广义坐标和广义动量的函数。
此时你可以使用最小作用量原理,从而得到两个一阶微分方程
这就是大名鼎鼎的哈密顿正则方程。
在结束本小节前我想强调,尽管以上过程似乎是用拉格朗日力学“推出”哈密顿力学,但这只是为了方便理论的引出和阐述。
事实上我们可以分别直接使用欧拉方程或者正则方程作为理论的起点,从而这两个理论完完全全是独立等价的。对于分析力学的更多内容读者可以翻阅[1][2](见文末)
二、流形的引入
为了在数学上严格描述,我们需要借助流形的概念。如前所述,仅有位置是不足以描述运动情况的,因此我们需要一个比位形空间“更大”的空间。

考察后发现,这个空间正是位形空间的切丛 。
因此,拉格朗日量实际是定义在位形空间切丛上的一个函数
那么我们通过勒让德变换改变了其中的变量 为 是否说明这是在切丛上换了一组坐标呢?
答案是——否!观察勒让德变换
我们发现 是逆变,而 却是协变的!
因此勒让德变换实际是一个从切丛到余切丛的映射
而哈密顿量则是一个定义在余切丛上的函数
位形空间的余切丛在物理上通常也称为相空间,由于我们接下来只会处理哈密顿力学,因此之后都称其为相空间。
三、相空间上的哈密顿力学
在介绍相空间上的哈密顿力学前,我们首先定义一个比较抽象的结构。
设在偶数维流形 上给定一个2-形式 ,如果这个 满足以下两个条件
是非退化的
那么我们就给定了流形一个辛形式,这样的流形称为辛流形。
辛形式的定义是比较抽象甚至怪异的,我相信第一次看到这个东西的人普遍不知道这样的结构的意义是什么。
不过没有关系,我们并不打算在这讲解这个结构会带来如何丰富的数学内容(事实上,辛几何早已脱离了物理,成为一个独立的蓬勃发展的基础数学研究领域),而只是来看看利用这样的形式能帮助我们怎样描述哈密顿力学。
让我们回到相空间上,由于相空间是位形空间的余切丛,因此它自然是偶数维的,然后我们定义一个2-形式,如下所示
例如对于一个二维相空间,,对于四维相空间
以此类推。
很容易可以验证,这样定义的2-形式满足辛形式的定义,因此我们就给出了相空间上的一个辛结构。
辛形式是个2-形式,因此我们可以借助它建立一个矢量空间到对偶矢量空间的映射
而哈密顿量是相空间的函数,因此我们可以对它进行一次外微分,如果我们要求某个矢量场在辛形式的映射下正好等于哈密顿量外微分后的对偶矢量,即
我们称这样的矢量场 为哈密顿矢量场,由微分方程的解的唯一性定理可知,一个矢量场总可以给出一条积分曲线,哈密顿矢量场给出的积分曲线正是物理状态在相空间中的演化轨迹!
由于这个结果很重要,我们将在这给出证明。
证:
代入 中,得
对比两边可知,分量正是我们的哈密顿正则方程 Q.E.D.
一个物理量 F 会如何得随物理态的演化而变化,这在相空间上就是,随着演化轨迹物理量如何变化。
我们已经知道了演化轨迹生成的矢量场是哈密顿矢量场,因此,一个物理量的变化正是在哈密顿矢量场方向上的李导数 ,对此我们做以下恒等式变换
现在仿照哈密顿矢量场的定义,我们可以定义 通过辛形式给出的矢量场
如此一来,
如果把上式按坐标展开,你会发现这正是我们熟悉的泊松括号,即泊松括号为 。如果我们取 ,那么代入上式,由于2-形式的反对称性,你很快就可以得到
即能量守恒。
相空间中的体积元取为
这个体积元在哈密顿矢量场方向的李导数不变,即
这则是刘维尔定理在相空间中的表述。
对于更详细的相关知识,读者可查阅[3][4](见文末)
四、总结
对哈密顿力学体系而言,物理状态是相空间中的某一点(一个元素),而物理态的演化轨迹则是相空间中的一条曲线,观测量则是相空间上的一个函数
以上便构成了经典力学的图像。
注释:
只需要广义坐标和广义速度就可确定系统的演化,而不需要广义加速度或是更高阶的导函数,这个事实原则上是实验告诉我们的,我们发现我们只需要广义坐标和广义速度就可得到系统的整个动力学演化结果。 这里的时间t应该看成是一个参数。 注意这里的矢量空间和对偶矢量空间是指相空间上的,而不是原来那个位形空间。 严格来讲给出的是局域解,不过在我们这的讨论也够了。 如果读者熟悉量子力学的话可以在这做一个很有趣的对比,在量子力学中,物理状态为Hilbert空间中的一个态矢,观测量则是一个自伴算子,由此可看出量子力学的确对于经典力学而言是一次革命性的发展。
参考资料:
[1] 朗道,栗弗席兹. 力学(第五版)[M]. 北京:高等教育出版社,2007
[2]梁昆淼原著,鞠国兴,施毅修订. 力学(下)[M]. 北京:高等教育出版社,2009
[3]阿诺德. 经典力学的数学方法(第四版)[M]. 北京:高等教育出版社,2006
[4]RALPH ABRAHAM AND JERR LE.MARSD. Foundations of Mechanics(second editon) [M] Canada:Addison-Wesley Publishing Company, 1987
对称性和守恒律
作者|胡竭末
简介
对称性在现代物理理论中非常重要,一般来说一个理论对称性越多,就越方便我们处理。
更进一步, 诺特定理(Noether's theorem)给出了(连续)对称性和守恒量之间的关系。
这是一个非常非常强大的定理。
本文的主要目的就是简要的介绍对称性和守恒律之间的关系。
整体对称性和诺特定理
我们首先来看最清晰也最简单的情形–––整体对称性。
设一个经典体系有拉式量,则作用量为
运动方程为
如果有一个整体变换
满足
那么我们就说这是一个整体对称变换。
对于连续的整体对称变换,我们可以取一个无穷小变换
满足
那么很显然我们有
假如有这么一个函数(微分形式),满足在边界上为0的边界条件。
那么我们由斯托克斯定理(Stokes' theorem)可知
这告诉我们,可以写为
可以看到以上的推导要求的是对称变换,但并没有要求满足运动方程。
现在如果我们要求一个无穷小变换保持运动方程,但并不要求保持作用量不变,这会发生什么呢?如下
因为我们已经要求满足运动方程了,所以上式第二行的第一项就为0,所以得
现在如果我们要求既满足对称变换,又满足运动方程,那么根据前式的对比可知
其中
所以就是一个守恒量,这就是诺特定理(有时候也叫做诺特第一定理)。
对于场论中的诺特定理推导是十分类似的,设
其中
为拉式密度,则
其中
总结一下,诺特定理告诉我们任何一个连续对称性有相应的守恒量。
特别指出的是,这里的对称性是针对有动力效应(dynamical)的变量而言的,对于属于背景(background)的量则没有以上的结果。
规范对称性
规范对称性(gauge symmetry)在现代物理理论中非常重要。
然而虽然我们把它叫做"对称性",但比较现代的观点是把它看成一种"冗余",它告诉我们描述不同物理的是一族数学上的等价类。
一个具体的例子为:在麦克斯韦理论中,如果电磁4-势为某个物理解,那么对于任何,描述的是与代表的同一个物理解。
我们首先来看一个玩具模型,考虑一个作用量
对于这个理论,存在这样一个对称性保持作用量不变
这个对称性对于完全没有任何要求,这和我们上一节提到的整体对称性有区别。
对于整体对称性而言,函数是被确定的,并没有这种任意性。
正因为对没有要求,所以每点处的可以不同,因此区别于整体对称性,我们把这种对称叫做规范对称。
运用运动方程,我们可得
我们发现这两个运动方程不是独立的,运动方程不能完全确定解的形式!
接下来如果我们直接利用诺特定理,你会发现
也就是说
规范对称性的守恒荷等于0!
这个结论不仅适用于我们这个玩具模型,而且是普遍结论。
我们不在这儿证明,但给出一点论述。
如果规范对称性带有可观测的荷,那么规范对称性就不再是一种冗余,而是代表了实际物理,因此守恒荷恒为0是很自然的结论。
为了能更好的看清规范对称性,我们现在转到哈密顿形式中去。
做勒让德变换(Legendre transformation),得
哈密顿量为
作用量则为
运用运动方程,我们会发现
这是个很不平凡的结论,它告诉我们(在满足运动方程的情况下)恒为0。
该怎么理解这种情况呢?
我们发现如果变量在拉式量中没有导数项,那么就不存在它的共轭动量,绝大多数我们熟知规范理论的哈密顿形式可以写成
的形式,从而可得
回忆一下高数中的拉格朗日乘子法(Lagrange multiplier),你会发现这跟我们这里的情形完全一样。
因此,我们把看成是一个乘子,而把看成是一个约束(在这个玩具模型中,约束即为)!因此我们可以说没有共轭动量的量通常是一个乘子。
本文并不打算继续叙述规范对称性和约束的关系,感兴趣的读者可以参考文献。
我们继续导出其他两个运动方程
再一次,我们发现这三个运动方程并不独立,因此不能完全确定解的形式。
对于具有规范对称性的理论,通常运动方程无法完全确定解的结果是规范冗余带来的。
因为运动方程描述的是物理的结果,而如今我们引入了冗余的"非物理"的信息,自然这部分多余的信息无法被运动方程确定,一般来说我们还需要额外的规范固定条件来确定最终的解。
小结
我们已经知道了整体对称性和规范对称性的不同。
作为一个例子,我们简单的对狭义相对论和广义相对论中的能量做个小论。
在狭义相对论中,时空具有时间平移不变性,这是一个整体对称性,因此我们可以借助这个对称性定义能量。
但在广义相对论中通常我们没有时间平移不变性,所以不能像狭义相对论那样定义能量。
由于等效原理,广义相对论有一个局域的微分同胚不变性,自然就可以有一个局域的时间平移不变性,这种不变性可以对应一个规范对称性,规范对称性对应的诺特荷恒为0,似乎是没有物理意义的。
但根据我们第二节的描述,我们应该把这种情况看成是一种约束条件,由此广相中的"能量"会有更复杂和丰富的内涵。
本文简单的介绍了经典理论中的对称性和诺特定理,我们得到结论
连续的整体对称性可导出守恒律。
规范对称性表达了一种冗余,通常会伴随某种约束。
对于量子化后的情况,本文按下不表。
参考文献
[1] M. Bañados and I. Reyes, A short review on noether’s theorems, gauge symmetries and boundary terms, International Journal of Modern Physics D 25 (2016) 1630021.
[2] A. Deriglazov, Classical mechanics. Hamiltonian and Lagrangian formalism, Classical mechanics. Hamiltonian and Lagrangian formalism (2010).
流形
作者|胡竭末
如无特别声明,本篇所取拓扑都为通常拓扑,即大家已经熟知的开区间和闭区间
笛卡尔将坐标的概念引入几何后大大方便和拓展了我们对几何的研究。
例如,对于一个圆,我们取坐标,这就描述了一个单位圆,利用这个表达式可以很方便地计算一些圆的性质。
但是如果把这个圆画出来,我们可能会感觉到有一点困惑,看上去圆似乎是“一条线”,为什么我们却需要两个坐标来描述呢?
或许你想到了用角度便可减少坐标(参数)到一个,可为了保证映射是一一对应的,你必须取的区间为,这不是一个好的选择,因为和这两点周边的性质是不同的,所以会给我们分析带来麻烦。
那怎么办呢?一个最简单的办法就是把这个圆分成多块,使得每一块可以由一个参数描述,并且这个参数的取值在的开区间上。然而这样的操作听上去这似乎割裂了整个圆,我们用这样的方式描述的圆还是原来那个吗?
事实上在很多时候,我们只关心一个点附近领域的性质,而不用管整个集合(上面这个例子中就是整个圆)的情况,因此这样的操作是可行的。
不但如此,如果我们要求不同区间上的映射满足一些条件,那么它甚至可以反映一些整体性质。
经历了上述并不简单的叙述,你可能会回到最初的疑问,我们是否真的需要将圆只用一个参数描述?我将它放到二维平面岂不是又直观又简洁?
的确,如果花费大力气改写我们已经很熟悉的语言,目的只是为了省点笔墨草稿,这大可不必,然而上述思考的过程中实际涉及了一个很深邃的问题,那就是我们可否在一个几何“内部”探索它本身?
让我来把话说得更清楚些吧。当你用到时,实际上你不但需要这个圆,你还需要整个平面(否则你没办法说这个方程代表了什么意思),然而当你用某段单参数区间来代指那个圆(的某一段)时,我们并不需要除了圆以外的东西,换句话说我们在内蕴的探究这个圆。
这不仅仅是数学思想上的一大进步,更是物理中的必然需要,因为我们生活在一个四维时空中,我们没有办法跳出这个时空到某个五维的空间中来观测我们自己的时空,所以我们必须寻找内蕴量来研究。
一、流形的定义
有了以上长长的铺垫,我们来看看具体该怎么构建符合要求的理论。
我们最熟悉的当然是维欧式空间,对于维欧式空间我们可以由一对数组来描述,我们要推广以上的概念,使得一个空间的局域部分长得像一个欧式空间,我们把这样的空间称为流形(manifold)。
如何来描述这种相似呢?
在第一章中我们介绍了拓扑的概念,拓扑给出了开集,利用开集我们可以定义连续,直观上我们马上就能想到连续和邻近领域是密切相关的,事实上你的确可以把拓扑看成是一种描述集合内各点“邻近关系”的结构,而同胚映射就是不改变这种“邻近关系”的映射。因此我们可以使用拓扑这个概念来描述一个空间局部类似于欧式空间。
在正式给出流形定义前,我们先定义什么叫豪斯多夫空间(Hausdorff 空间)
给定拓扑空间,如果任意不同的两点,总可以被两个不相交的开集分别包含,那么我们称这样的拓扑空间为豪斯多夫空间。
这种两点被不相交的开集覆盖的性质涉及到了拓扑空间的一个基本性质——分离性,由于分离性只依赖于开集的性质,所以它在同胚映射下不变,是一个拓扑不变量,对其感兴趣的读者可以自行翻阅拓扑教科书。
好,接下来让我们给出流形的严格定义
设是一个非空的豪斯多夫空间,并且满足第二可数性。如果对于每一点,都存在点的开集(开领域),使得同胚于的一个开集,同胚映射,那么我们称为一个维拓扑流形。
上述定义中的称为一张图(chart)或坐标卡,如果图的一个集合覆盖了,即,那么我们称这个集合为一个图册(atlas)。
以上定义中只是要求局部同胚于欧式空间,但此时我们仍然只有拓扑这一个结构,所以我们能用来使用的研究工具还是很少,接下来我们将引入一个极其重要的结构——微分结构。
考虑中的两个图,如果,那么中的点就有两套坐标,考虑这样的复合映射
或者
此时这两个映射就成了的映射,因此我们可以谈论这两个映射的光滑性。如果这两个映射都是的,那么我们称这两个图相关。
有了以上概念,我们可以定义微分结构
设是一个拓扑流形,如果满足以下三点
1.存在一个图册
2.图册中任意两个图是相关的
3.这个图册是极大的;也就是说,任何相关的图都已经被包含在这个图册里
这样我们就说给定了拓扑流形一个微分结构,我们把这样的流形称为微分流形,特别的,如果是,我们称其为光滑流形。
有了微分结构后我们就可以对流形进行微分,从而更方便的研究它。
技术上来说就是我们可以给流形上的点一个坐标,并且对这个坐标进行求导运算,之后如无特别声明,我们提到流形时都指微分流形,而且通常是光滑流形。
物理上我们通常是取在具体的坐标下进行操作的,我们以后的篇章大多也是如此,但重要的是当我们操作某个对象时,我们要很清楚我操作的对象到底是什么。
二、流形间的映射
两个流形分别为维流形,如果存在映射,对于点,两个流形上的坐标卡和,有复合映射
如果是光滑的,那么我们称在点是光滑的。如果它在每点都光滑,那么就在两个流形间定义了一个光滑映射。
在拓扑中我们知道了如果同胚那么拓扑性质就相同,现在我们多了一个微分结构,我们同样可以讨论怎样的情况下两个微分流形是相同的。
如果两个流形维数相同,而且存在一一映射,并且和它的逆映射是光滑的,那么我们称这是一个微分同胚映射
如果两个流形微分同胚,那么我们就没有办法在微分流形的角度区分它。
现在回过头去再看我们给出的光滑流形的定义,这个定义天然的给出了流形局部和欧式空间微分同胚(尽管我们在给出定义时还没有微分同胚的概念),也正因如此,我们可以用欧式空间的坐标来表征流形。
物理上通常要找不依赖于人为选择的量,因此物理量不应该取决于我们人为选择的坐标系,所以如果一个物理量背后的数学结构是流形的话,那么不同坐标系间的变换就应该是一个微分同胚映射。
三、小结
尽管我们花了不小的篇幅来把流形的概念严格化,但我们回过头会发现,去除冗长的定义,流形的思想是简单直观的。
也正因如此,流形的概念才会广泛地存在于各种物理理论中。接下来几章我们将给出流形上的一些基本的研究工具,如切向量,余切向量等。
拓扑空间如果有一个可数拓扑基,那么我们称其为第二可数的。之所以有这么个要求是因为豪斯多夫空间和第二可数性可以给出一个仿紧的性质,这个性质在我们定义单位分解,特别是流形上的积分时涉及到一个求和有意义的问题。不过我觉得这部分数学的构造性太强,离物理应用比较远,所以不打算详细说,我们会在讲流形积分时再浅尝辄止地提及,感兴趣的读者可以自行翻阅数学教科书。
拓扑
作者|胡竭末
拓扑是数学中非常重要的概念和工具,某种意义上来说拓扑之于现代数学就仿佛量子力学之于现代物理。我们会在本篇中给出拓扑最基本的概念,不过我们暂时并不会延伸这个话题,而仅仅只是为了给出接下来的篇章所需的最少的前置内容和概念。
一、拓扑的定义
设集合,集合的所有子集记为,称为幂集(power set)。我们挑选幂集中的某个子集,如果满足以下三个条件
空集和集合属于。
中有限个元素取交后的集合仍属于。
中任意数量元素取并后的集合仍属于。
则我们称给定了集合一个拓扑(结构),集合中的元素称为开集(open set)。
习惯上我们会把一个给定拓扑(topology)的集合称为拓扑空间(topological space)。
开集的补集称为闭集(closed set),但是注意一个拓扑空间里的集合可以既是开集又是闭集。事实上由开集和闭集的定义很容易看出来,任意拓扑空间里的空集和空间本身(也就上述定义里的)必然是既开又闭的。
选取不同的子集,就是定义了不同的拓扑结构。
例如,我们选取幂集(也就是说我们定义的所有子集都是开集),则我们就定义了一个拓扑结构,我们把这种拓扑叫做离散拓扑。
可以看出,离散拓扑空间中所有的集合都是既开又闭的。
当然我们也可以定义和为开集,其他的子集都不是。很容易验证,这样的选取也满足以上拓扑定义的规则,我们把选取U这样的拓扑称为连续拓扑。
你可以验证一下,通常意义上的开区间也满足拓扑的定义,所以这也是一种拓扑结构。
对于物理专业的学生来说,拓扑这个概念初接触时是非常抽象的,一个接受新概念的非常好的(如果不是最好的)方法是看一些例子。但很遗憾,由于拓扑实在过于基础,我们很难在现在直接给出一些帮助理解的例子。我觉得最好的方法是先接受它,然后继续学下去,慢慢的会习惯这种语言的。
二、同胚和连续映射
有了拓扑最基本的概念,我们来考察两个拓扑之间的关系即映射。
对于拓扑而言,重要的是它们的结构,也就是我们如何定义开集的。
那么很自然的,如果两个拓扑结构是“相同的”,我们就不需要重复处理,知道了一个就知道了所有和它“相同的”拓扑是怎么样的了。
为了严格描述这种相同,我们做如下定义
设有两个拓扑空间和,如果存在一个一一映射,将任意中的开集映到中的开集,将任意中的开集映到中的开集,那么我们称拓扑空间和是同胚的(homeomorphic),这样的映射称为同胚映射(homeomorphism)
同胚即代表两者在拓扑上不可区分,因此一些仅和拓扑有关的量在同胚映射下是不变的,但是如果一个量还依赖于其他结构,那么通常同胚映射不能保证这些量不变。
直到现在为止我们只是阐述了基本的拓扑是什么,但还没有拿它来做任何事情,接下来我们将使用拓扑来重新定义一个我们非常熟悉的东西——连续映射。
设有两个拓扑空间和,如果一个映射,对于中的任意开集,映射的拉回都是中开集,那么我们称这样的映射为连续映射
所谓的拉回就是映射在中的原像,所以连续映射就是保证开集的原像还是开集的映射。
读者们可以回忆一下高数里的连续的定义,本质上和我们用拓扑语言定义的连续是一样的,既然我们已经有了高数中的连续,那为什么又要用拓扑来重新定义连续这个概念呢?
一个重要的理由是从拓扑出发,我们能更方便的把连续这个概念推广到其他地方而不是局限在函数里。
三、拓扑的基
直接定义拓扑有的时候很复杂,因为直接定义需要你明确开集到底长成什么样,所以为了在一些情况下更方便的得到拓扑结构,我们定义拓扑的基
如果有一个拓扑,它的开集可以被一族子集里的元素取并得到,那么我们称这族子集为拓扑的基。
一个拓扑可以有不同的基,我不打算在这里展开拓扑基的相关内容,感兴趣的读者可以翻阅点集拓扑相关的书。
四、小节
我们已经例举了拓扑最基本的一点概念,但是我必须在这里停下了。接下来的篇章我们将介绍流形和流形上的一些概念,从实用的角度,这些内容将会对物理有更直接的影响和应用。
从卤蛋到小球:梳理相对性原理与协变性的关系
1. 隐秘的相对性原理
1.1 调皮的卤蛋
想象一个场景。
你坐在火车站候车室里,手机上翻着娱乐新闻渐觉没了意思,伸个懒腰恰好碰到身旁的碗装泡面。嗯······要不来一碗?于是,你开始撕包装,放佐料,倒开水,5分钟后,香味扑鼻而来。你小心翼翼地夹起圆润Q弹的卤蛋,正当送到嘴边时,一个滋溜,卤蛋竖直掉了下去,直直落入碗中,溅起油腻的汤汁,弄脏新买的衣服。
要向你推荐洗衣粉吗?不是的,其实我想问你:如果坐在匀速前进的火车上,重复上述操作——“撕包装,放佐料,倒开水,5分钟后,小心夹起卤蛋,正当送到嘴边时,一个滋溜,卤蛋竖直掉下去”,接下来会怎样?
A. 卤蛋仍然落入碗中,溅起油腻的汤汁;
B. 卤蛋缓慢落入碗中,汤汁平静无波澜;
C. 卤蛋漂浮半空,同桌目瞪口呆。
你可能会说:“你特么不是在逗我!情况显然和候车室里的一样嘛,选A。”恭喜,你发现了物理学中一条非常重要的原理——力学相对性原理。
其实早在1632年,伟大的物理学家伽利略就在《关于哥白尼和托勒密两大世界体系的对话》一书中,写到类似场景要表达的思想,只不过当时没有火车(1804年瓦特才造出了蒸汽机车),他用的是轮船。
伽利略认为:在一个匀速而封闭的船舱里,你看到单摆的摆动,水向瓶中滴落,虫子的飞行,鱼的游动等力学现象,和在地面上看到的没什么分别,也就是我们无法通过观察这些现象来区分船是静止的还是运动的。
用现代术语概括伽利略的这一思想就是:
一个对于惯性系作匀速直线运动的其他参考系,其内部所发生的一切物理过程,都不受系统作为整体的匀速直线运动的影响。
这就是力学相对性原理。怎么理解这句话呢?
相对性原理表达了两个深刻的内涵。
“为表述的直观和简洁,下文所提相对性原理皆指伽利略的力学相对性原理,不涉及爱因斯坦的狭义或广义相对性原理及洛伦兹变换。
”
1.2 相对性原理的内涵之一
第一个内涵是,我们无法通过各种力学现象(或力学实验)区分参考系是静止的还是做匀速直线运动。
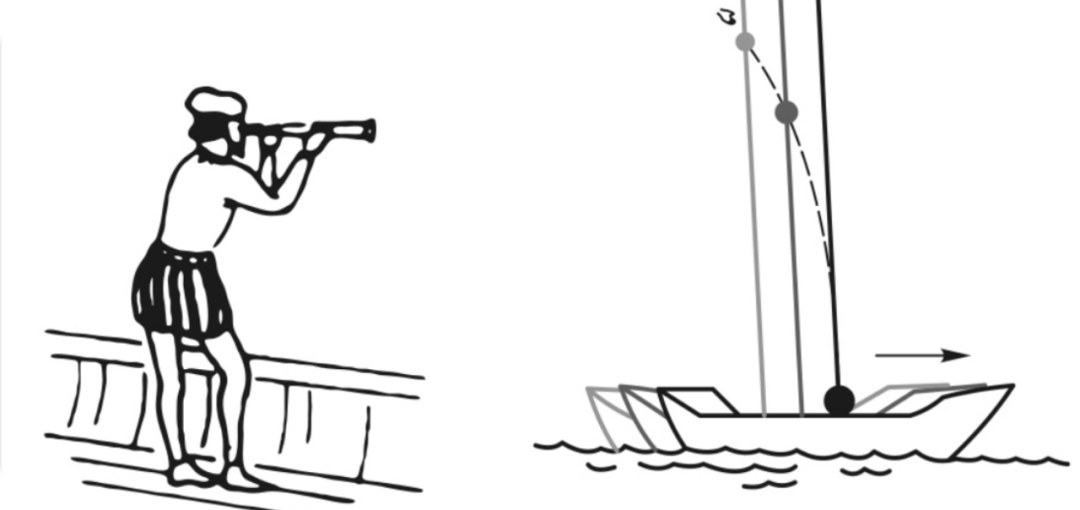
什么意思呢?比如下面这个场景,在没有看《泰坦尼克号》的情况下,你能分辨得出这段掀桌子事件是在船上发生的,还是在某个贵族的家里呢?

又或者,即使你知道这是在船上发生的,你还能通过桌子的翻转,茶碗的掉落,判断船是停在海上,还是朝着未知的礁石驶去呢?
嗯,想必你有感觉了。我们其实无法通过诸如桌子的翻转,茶饭的掉落等力学现象,去判断静止和匀速运动。你看,我们甚至连主角身在海上还是地面都搞不清楚。
似乎有点道理哈。
不过,当你从Rose惊诧的表情中回过神时,或许你会感到这好平常,好简单哦,简单到也没什么令人惊奇的呀?因为,如果桌子不这么翻,茶碗不这么掉,而是按照别的什么方式运动,那才叫诡异呐!
是的,相对性原理简单到理所当然,甚至不值一提。然而,正是这么简单的原理,却拯救了日心说,让日心说在地心说面前重新站起来,革新了人们对宇宙的认识,所以它真的很重要。
(关于相对性原理如何解开日心说的枷锁问题,详情可参阅长尾科技的文章《相对论前夜:牛顿和麦克斯韦的战争》)
另一方面,既然我们无法通过各种力学现象区分参考系是静止还是匀速直线运动,那么它俩其实没什么分别,干脆把它们统称为“惯性系”吧。这样,当以地面为参考系时,地面是惯性系,以匀速行驶的火车为参考系时,火车是惯性系。我们不再区分静止系和匀速系。概括地说:所有的惯性系平权。
1.2 相对性原理的内涵之二
第二个内涵是,对力学规律而言,一切惯性系都是等价的。
“爱因斯坦更进一步,不仅对力学规律,对所有的物理规律,一切惯性系都是等价的。
”
如果说第一个内涵告诉我们,在任何惯性系下做相同的事情(比如释放一个小球),它们的表现一样,第二内涵则告诉我们,不仅力学现象的表现一样,它们满足的力学规律也是一样的。
比如,你在海南从5米高处自由释放一个小球,约1秒落地,轨迹是直线,当你在夏威夷同样从5米高处自由释放小球,也约1秒落地,轨迹也是直线,不多一秒也不少一秒,轨迹更不会是曲线。为啥?因为它们一定满足相同的力学规律——自由落体公式。
万一在两地的落体公式有差异,人们将观察到小球不同的运动表现,类似卤蛋问题BC选项的诡异场景将会发生。万一在火车上或是轮船里,在乡间茅屋或是高楼大厦,人们看到的力学现象依赖不同的力学规律,那世界早就乱套了。
所以,力学规律在不同惯性系下一定要保持相同的数学形式。也就是说,力学规律要服从相对性原理。
关于相对性原理的讨论,我们就谈到这里,重要的结论总结如下:
①所有的惯性系平权。(谈的是惯性系)
②力学规律在不同惯性系下要保持相同的数学形式(谈的是力学规律)
让我们一睹发现这一重要原理的科学家——伽利略,然后开启新的探索。
2. 到别的惯性系耍耍
2.1 伽利略变换与协变性
我们已经知道,所有惯性系下的力学规律要相同,那么有个问题便会立马冒出来:
当科学家研究出一个力学规律,发现它在某一惯性系下成立,怎么才能知道它在别的惯性系里也成立呢?
由于力学规律主要研究力与运动的关系,那么,为了回答这个问题,得先思考另一个问题:我们是怎么掌握物体的运动状态的呢?
大致的操作一定是这样的:先观察和记录物体的时空坐标(即时间和空间的坐标信息),然后把时空坐标代入到一系列的物理方程中去,一通计算下来,就得到物体运动的完整信息,预测物体未来会怎么样。这里什么是至关重要的呢?
是时空坐标。因为若没有时空坐标,对运动的预测就成了无源之水,力学规律也将无从表述。
下面我们来看看时空坐标的表述。如下图所示,我们可以把质点相对于系的位置坐标和所处时刻记录为,它表达了质点什么时刻在什么位置,这就是时空坐标。
为讨论不同惯性系下的力学规律,我们自然要问:在别的惯性系里,质点的时空坐标又是多少呢?
比如说,在相对地面以速度匀速行驶的火车系里,质点的时空坐标与有什么关系呢?
伽利略告诉我们,他们满足下列关系:
这一组时空坐标的转换方式,被称为伽利略变换。它的意义在于,如果已知物体在某个惯性系下的时空坐标,通过伽利略变换,就能知道物体在别的惯性系下的时空坐标。它为两个惯性系搭起了沟通的桥梁,已知我的就能推知你的。(伽利略变换的推导过程非常简单,在任何一本普通物理教科书中都有提到,我就不复制粘贴了,感兴趣的朋友自行查阅)
“另外,如果在第一个式子两端分别对时间求导,我们还能得到两个惯性系下的速度变换公式:.
”
有了伽利略变换这座桥,我们就可以拿它检验物理规律是否服从相对性原理。
怎么检验呢?我们举个例子。
比如,在 系用时空坐标,加上物质的某些固有属性(像质量,电荷量什么的),分别定义了三个物理量,通过研究发现它们存在规律。
为了看系中的情况,我们对上面上个物理量施加伽利略变换,就得到了系中对应的三个物理量(要注意的是,它们物理意义与相同,但数值可以不同)。如果它们同样满足,也就是和系中的数学形式相同,我们就说这一物理规律在施加伽利略变换后具有协变性。协变的意思是,各个物理量协同起来一起变,使关系式仍成立。
所以,答案也就出来了。若物理规律在伽利略变换下具有协变性,它就不仅在一个惯性系下成立,在其他惯性系下也会成立,即服从相对性原理。
那么,日常生活中被广泛应用的力学规律,具有协变性吗?
2.2 牛顿运动定律具有协变性吗?
我们在小学二年级就知道,牛顿运动定律是所有力学规律的基石。所以,要想回答所有力学规律是否具有协变性,自然得先回答牛顿运动定律是否具有协变性。我们不妨以牛顿第二定律为例,证明一下。
牛顿第二定律的常见数学形式是。这三个物理量中,质量 是物体的固有属性,在不同惯性系下一定具有相同的值,是个不变量。外力 也是一个不变量,想想看,若在匀速运动火车系下用弹簧测力计竖直拉一个物块,弹簧伸长,显示拉力,在地面系看到的拉力也会是,力也是个不变量。
这样,为证明不同惯性系下牛顿第二定律的数学形式是否不变,就变成了看加速度在伽利略变换下是否保持不变。
在系中,加速度被表达为
在相对地面以速度 匀速运动的火车系中,利用速度变换公式,加速度就是
我们发现,火车系的加速度 跟地面系的加速度恰好一样。因此,牛顿第二定律在火车系和地面系具有相同的数学形式。
所以,牛顿第二定律具有协变性,也就表明了牛顿第二定律服从相对性原理。
要注意的是,不只是牛顿第二定律,牛顿力学的所有定律都具有协变性。证明方法和上面展示的类似,你可以尝试去做做。
总结一下:若力学规律在伽利略变换下具有协变性,它就不仅在一个惯性系下成立,在其他惯性系下也成立,即服从力学相对性原理。
3. 卤蛋给你智慧
虽然卤蛋弄脏了你新买的衣服,可它的美味让你回味无穷,你边吃边唠叨着:“具有协变性就服从相对性原理······具有协变性就服从相对性原理······吃卤蛋就要张嘴咯······那么······张嘴就要吃卤蛋吗?”
哎呀,这可是直达灵魂的一问!嗯,真是了不起的卤蛋。
我们在小学二年级就学过,若由可以推出,由却不一定能推出。既然物理规律具有协变性表明它服从相对性原理,那么反过来,服从相对性原理的物理规律,一定具有协变性吗?
为了回答这个问题,最好的办法莫过于找到一个例子,也就是找到一个物理规律,它虽服从相对性原理,但是不具有协变性。找哪一个呢?
要不先试试机械能守恒定律吧。
那么,机械能守恒定律服从相对性原理吗?
我们知道牛顿运动定律是服从相对性原理的,它就像获得上帝颁发的通行证,凭着伽利略变换,能在所有惯性系间畅行无阻。它又像一颗种子,把它种在毫无分别的土壤(惯性系)中,也一定能结出相同的果实。功能原理就是这众多果实之一,机械能守恒定律作为功能原理的一个推论,一定是服从相对性原理。
“在中学,机械能守恒定律被表述为:对系统而言,若除重力(或弹簧弹力)以外的力不做功,系统内只有动能和重力势能相互转化,总的机械能保持不变。
”
那么最关键的问题是,机械能守恒定律具有协变性吗?
4. 向实验要答案
呃······卤蛋面吃完了吗?要不把桌面收拾一下吧,我们得做点实验了。
虽然火车的餐桌没实验室里的方便,但足够应付接下来的实验了。目的就是,找到一个例子,使得机械能守恒定律在伽利略变换下不具有协变性。
“接下来会有一些数值计算,不是很难,请耐心看完,对随后的深入分析很重要。
”
4.1 "小球振一振"实验
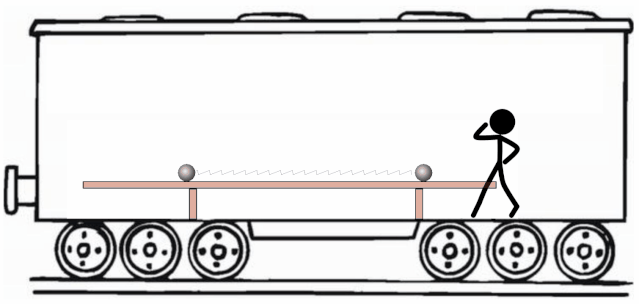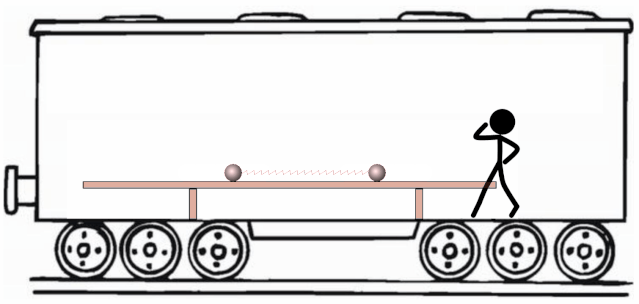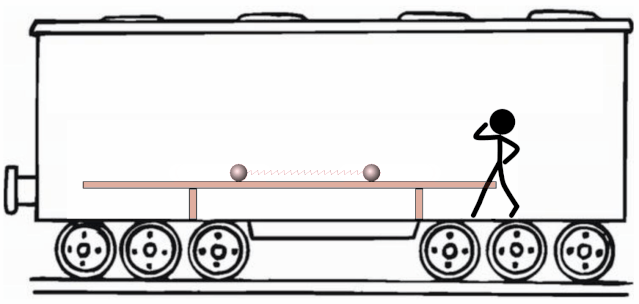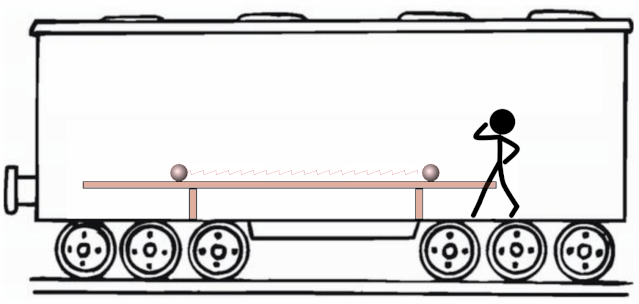
好的,桌面已经被收拾得光滑如镜了。你从旅行包里拿出一根轻弹簧(劲度系数
就像下面动图展示的这样。
4.1.1 火车系看"振一振"
把火车设为惯性系。不难发现, 弹簧双振子系统内除了弹力做功之外,没有其他力做功,系统的机械能一定守恒。在火车系,我们分别讨论弹簧处于最长和原长两个状态时系统的机械能情况。
弹簧最长时,俩球动能为,弹簧有弹性势能;
当弹簧原长时,弹性势能为,由机械能守恒,可以知道两小球此时的速度大小为,只是方向相反。
嗯,火车里的情况挺简单。我们再看地面系里会怎样。
4.1.2 地面系看"振一振"
把地面设为惯性系。假设火车相对地面的速度。我们同样去讨论弹簧处于最长和原长时系统的机械能情况。
弹簧最长时,由于变换惯性系不改变弹簧的长度,所以伽利略变换下的弹性势能依然是,但动能不一样,利用伽利略速度变换公式,易知俩球速度大小变成了,所以俩球的动能都为。所以此时系统机械能为;
当弹簧原长时,弹性势能为,跟火车系的一样。但是俩小球的速度,由于叠加火车速度的缘故变得不一样了,左小球速度为,右小球速度为。这样,俩小球的动能分别为,。此时系统的机械能还是。
4.1.3 "振一振"的结果
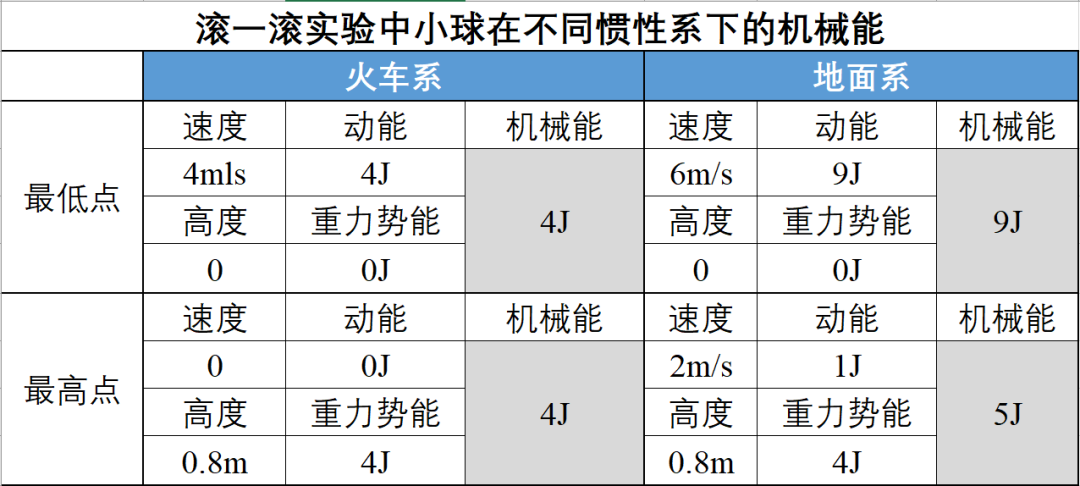
哎呀,计算发现,机械能在火车系是,地面系是,不同惯性系下虽然机械能的具体数值不一样,但在两惯性系下依然守恒,保持协变性。
但是请注意,我们的实验目标并没有达到,重申一下我们的目的,希望找到机械能在变换参考系后不守恒的情况。虽如此,但所谓失败是成功的妈妈,先把这个例子留着吧,说不定对接下来的分析有帮助呐。
4.2 “小球滚一滚”实验
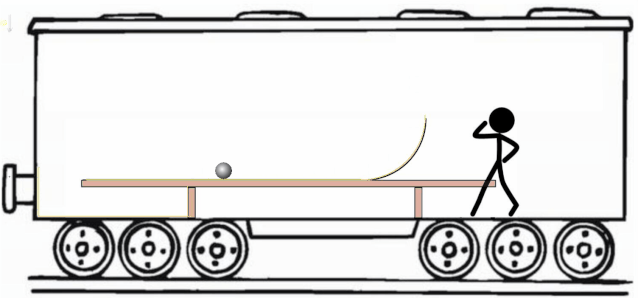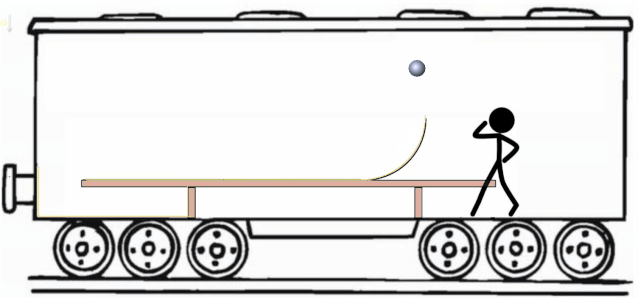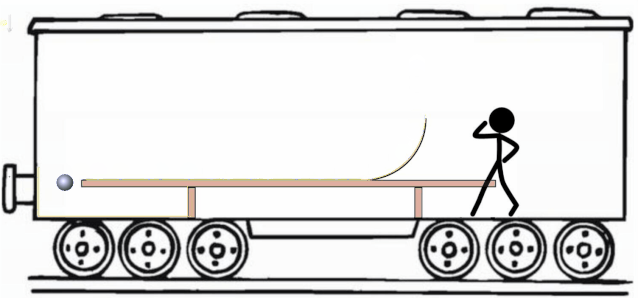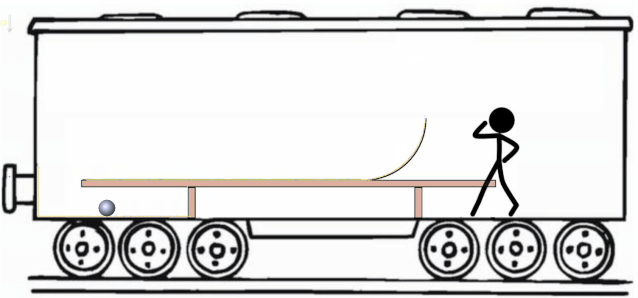
接下来我们改变策略。设计下面这个"小球滚一滚"实验,看看目标能否实现。
我们将一个光滑的的圆弧轨道置于桌面,与其平滑连接。相对与桌面,我们再给小球一个初速度,小球随后会冲上圆弧轨道。
我们再一次讨论火车系和地面系下,小球子在桌面和最高点的机械能分别是多少。
4.2.1 火车系看"滚一滚"
火车系的情况依然很简单。由于系统内只有重力做功,机械能当然是守恒的。(以桌面为零势能面)
小球在桌面时,动能为,若以桌面为零势能面,那么系统机械能就是。
当小球在最高点时,由机械能守恒 ,可求得小球上升的最大高度为。
4.2.2 地面系看"滚一滚"
现在转向地面系,情况会怎样呢?
小球在桌面时,由于叠加了火车的速度,小球速度变成了,动能相应地变为。而重力势能显然还是为零,所以系统机械能是。
当小球在最高点时,由于高度还是,所以重力势能是 。现在看在最高点的动能。小球虽然竖直速度为,但是在地面系的人看来,小球会有水平速度,所以动能为。这样,小球在最高点的机械能为。
4.2.3 "滚一滚"的结果
在小球滚一滚实验中,机械能在火车系是,而在地面系是。
啊哈!计算结果表明,对地面系的人看来,机械能守恒定律在伽利略变换下不具有协变性!
那么,你会兴奋地以为自己推翻了机械能守恒定律,或者断定机械能守恒定律不服从相对性原理吗?

5. 区分不同的问题场景
第一点:发现小球在地面系的机械能不守恒,不代表在地面系机械能守恒定律不成立。
为什么这么讲呢?因为某一系统的机械能具体为多少,以及在初末状态相不相等,跟机械能守恒定律本身成不成立是两码事。通俗地说,一个谈的是“事”,一个谈的是“规律”,"事"可以不同,但“规律“要相同。
比如下面这个场景。
船上的船员自由释放一个小球,他看到小球做自由落体运动,而岸边的人看到小球却做平抛运动。虽然运动状态不同,但是所满足的物理规律是一样的。你看,“事儿”不同,但“规律”相同。
所以,如果你想在地面系维护机械能守恒的尊严,只需要把"小球滚一滚"这个实验原封不动地搬到地面系再做一次就可以了。
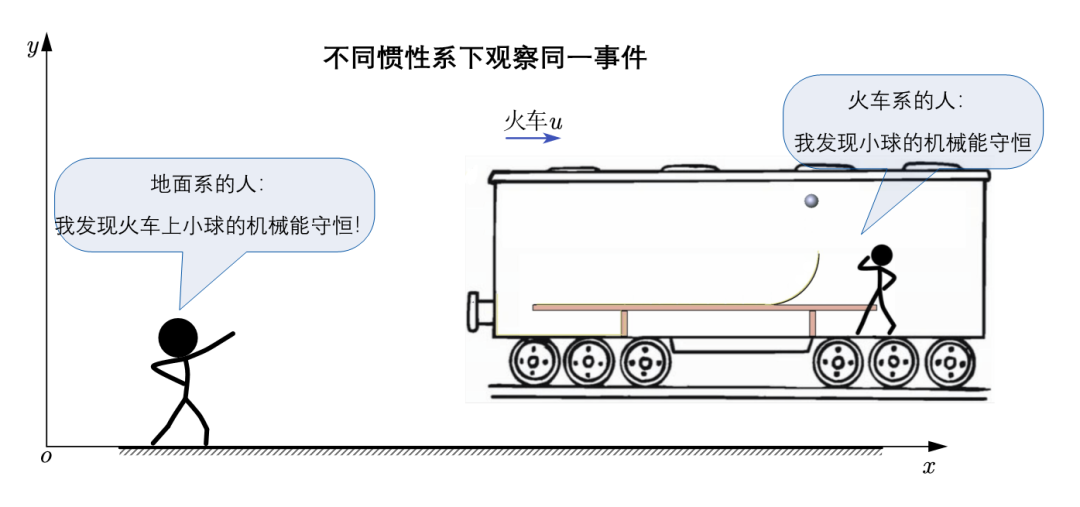
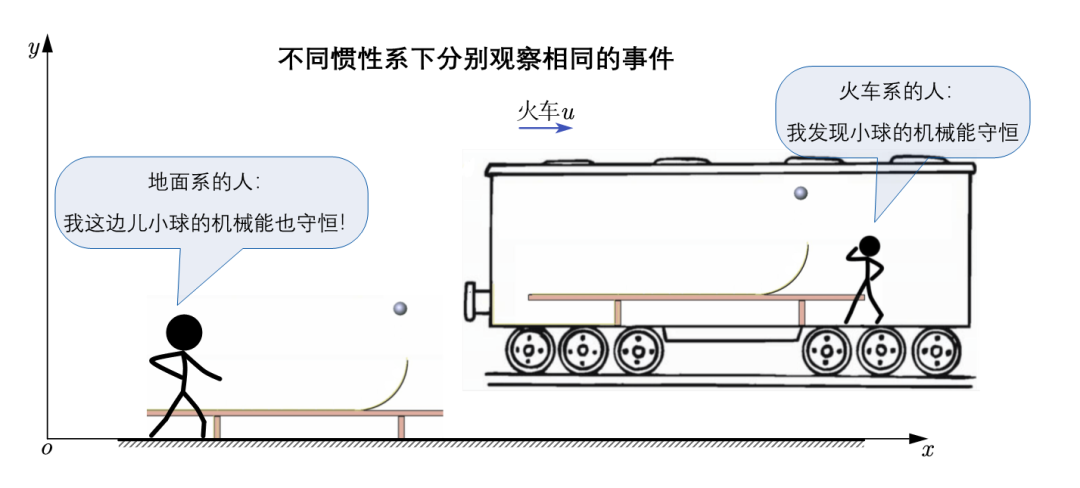
也就是要注意区分两类问题场景,一类是在不同惯性系下观察同一事件,另一个是在不同惯性系下分别观察相同的事件。请体会下边儿两张图的区别。
所以,当我们在谈某个物理规律是否具有协变性,以及是否服从相对性原理时,要注意我们谈的是“在不同惯性系下分别观察相同的事件,它们的物理规律相同”,也就是上图的第二个场景,而不是第一个。
6. 规律的条件可能不协变
回顾“小球振一振”与“小球滚一滚”两个实验,为什么在前一个实验中,小球的机械能可以在两个惯性系下都能保持不变,而在后一个实验中却不行呢?
原因还得从机械能守恒定律的成立条件上去找。
在“振一振”的实验中,两小球和弹簧构成的系统除了系统内弹力做功之外,其他的外力都不做功,不仅如此, 系统所受的合外力还为零!无论在火车系还是地面系观察,皆是如此。
反观“滚一滚”实验就不一样了。如下图所示,小球在冲上圆弧轨道的过程中,圆弧轨道对小球是有弹力的。对火车系来说,由于弹力始终与小球速度方向垂直,所以它对小球不做功,机械能守恒。
然而对地面系的人来说,小球由于叠加了火车的速度,使得小球的速度方向与轨道弹力的方向并不是始终垂直的,而是夹了个钝角,导致轨道弹力对小球做了负功。而这,恰恰就是地面系的人观察到机械能减少的真正原因。如下图所示。
对比两个实验,怎么才能在两个惯性系下都看到系统的机械能守恒呢?那就是不仅要使系统所受合外力不做功,而且连合外力为得为零,也就是系统得是完全“孤立”的,外界对它不能有一丁点儿的作用。很显然,这样的条件在日常生活中极为苛刻,因为几乎找不到绝对“孤立”的力学系统。
所以,若在别的惯性系下观察到系统的机械能不守恒,这事儿再正常不过了,没必要大惊小怪。
通过这两个实验,我们还可以知道,有些物理规律不具有协变性,是跟它的成立条件不协变有关的。比如“滚一滚”实验中,机械能守恒定律的成立的成立条件——合外力不做功——在火车系得到了满足,可是到了地面系就天然地不满足,也就导致了地面系观察不到小球的机械能守恒。
7. 相对性原理与协变性的关系
说了这么多,到了该总结的时候。我们已经知道,物理规律具有协变性就一定服从相对性原理,而服从相对性原理,却不一定具有协变性。
造成这种差别的原因又是什么呢?
其实,通过分析牛顿第二定律和机械能守恒定律这两个例子,答案已经出来了,关键是看规律的附加条件。
有些规律——比如牛顿运动定律——没有附加条件,它们往往更基本更普遍,对这类规律而言,具有协变性和服从相对原理是等价的。
而有些规律——比如机械能守恒定律——是有附加条件的(如初始条件、边界条件、规范条件等),这类条件通常不具有协变性,由此就导致了这些规律不具有协变性。而不具有协变性却仍然服从相对性原理,是由于这些规律本身蕴含在更一般的规律之中,可由这些更普遍的规律推导得出(如功能原理对于机械能守恒定律)。
讲到这里,我不由得想起了北京大学陈秉乾教授在讲库仑定律时说过的一句话:“物理规律是分层次的,上一层的规律要管着下一层的规律。”
那么,为什么普遍的物理规律要服从相对性原理,并具有协变性呢?它们有没有被某个上层的物理规律管着呢?
而这是另一个宏大的话题了,那就是科学家们绞尽脑汁要搞明白的守恒性与对称性,这是人类对美的终极追求。对这个主题感兴趣的朋友,可以看看长尾科技的另一篇文章《深度:杨-米尔斯理论说了啥?为什么说这是杨振宁超越他诺奖的贡献》
8. 旅程的结束
匀速的火车开始减速,我们的旅程也即将到达终点。从调皮的卤蛋到小球的实验,我们讲了很多东西:
从相对性原理的内涵到伽利略变换与物理规律的协变性,我们了解到,上帝并不偏爱某一特殊的惯性系,上帝是最公平的存在。
从卤蛋带给我们的思考到向实验要答案,我们发现,有些命题正着说成立,反着说却不一定成立,从正反两个方面去思考问题,恰恰能让我们对规律的认识更加深刻而明晰。也正是由于这个思考让我们知道,不要试图把协变性与相对性原理捆绑在一起,它们并不是互为充要条件的。
9. 参考文献
感兴趣的朋友若想从理论高度深入了解力学相对性原理与协变性的关系,可以看看下面列出文献,尤其是形成结论的文献[1] [2] [3] [4] [5]。
[1] 赵凯华.澄清对相对论性原理和协变性的误解[J].大学物理,2020,39(01):12-13. [2] 编者的话[J].大学物理,2002(03):18. [3] 朱如曾.相对性原理对普遍定律和非普遍定律参考系变换性质的不同要求——关于协变性疑难的进一步讨论[J].大学物理,2002(03):19-23. [4] 朱如曾.相对性原理及其对自然界定律的协变性要求——机械能守恒定律协变性疑难的解答[J].大学物理,2000(02):15-19+26. [5] 喀兴林.编者的话[J].大学物理,2000(02):27-29+34. [6] 高炳坤.“机械能守恒定律是否遵从相对性原理”辨[J].大学物理,2000(02):20-22. [7] 高炳坤.机械能守恒定律和相对性原理[J].大学物理,1999(01):3-5. [8] 蔡伯濂.“关于力学相对性原理与机械能守恒的来稿综述[J].大学物理,1994(01):20-22. [9] 管靖.力学相对性原理与机械能[J].大学物理,1991(11):21-24. [10] 赵凯华.新概念物理教程力学[M]北京:高等教育出版社,2004.
致谢
本文在修改中得到一些网友真诚而且重要的意见,特别是Core、长尾逍遥、一夜星辰、强电弱电那些事、暖球、晨曦,向你们表示由衷地感谢。



最美丽的物理学实验









美的不同方面

公平竞争

Slashdot网站的讨论

单电子的杨氏双缝干涉实验 Young's double-slit experiment applied to the interference of single electrons 伽利略的落体实验(1600年代) Galileo's experiment on falling bodies (1600s) 密立根的油滴实验(1910年代) Millikan's oil-drop experiment 牛顿的棱镜分光实验 (1665-1666年) Newton's decomposition of sunlight with a prism 光的杨氏双缝干涉实验 (1801年) Young's light-interference experiment 卡文迪什的扭秤实验 (1798年)Cavendish's torsion-bar experiment 埃拉托色尼(Eratosthenes)测量地球的周长 (公元前3世纪)Eratosthenes' measurement of the Earth's circumference 伽利略的斜面实验(1600年代) Galileo's experiments with rolling balls down inclined planes 卢瑟福发现原子核的散射实验 (1911年) Rutherford's discovery of the nucleus 傅科的钟摆实验 (1851年) Foucault's pendulum
阿基米德的流体静力学实验 Archimedes’ experiment on hydrostatics 罗默测量光速的实验 Roemer’s observations of the speed of light 焦耳的热功当量实验 Joule’s paddle-wheel heat experiments 雷诺的层流实验 Reynolds’s pipe flow experiment 马赫和萨尔克(Salcher)的冲击波实验 Mach & Salcher’s acoustic shock wave 迈克尔逊-莫雷的以太实验 Michelson-Morley measurement of the null effect of the ether 伦琴测量麦克斯韦位移电流的实验 Röntgen’s detection of Maxwell’s displacement current 奥斯特发现电磁现象的实验 Oersted’s discovery of electromagnetism 布拉格父子的X-射线散射实验 The Braggs’ X-ray diffraction of salt crystals 爱丁顿测量星光弯曲的实验 Eddington’s measurement of the bending of starlight 斯特恩-盖拉赫的空间量子化实验 Stern-Gerlach demonstration of space quantization 薛定谔猫思想实验 Schrödinger’s cat thought experiment 核连锁反应的三位一体实验 Trinity test of nuclear chain reaction 吴健雄等验证宇称不守恒的实验 Wu et al.’s measurement of parity violation 戈德哈伯的中微子螺旋性实验 Goldhaber’s study of neutrino helicity 费曼的O圈实验:Feynman dipping an O-ring in water

双缝实验的美丽之处

美和实验过程

临界点







有史以来最伟大的方程

本文译自Robert P Crease所撰写的The greatest equations ever一文,发表在Physics World, 2004, 17(10):14–15上,为同年5月份作者请读者为“有史以来最伟大的方程”的投票结果。因为看到网上有不同的版本,特意翻译出来分享。特别的是,作为教授电动力学的老师,怎能容忍其他方程排在麦克斯韦方程组的前面(嘿嘿!)。翻译目的为分享知识,欢迎指正。如有侵权,请告知删除。点击文末原文链接可以阅读英文原文。



今年早些时候,我请读者把他们心目中的伟大方程的名单发给我。我还请他们解释为什么他们提名的方程属于伟大之列,并且如果有的话,为什么方程所涉及的主题很重要(Physics World,5月刊,第19页)。我收到了大约120份回复—包括单个候选方程和方程名单—其中推荐了大约50个不同的方程。这些方程包括从显而易见的经典方程到“被忽视”的候选方程,从个人喜好到被调查者自己发明的方程。
有几个人询问了公式、定理和我所谓的方程之间的区别。一般来说,我认为公式是遵循句法规则的东西。从这个意义上说,是一个公式,而也是。相反,定理是从更基本的原理中得出的结论—毕达哥拉斯定理就是一个很好的例子。严格意义上的方程通常是一个公式,它说明所观察到的事实,因此从经验上来说是正确的。描述可见光谱巴尔末线系(Balmer series)的方程是一个很好的例子,体现实验室中观察到的反应的化学方程也是一个很好的例子。
然而,这些区别其实并不那么清晰。许多经典的物理方程—包括和薛定谔方程—都不是从关于观察的表述中得到的结论。相反,它们是基于其他方程和信息推理得出的结论;因此它们更像定理。定理可以像方程,因为其具有很强的经验成分和价值。
因此,将这两种归类为方程是有意义的,这正是曼彻斯特大学的被调查者David Walton所做的。他区分了由公理模型构成的方程(如)和近似模型(如胡克定律)构成的方程,公理模型“定义了所有情况下不同的可观测值之间的相互关系”,而近似模型则定义了“定义范围内在一定精度下不同的可观测值之间的相互关系”。因此,我对“方程”一词的解释是宽松的。



简单
被调查者有许多不同的标准来衡量方程的伟大。半打人(Half a dozen)对方程的简单印象深刻,他们推荐了 。
加拿大卡尔加里(Calgary)的Richard Harrison写到:“我知道其他方程做得更多,表达了更强大的力量,对宇宙有更广泛的理解,” “但是最简单的那种事物的美是值得一提的。” 他回忆起他教儿子的第一个方程是。“我记得(他)在学习这个表达式的时候举起两只手的食指,以及当他看到被全身分开的两个手指可以在脑海中结合成一个概念时那惊奇的一刻。”
Neil Blackie也支持。“为了使这个方程得以存在,必须发明一种表示物理现实的方法,数量必须被命名和给予符号,” 他论证到。“必须有一个体系来显示这些数量是如何组合在一起或分开的。写下这个方程使我们有能力呈现想法,讨论概念,从而形成一个不断扩大的知识领域。”
其他被推荐的简单方程包括,这是埃德温·哈勃(Edwin Hubble)在1929年提出的,它用来描述星系以一定的速度远离我们,这个速度与星系间的距离成正比,其中是哈勃常数。位于马其顿斯科普里的物理研究所的本科生Balagoj Petrusev推荐形式的哈密顿变分原理。对形式的恰当选择清楚地表明“在经典力学、经典电动力学、相对论力学、非相对论量子力学等领域都适用的普遍原理”。事实上,肯特大学的Andy Hone上个月在Physics World上写了了一篇赞颂这个方程的文章(9月刊,第64页)。
一个伟大方程的统一力量并不像听起来那么简单。一个伟大方程所做的不仅仅是阐述宇宙的一个基本属性,像路标那样传递信息,而是努力从自然那里获取什么。如布里斯托尔大学的Michael Berry曾经谈到电子的狄拉克方程时说道:“任何伟大的物理理论的回馈都大于投入,其意义在于除了解决激发方程被构建的问题外,它还解释了更多的现象,并预言新的事物”(Physics World,1998年,2月刊,第38页)。
伟大的方程改变了我们感知世界的方式。它们重新编排了这个世界—通过重新定义什么应该与什么在一起改变并重新整合了我们的观念。光和波。能量和质量。概率和位置。而它们这样做的方式往往显得出人意料甚至奇怪。
基于这个原因,一些被调查者推荐了一些方程,它们联系两个或两个以上不同的概念,具体和抽象的,有形的和无形的。其中包括玻耳兹曼方程。它把熵(19世纪早期热力学发展过程中出现的概念)和一个纯粹抽象的量联系起来(是在对具有许多自由度的系统的统计处理中出现的)。另一位被调查者写道,布拉格方程 “将衍射斑(可见的现实)与潜在的晶体结构(不可见的现实)联系起来,用标准教科书上的图片就很容易进行想象。”
最常提到的方程之一是欧拉方程。被调查者称之为“有史以来最深刻的数学表述”;“不可思议和令人赞叹”;“充满宇宙之美”和“令人震憾”。另一个被调查者问道:“有什么比一个虚数和实数相互作用而不产生任何东西更神秘呢?“ 这个方程中包含九个基本数学概念—一次且仅一次在一个表达式中。这些概念是:(自然对数的底);指数运算;;加法(或减法,取决于你怎么写);乘法;虚数;等于;一;和零。

实用性
许多被调查者对那些对人类生活有实际影响的方程印象深刻。这些方程包括:复利 (compound interest) 方程,其意义从文艺复兴到现在是“明显的、惊人的和不受欢迎的”;所得税公式;简单的比例 ,这是建筑、测量等的基础;简单的电学方程,如;基本的力学方程,如功=力×距离;香农容量(Shannon’s capacity)方程,它通过互联网和数字通信与现代世界联系在一起;最后但同样重要的是,毕达哥拉斯定理(Pythagoras’s theorem)。
Roger Bailey提名了“日出方程”cos(time) = –tan(lat)×tan(dec),它将日出或日落的时间确定为纬度和太阳赤纬(solar declination)的函数。他指出,这是“我们时间感的基础”,它“适合印在T恤衫上”。工程师John Wilcher推荐理想气体定律,,指出“压力、体积和温度的关系几乎与我们所做的一切都相关”,包括常见但常常被忽视的用途,如汽车轮胎、血管成形术和石油钻探。
同时,加拿大萨斯喀彻温(Saskatchewan)大学动物农业名誉教授Iain Christison推荐—代谢能量等于热量加产品。这个方程描述了这样一个事实:“包括人类在内的动物所消耗的所有有用的能量都以热量的形式释放或以产品的形式储存。”。他补充说,这个等式“包含着错综复杂的因果平衡,影响着我们每一个人的每一口饭和每一步行动”。

历史相关性
一些被调查者推荐了在科学史上起到关键作用的方程。例如,Alan Denham推荐了巴尔末线系方程。这个方程的悠久历史可以追溯到1814年夫琅禾费对太阳光谱的研究,到1859年基尔霍夫提出每种原子都有一个独特的光谱,到1868年Angstrom发布了一千条夫琅禾费谱线的波长,再到1885年中学教师约翰·巴耳末(Johann Balmer)注意到氢原子发出的光的频率在数学上是相关的。这个公式的历史被莱曼在紫外线区和其他人在红外区的观测、被里德堡(公式中的常数因他得名)和波尔(他在1913年的工作解释了这个公式)所延续。波尔曾说:“我一看到巴耳末的公式,整个事情对我就立刻明朗了。“
"因此,这个长达一个世纪的故事,“ Denham写道,“涉及到一些最杰出的实践者对科学的理论和实践研究,如果对一位中学教师的贡献不给予应有的荣誉,这将是不完整的,他发现所发表的科学数据符合当时所有科学家都不知道的一种模式。”

最伟大的20个方程
下面的方程是按照所推荐的人数顺序列出的。在大约120个推荐中前两个方程收到了约25个,其余的方程收到了2到10个不等的推荐。方程视情况以最常见的形式给出。
麦克斯韦方程组:
其中,是电位移矢量,是电场强度,是磁感应强度,是磁场强度,是自由电荷密度,是自由电流密度。
欧拉方程:
牛顿第二定律:
毕达哥拉斯定理:
薛定谔方程:
质能方程:
玻尔兹曼方程:
1+1 = 2
最小作用量原理:
德布罗意方程:
傅里叶变换
广义相对论的爱因斯坦场方程:
圆的周长:
狄拉克方程:
欧拉的另一个方程:
哈勃方程:
最简单的比例:
理想气体定律:
巴尔末线系:
普朗克方程:

麦克斯韦方程组
这些回答表明,没有一个衡量伟大的单一标准,而一个真正伟大的方程在上述每一个标准中都应名列前茅。然而,大多数人投票赞成欧拉方程和麦克斯韦方程组,后者描述了电磁场在空间和时间上的变化。虽然麦克斯韦方程组相对简单,但它们大胆地重构了我们对自然的感知,统一了电和磁,并将几何、拓扑和物理联系起来。它们对了解周围的世界至关重要。作为最早的场方程,它们不仅向科学家们展示了一种新的处理物理的方法,而且还使科学家们朝着统一基本自然力的方向迈出了第一步。佛罗里达州一家名为海洋光学(Ocean Optics)的公司甚至销售印有麦克斯韦方程组的T恤衫。
Tony Watkins回忆起差不多20年前在南安普顿大学读本科二年级时是如何学习这组方程的。他写道:“我至今还清楚地记得,有一天我学习了麦克斯韦方程组的矢量记法。” “这四个方程能描述这么多,真是非同寻常……我第一次理解了人们在谈论数学或物理学中的优雅和美丽时的含义。它激动人心,是我本科生涯的转折点。经过一年对物理学的兴趣迅速减少(成绩也迅速降低!),这四行符号重新点燃了我的激情。” 他甚至把他的下一辆自行车改名为麦克斯韦,以纪念这位伟人,因为他以前骑过”卡诺循环“自行车。可惜的是,他从来没有抽出时间去学习张量,那样的话可以看到麦克斯韦方程组表达得更简洁。

临界点
没有人接受我的邀请去讨论为什么方程中的伟大很重要,这让我自己可以自由地讨论这个话题。就这个问题进行辩论有缺点,因为它可以助长这样一种观念,即方程是独立的工具,而不是融入到其他方程、实践和信息的关系网中。然而,这有助于我们回忆起除了其他内容外Richard Harrison所说的“奇迹时刻”,而“奇迹时刻”在他儿子陷入对的沉思时是显而易见的.
作为成年人,我们失去了这种奇迹。我们开始把方程看作是世界上手头现成的另一套工具。我们失去了对其来源的欣赏,认为它们不是出自人类之手:在第八天,上帝创造了方程作为他最近工作的蓝图。正如伽利略所写的—虚伪地,有争议地—自然之书是用数学符号写的。当然,那不是真的。我们写并不断地重写着自然之书。
正如哲学家伊曼努尔·康德((Immanuel Kant)曾经写道:“当我们发现两个或两个以上各种各样的的自然经验规律可以统一在由它们组成的一个原则下时,这一发现的确会带来一种明显的愉悦……甚至赞赏,而当我们对它的对象相当熟悉时,这种赞赏也不会停止。” 这种喜悦不仅仅是让我们的期望得到满足或惊喜,不仅仅是对大自然的支配和控制,也不仅仅是一种生物产品。康德继续说,这种愉悦是人类智力活动的一个特征。他写道:“没有它,即使是最普通的经验也是不可能的,” 这就是为什么我们 “逐渐地把它与单纯的认知混在一起,不再对其特别注意。”
在重新唤醒那种奇迹感的过程中,辩论什么使方程伟大使我们重新学习科学的基本性质和知识本身。








光学前沿—光子纳米喷射

本文译自Alexander Heifetz等所撰写的Photonic Nanojets一文,文章发表在Journal of Computational and Theoretical Nanoscience, 2009, 6(9):1979–1992上。此文为本科毕业设计任务所翻译题目,目的为分享知识,欢迎指正。如有侵权,请告知删除。点击文末原文链接可以阅读英文原文。


本文回顾了自2004年以来有关光子纳米喷射的主要文献。光子纳米喷射是从被照射的直径大于波长的无损介质微柱或微球的阴影面后出射的狭窄、高强度的光束,它是一种非倏逝波并可以传播超过波长的距离。纳米喷射的最小束宽可以小于经典衍射极限,对于微球来说,实际上束宽可以小至。当其折射率与背景折射率之比小于约2:1时,在微柱或微球大范围的直径范围内会出现光子纳米喷射这种非共振现象。重要的是,在纳米喷射中放置直径为
的纳米粒子会使被光照射的微球的远场背向散射功率受到扰动,在固定波长下其扰动量随变化。对于同一孤立的纳米粒子,这种扰动比按照变化的瑞利散射要慢得多。这导致了这样一种情况,例如,如果将直径为的纳米粒子放入到由直径为的微球产生的纳米喷射中,尽管纳米粒子的截面面积仅为微球的万分之一,测量到的微球远场散射功率可以达到原先的两倍。实际上,纳米喷射的作用是将纳米粒子的存在投射到远场。这些特性结合在一起,使得光子纳米喷射在检测和操纵纳米量级的物体、超衍射分辨率纳米图案成形和纳米光刻、低损耗波导和超高密度光学存储等方面具有潜在的重要应用价值。

1. 引言
自2004年以来,出现了大量关于光子纳米喷射的存在、性质和潜在应用的大量文献1–20。光子纳米喷射是从被平面波照射的直径大于入射波长的无损介质微柱或微球的阴影面后向背景介质中传播的狭窄、高强度的电磁波。光子纳米喷射的主要特性包括:(1)它是一种非倏逝的传播波,在介质柱或球外延伸超过的路径上其半高全宽(FWHM)的横向光束宽度可保持在亚波长。(2)它的最小FWHM束宽可以小于经典衍射极限,对于微球来说,实际上束宽可以小至。(3)当介质折射率与背景折射率之比小于约时,在微柱或微球的直径处于到的大范围内会出现光子纳米喷射这种非共振现象。(4)它的强度很高,大大超过入射光强度。(5)在纳米喷射中放置直径为的纳米粒子会使被光照射的微球的远场背向散射功率受到扰动,在固定波长下其扰动量随变化。对于同一孤立的纳米粒子,这种扰动比按照变化的瑞利散射要慢得多。这导致了这样一种情况,例如,如果将直径为的纳米粒子放入到由直径为的微球产生的纳米喷射中,尽管纳米粒子的截面面积仅为微球的万分之一,测量到的微球远场散射功率可以达到原先的两倍。实际上,纳米喷射的作用是将纳米粒子的存在投射到远场。这些特性结合在一起,使得光子纳米喷射在检测和操纵纳米量级的物体、超衍射分辨率纳米图案成形和纳米光刻、低损耗波导和超高密度光学存储等方面具有潜在的重要应用价值。本文综述了迄今为止纳米喷射领域的研究进展,旨在推动纳米喷射方面的研究。本文讨论的内容包括:介质柱光子纳米喷射的最初确定(第2节);介质球光子纳米喷射的最初确定(第3节);光子纳米喷射理论(第4节);实验观察(第5节);以及潜在的应用(第6节)。
2. 介质柱光子纳米喷射的最初确定
Chen等人1最初将光子纳米喷射确定为一种独特的电磁波类型,并创造“光子纳米喷射”这个术语来描述它。利用高分辨率的时域有限差分算法(FDTD)求解麦克斯韦方程组,21 证明当一平面波照射微米尺度的介质圆柱时,会产生一个狭窄、高强度、束宽低于衍射极限的光束,从微柱的阴影面向背景介质中传播。报告进一步指出,当在纳米喷射内放置一纳米尺度的介质圆柱时,产生纳米喷射的微米尺度介质柱的背向散射功率会受到巨大的扰动。也就是说,扰动比孤立的纳米圆柱的背向散射大几个数量级。
文献[1]首先回顾了FDTD算法的验证,采用了大小为的均匀方形网格(在所有模拟运算中比波长的还要精细)和网格外围的完美匹配层吸收边界条件。21 通过将用FDTD计算的几种均匀、各向同性的介质圆柱的微分散射截面和精确级数解作比较,发现在的动态范围内研究的所有情况下,整个散射角范围内误差在 以内。
文献[1]接着报道了对一列均匀、各向同性、无损、无限长的介质圆柱的内部和近外部场的详细的二维计算研究。假定每一个圆柱都被入射电场与圆柱无限长轴平行的平面波照射。图1显示的示例结果说明了光子纳米喷射随介质圆柱折射率减小的演化过程。这里显示了FDTD计算的正弦稳态电场的包络,所研究的结构为放置在折射率的无限真空介质中的直径为、均匀折射率为的圆柱。波长为的光在介质2中从左向右传播。当从图1(a)中的降至图1(b)中的时,圆柱内部电场峰值向阴影面移动。进一步把降至图1(c)中的时,电场峰值从圆柱的阴影面出现,呈强喷射状分布,长度为,FWHM强度束腰为略低于衍射极限的 。这种从的圆柱阴影面出现的喷射和以前关于光学焦散的研究工作是一致的。22, 23

图1 光子纳米喷射随被平面波照射的介质圆柱折射率减小发生的演化过程的演示。显示了FDTD计算的正弦稳态电场的包络,所研究的结构为放置在折射率的无限真空介质中的直径为、均匀折射率为的圆柱。波长为的光在介质2中从左向右传播。(a) ;(b) ;(c) 。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。

文献[1]接着报道,如果的值相较于图1(c)中的值不发生显著变化,那么类似于图1(c)中的束腰略小于衍射极限的光子纳米喷射可以通过、、和的不同组合来产生。图2给出了多个例子:(a) ,,,;(b) ,,,;(c) ,,,。包括图1(c)的情况,所有模拟的纳米喷射的FWHM强度束腰范围在到之间,长度在到之间。
最后,通过FDTD模拟,文献[1]考虑了将起扰动作用的纳米级介质柱置于微米级主柱产生的纳米喷射中带来的影响。测试使用了图2(b)中的参数,即一个直径为、折射率为的主圆柱放置在折射率为的无限外部介质中,照射光波长为。假设扰动纳米介质柱具有边长为的方形截面,且其折射率为。在FDTD模型中,该纳米柱被放入直径为的主柱表面的光子纳米喷射的中心。
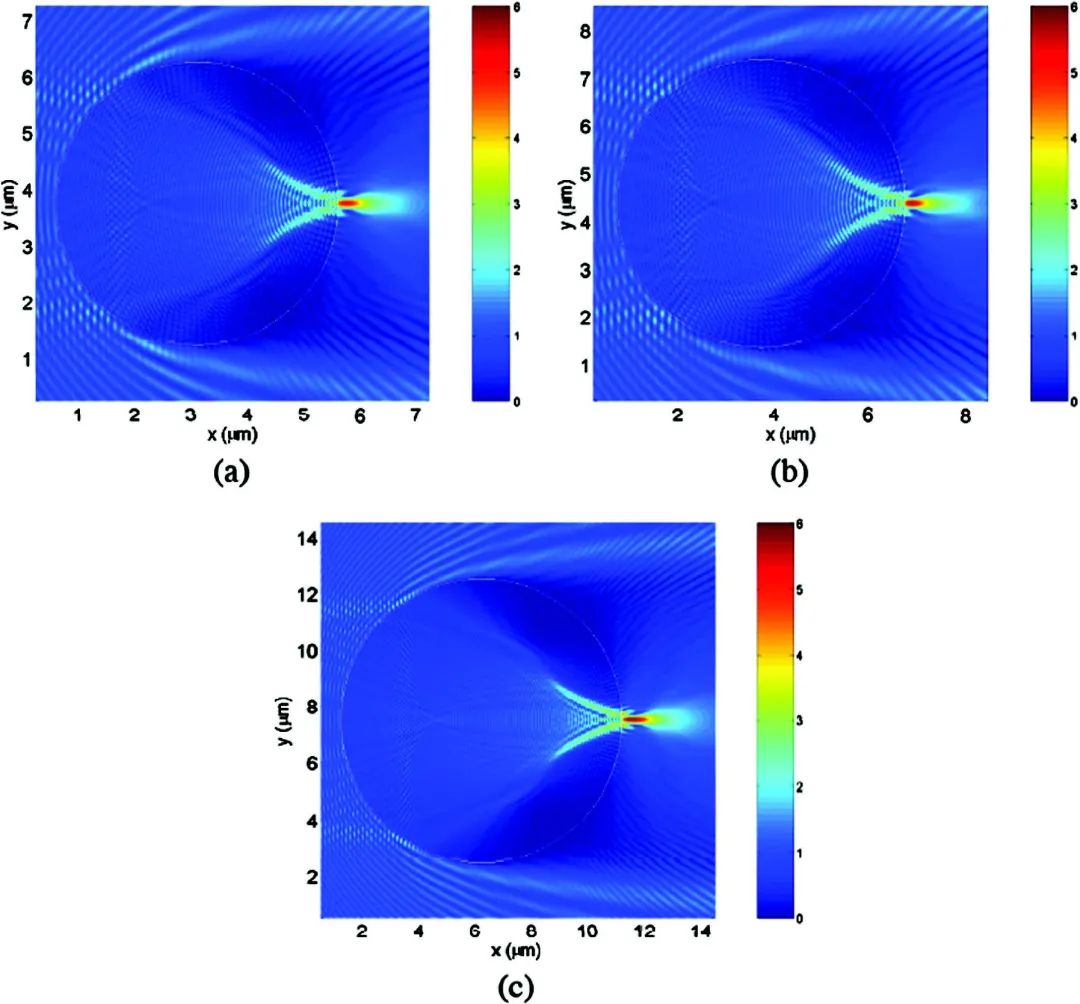
图2 与图1(c)中类似的、、和三种不同组合所产生的光子纳米喷射的演示。(a) ,,,;(b) ,,,;(c) ,,,。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。

图3(a)绘制了在背向散射范围内主微柱的微分散射截面受到的扰动的绝对值。此图还绘制了对应的被平面波照射的孤立扰动纳米柱的微分散射截面。这些结果表明,位于纳米喷射中的的介质纳米柱对微柱的直接背向散射截面的扰动大约是孤立纳米柱背向散射的倍。图3(b)给出了文献[1]中额外的FDTD模拟结果,表明当
减小到以下时,扰动纳米柱背向散射的有效增强(用表示)单调增加,且当时达到大约的水平。
基于以上计算模拟的结果,文献[1]总结到,光子纳米喷射可能会提供一种检测尺寸远低于经典衍射极限的纳米粒子的新方法。这有潜力为如下应用提供新的手段:使用可见光检测蛋白质、病毒粒子甚至单个分子;监测在生物学、化学、材料科学和组织工程许多领域具有重要意义的分子合成和聚集过程。
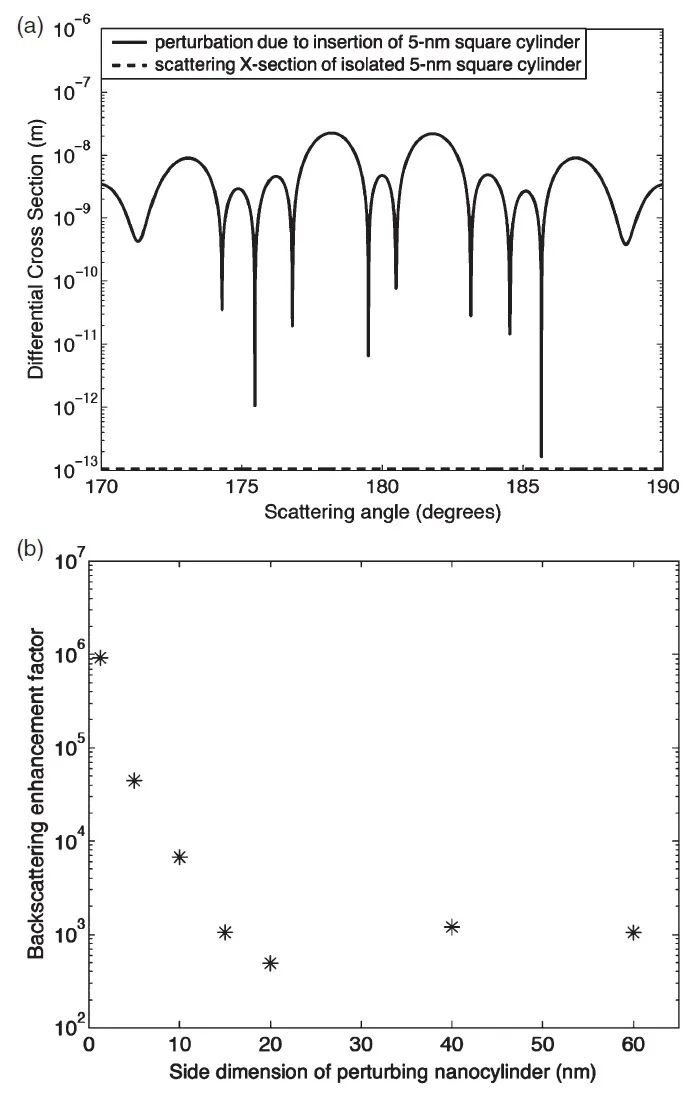
图3 (a) 在图2(b)的情况下(,,,),用FDTD计算的主介质圆柱的微分散射截面受到的扰动的绝对值。该扰动是将的方形介质纳米柱()放置在光子纳米喷射中心处的主微柱的表面上引起的。(b) 有效背向散射增强因子与扰动纳米柱截面尺寸的关系。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。
3. 介质球光子纳米喷射的最初确定
Li等人2最初确定了介质球产生的光子纳米喷射。他们的研究方法包括在球坐标系中求解麦克斯韦方程组的精确本征函数级数解(即米氏理论),用来计算被平面波照射的每个相关的介质球外部的近场。这种方式提供被平面波照射的微米级介质球可以产生最小束宽略小于衍射极限的全三维光子纳米喷射的证据。这种纳米喷射的特性与被平面波照射的尺寸以及与背景介质折射率的比值都相当的介质圆柱产生的二维纳米喷射相似。但是,相较于介质柱产生的纳米喷射,介质球产生的纳米喷射具有更高的强度。此外,当一纳米尺度的微粒放置于纳米喷射中时,介质球的背向散射功率比介质柱的背向散射功率所受到的扰动程度更大。
如图4所示,文献[2]首先研究了一系列折射率为的均匀、各向同性的介质微球。假设每个微球都在无限大的真空区域被沿方向偏振、沿向传播、波长为的单位强度的平面波照射。图4(a)、(b)、(c)、(d)分别显示了计算直径为、、和的每个微球得到的接近外部的场分布。当小于时(图4(a)~(c)),在微球的阴影面产生束腰略小于衍射极限的纳米喷射。当大于时(图4(d)),纳米喷射的强度峰值偏离微球表面。同时需要注意的是,纳米喷射的最大强度和FWHM束腰都随着的增加而增加。
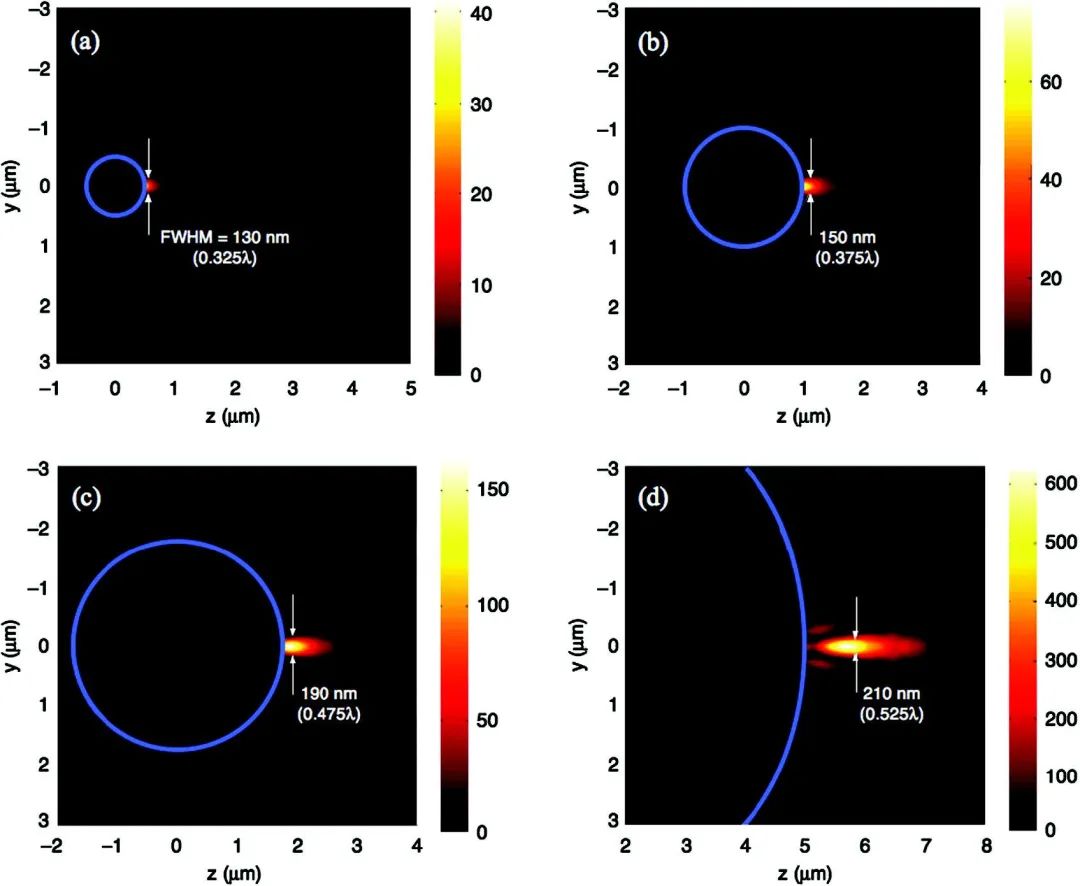
图4 显示了真空中折射率为的介质微球被波长为、方向偏振、沿向传播的单位强度的平面波照射所产生的光子纳米喷射。采用米氏级数计算近场。微球直径为:(a) ;(b) ;(c) ;(d) 。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

文献[2]接着研究了当一个直径为
、折射率为的金纳米粒子通过图4(c)所示的直径为的微球产生的纳米喷射时,微球的背向散射功率受到的扰动幅度。我们把由金纳米粒子造成的背向散射功率扰动的幅度峰值定义为。图5(a)按比例显示了所有微粒的尺度,说明了如何假定金纳米粒子在主微球阴影面外处的真空中沿方向的直线路径移动的。通过广义多粒子米氏方法(GMM)计算了微球/金纳米粒子的复合系统的背向散射,GMM方法基于矢量球谐波函数的叠加定理,24,25 能够给出多个球体的电磁波散射的严格解析解。
由图5(b)所示,相对于孤立微球的背向散射功率,沿图5(a)中所示路径移动的直径为的金纳米粒子产生的背向散射功率扰动的幅度峰值确定为。这相对来说是一个巨大的扰动,只比孤立微球的全部背向散射功率低,而且是由一个直径是微球直径的的纳米粒子引起的(也就是说,其截面面积比微球小多倍)。
由图5(c)所示,对直径到范围的金纳米粒子重复了上述研究。结果表明,随尺寸范围的增加而单调增加。事实上,对于这样小的金纳米粒子(直径大约为微球直径的),超过孤立微球背向散射功率的。有趣的是,一个直径的金纳米粒子,即由大约个金原子组成的团,产生的只比孤立微球的全部背向散射功率低。因此,动态范围为或以上的仪器可以使用可见光检测这种近原子级尺寸的粒子。
此外,图5(c)还揭示了当金纳米粒子的直径范围为(即)时,由它造成的背向散射功率的扰动按照增大。这比按照变化的瑞利散射慢得多。
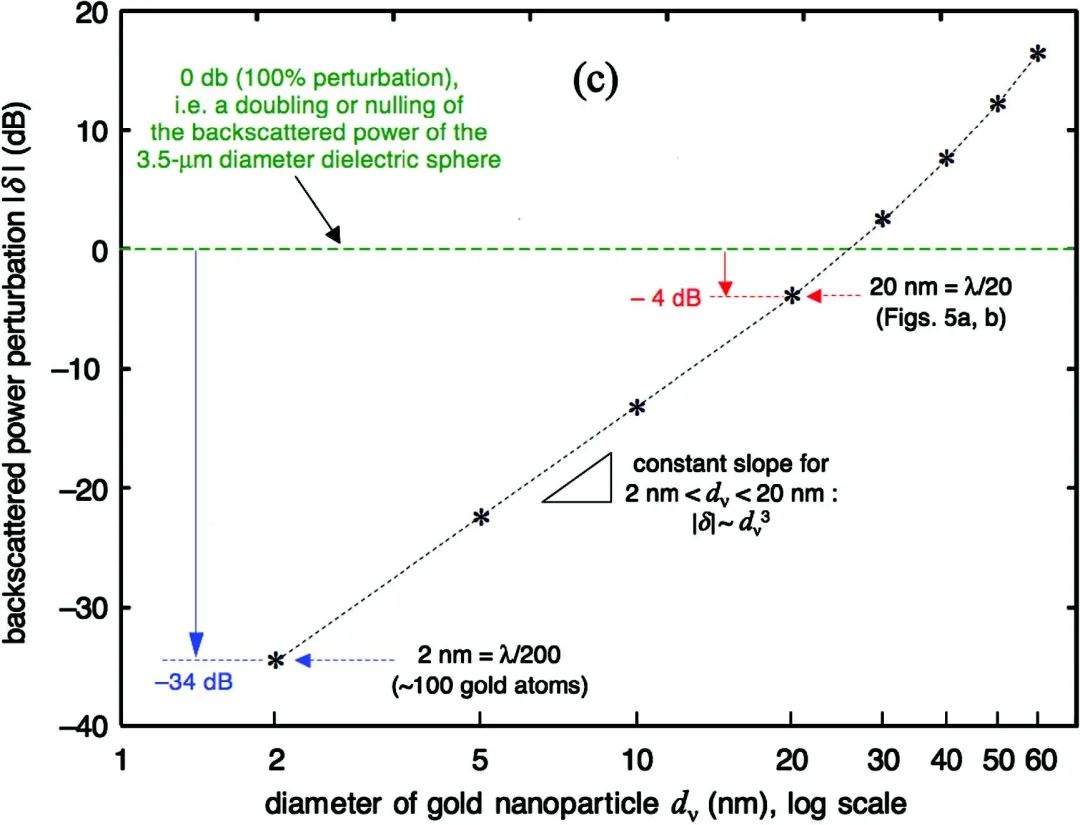
图5 (a) 一直径的金纳米粒子通过图4(c)的纳米喷射;(b) 对直径为的介质球的背向散射功率所产生的扰动;(c) 用表示的背向散射功率的扰动,相对于(a)中孤立的直径为的介质球的背向散射功率衡量。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

文献[2]继续计算了每个金纳米粒子直径下光子纳米喷射提供的有效背向散射增强因子。定义为由孤立的平面波照射的金纳米粒子的背向散射功率所归一化的值。参考图6(a)可以确定,当金纳米粒子的大小从降至时,从大约升高至。这两个值分别是图3(b)中所示的二维圆柱纳米喷射对应的增强因子的倍和倍。对于直径小于的纳米粒子,的增加呈现
的关系。结合在这个尺寸范围内大小相当可观的的值(图5(c)),有可能区分直径相差不到的金纳米粒子,如图6(b)所示。
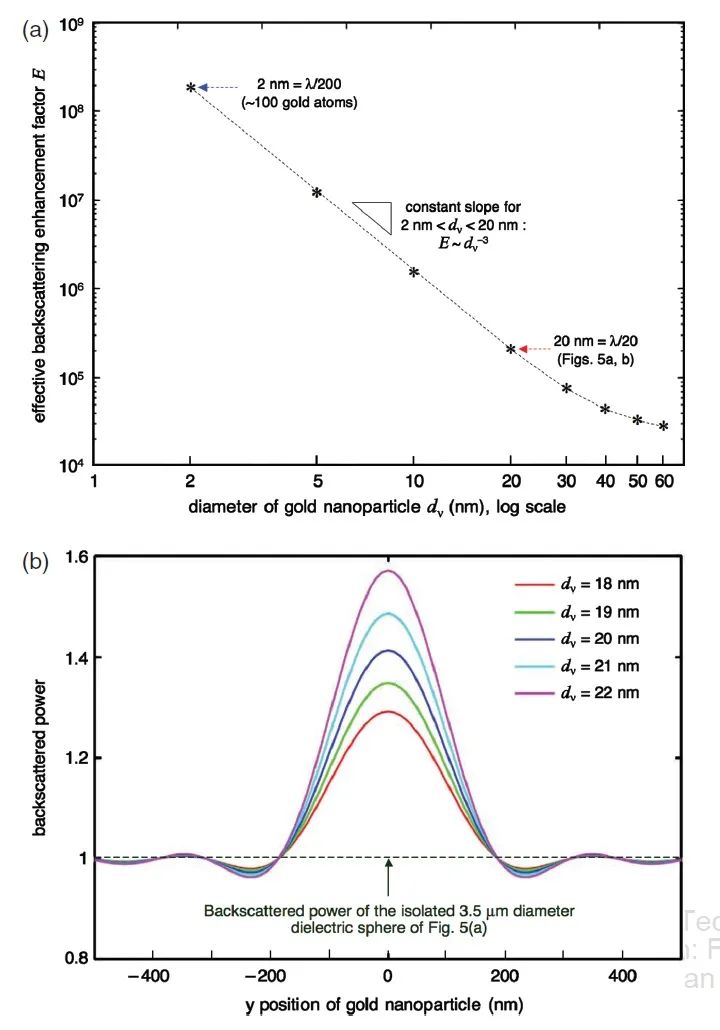
图6 (a) 起扰动作用的金纳米粒子的有效背向散射增强因子随其直径的变化;(b) 当金纳米粒子的直径从至变化时,微球/金纳米粒子系统背向散射功率变化的敏感性。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

4. 光子纳米喷射理论
Lecler等人3应用米氏理论分析了自由空间中平面波照射的介质微球产生的光子纳米喷射的一般三维矢量特性。他们报道称,当微球的直径在到超过的大范围内,都能够产生纳米喷射。他们进一步报道,纳米喷射的亚波长级束腰是微球的阴影面和它在外部空间的焦点(将微球看作透镜)接近的缘故。具体来说,对所考虑的微球,发现当微球有最佳折射率时,纳米喷射可以在最大约的传播距离内保持亚波长级的束腰。最后,纳米喷射和入射平面波表明有着同样的电场偏振,但具有不均匀的束宽(在入射磁场方向较窄)。
Itagi和Challener4对平面波照射的无限长介质圆柱的二维纳米喷射进行了细致的研究。他们的出发点是亥姆霍兹方程的本征函数解,它被写为德拜级数的形式(无限个向内和向外径向传播的圆柱波模式的求和,每个模式都可以在圆柱表面发生反射和透射)。结果表明,德拜级数的第一项特别重要。这一项得到一个紧凑的表达式,将纳米喷射的物理光学和几何光学性质结合起来,且允许简单的场分析。总的来说,结论是纳米喷射的特性是由角谱中的“独特特征组合”引起的,该角谱包含传播和倏逝空间频率的相位分布和有限成分。
在文献[2]中,Chen等人2报告了基于GMM理论对微球/纳米粒子系统进行的扰动分析,以检查和的变化关系的数学根源。他们指出,介质微球对入射光的透镜聚焦效应最多可以解释图6(a)中所示的八个数量级的背向散射增强因子中的三个数量级。此外,由于透镜聚焦效应在所考虑的范围内是恒定的,所以它对计算得到的和随的变化没有贡献。而和的变化关系的物理根源仍未得到解释。
Devilez等人20在严格的洛伦兹–米氏理论框架下研究了三维光子纳米喷射的空间和光谱特性。他们定量评估了包括传播波和倏逝波的所有空间频率分量的贡献。虽然他们的研究表明主要是传播波对纳米喷射有贡献,但被照射的微球产生的倏逝场分布增强和锐化了纳米喷射的场分布。这项分析的一个关键结论是,光子纳米喷射的角向开口至少小至相当的高斯光束的一半。

5. 实验观察
Heifetz等人6报道了实验研究,证实了此前文献[1]和[2]中预测的介质球的光子纳米喷射及相关的巨大的背向散射扰动现象。为了便于测量,原先报道的介质球直径从可见光照射的微米级尺寸向上放大到的微波()照射的厘米级尺寸。具体来说,介质球直径为(),由折射率为的丙烯酸材料(聚甲基丙烯酸甲酯)构成。
图7(a)描述了文献[6]中的测量数据,即由沿微波喷射的中心传播轴扫描得到的一直径为()的金属粒子所造成的背向散射扰动。这里,表示丙烯酸球的阴影面到金属粒子表面的距离。测量数据和用FDTD计算的数据很好地一致,它们表明在正值和负值之间振荡且取决于。扰动是“巨大的”,因为当其位于、和时,的金属粒子几乎可以将丙烯酸球的背向散射功率加倍;当其位于、和时,丙烯酸球的背向散射功率几乎被减半。尽管的金属粒子的直径仅为丙烯酸球的(即其面积仅为丙烯酸球的约)。
图7(b)显示的结果和图7(a)相似,在该图中,是在距丙烯酸球的阴影面()处采用的金属粒子沿电场方向横向扫过微波喷射。同样,其测量数据和用FDTD计算的数据具有很好的一致性。
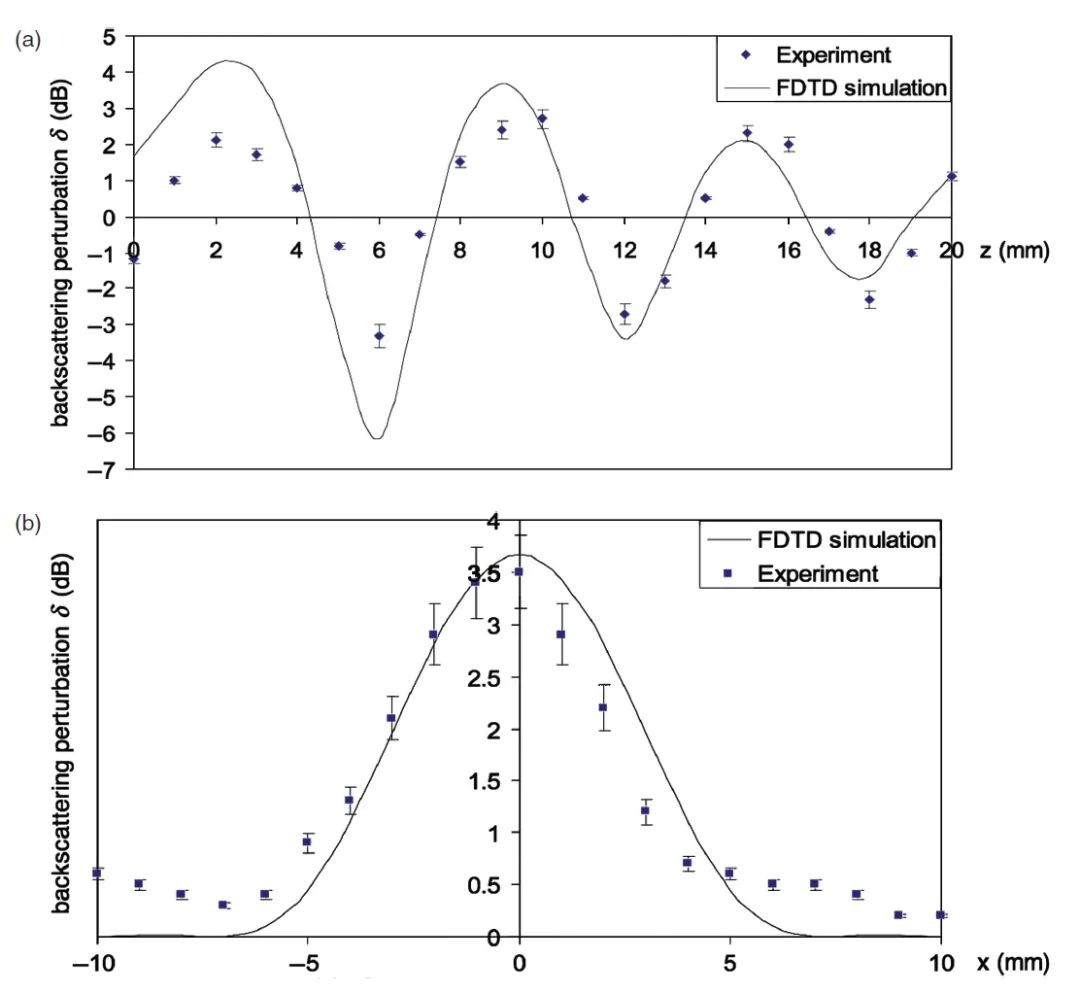
图7 (a) 由一直径为()的金属粒子沿()的微波喷射的中心传播轴扫描所造成的背向散射扰动的测量数据和FDTD模拟结果。是直径()的丙烯球的阴影面与金属粒子表面之间的距离;(b) 同(a)图,在此图中,的金属粒子在距丙烯酸球的阴影面 处沿电场方向横向扫过微波喷射。经文献[6]许可转载,A. Heifetz et al., Appl. Phys. Lett. 89, 221118 (2006)。

图8描述了文献[6]中背向散射功率的扰动随金属粒子直径
变化的测量数据,起扰动作用的金属粒子处于位置在 ()的微波喷射的中心传输轴上。这里,对测量数据进行拟合的直线的斜率给出了金属粒子直径处于(等效为)范围内的变化关系。这与图5(b)中绘制的使用GMM方法对直径(由于在图5(b)中假定入射光波长为,故等效为)的扰动金属粒子计算得到的理论关系相一致。
Ferrand等人13报告了在光波长下对光子纳米喷射的直接实验观测,如图9所示。这里,纳米喷射是由直径为、和的乳胶微球(折射率为)沉积于一玻璃盖片上并被波长的平面波照射而产生的。在检测模式下使用快速扫描共聚焦显微镜进行测量。每个全三维的光子纳米喷射都是从收集到的大量图像中重建得到的,这些图像已经通过数值反卷积过程进行了校正以考虑系统的检测点扩展函数的影响。测量结果显示,对于一个直径为的微球,其产生的纳米喷射的束宽可以小至FWHM为,并且纳米喷射可以在超过的传播距离上保持亚波长的FWHM束宽。

图8 测量得到的背向散射功率的扰动 ()随扰动金属粒子直径的变化关系,金属粒子处于位置在 ()的丙烯球阴影面后 ()处的 ()微波喷射的中心传输轴上。经文献[6]许可转载,A. Heifetz et al., Appl. Phys. Lett. 89, 221118 (2006)。


图9 (a) 显示了实验测量的位于玻璃盖片上的乳胶微球(折射率为)产生的光子纳米喷射,图从切过微球中心的垂直平面观察。入射光是一个向下传播的平面波,波长为。(b) 沿从纳米喷射最窄点切过的水平线上测量得到的经过单位峰值归一化后的强度值。红点:测量数据;实线:高斯曲线拟合。(c) 沿微球下方纳米喷射中心的垂直线上测量得到的经过入射波强度归一化后的强度值。蓝点:测量数据;实线:洛伦兹曲线拟合。(d) 纳米喷射的FWHM束宽与微球下方距离的关系。绿点:测量数据;虚线:假定微球处于自由空间的数值模拟结果。经文献[13]许可转载,P. Ferrand et al., Opt. Express 16, 6930 (2008)。

6 潜在应用
6.1 低损耗光波导
Astratov7,15报道了实验上观测到数十个平均直径在范围内相互接触的聚苯乙烯微球(折射率)构成的线性链中纳米喷射诱导模式 (NIMs) 的形成和传播的现象。在离源较远的位置,在直径为的微球构成的链内测量NIMs的传播损耗,每个微球的传播损耗低至。
由于NIMs不是共振模式而且具有固有的宽带性,所以通过微球链中NIMs传输的光波导可能比通过回音壁模式的球间耦合的光波导更有优势。通过NIMs,长链内微球直径受正常制造误差带来的变化对波导特性产生的影响就很小或接近于无了。

6.2 增强拉曼散射效应
Yi等人8报道了实验上观测到自组装的二氧化硅微球(直径,折射率)中的增强拉曼散射效应。他们的结论为,与二氧化硅微球相关的光子纳米喷射内部存在的强局域的光电场导致了拉曼散射效应的增强。
相较于传统的表面增强拉曼散射效应(SERS),微球增强的拉曼光谱更具有如下优势8:(1)介质球的位置和大小更好控制,避免了SERS的重复性问题;(2)样本制备要简单得多;(3)微球产生的增强效应可以在大多数拉曼活性基底中产生,如硅。这项技术在氧化、吸附、腐蚀和催化过程等表面科学领域有潜在的应用。

6.3 双光子荧光增强效应
Lecler等人9报道了实验上观测到通过添加几滴二氧化硅微球悬浮液(直径,折射率),分子染料溶液的双光子激发荧光的非线性增强的现象。他们认为非线性吸收是由与微球相关的光子纳米喷射而增强的,并认为光子纳米喷射可以用来增强其他非线性光学效应。

6.4 无掩模亚波长分辨率直写纳米图案
Wu等人10报道了一种无掩模亚波长分辨率的纳米图案直写技术的实验演示,该技术将一单层透明二氧化硅或聚苯乙烯微球(直径)的自组装平面阵列沉积在光刻胶的顶部。在短暂()的波长为的光照下,除了与微球相关的高强度光子纳米喷射的位置外,光刻胶没有被曝光。在一个大的光刻胶区域,这产生了一个规则的周期为、直径为的孔(或柱,如果使用负光刻胶处理)阵列。结果表明,通过改变曝光时间,该技术可以精确控制孔或柱的直径。此外,采用不同的微球粒径可以精确而独立地控制阵列周期。并且由于纳米喷射束腰只是微球直径的一个弱函数,即使微球尺寸的均匀性相对较差,也可以实现极均匀的孔或柱尺寸阵列。
McLeod和Arnold16报道了利用光学捕获的微球在聚酰亚胺薄膜衬底上直写复杂的纳米图案。这里,一个波长的连续激光器产生贝塞尔光束,用于光学捕获和操纵聚苯乙烯或二氧化硅微球。被捕获的微球同时被一波长的高斯脉冲光束照射以产生纳米喷射,从而局部修饰基底。当使用的聚苯乙烯微球时达到了最佳结果。以这种方式,他们演示了最小尺寸(不到直写波长的三分之一)的任意图案和单个形貌特征。在水和化学环境中定位精度优于,微球与衬底之间的间距保持在亚微米级,无需主动反馈控制。

6.5 纳米微粒检测、尺寸测量和定位
如第3节所述,使用GMM解析方法,文献[2]]首先报道了利用介质微球产生的光子纳米喷射的巨大背向散射扰动现象来检测和测量直径小于的金纳米球的可能性。随后,文献[11]采用GMM方法确定,当直径为的金纳米球放置在产生纳米喷射的介质微球后约的位置时,使用光子纳米喷射对其定位在磁场方向具有亚波长的横向空间分辨率,在背景介质中好至。尽管纳米粒子的直径仅为微球直径的,对金纳米粒子定位的背向散射扰动信号至多低于孤立微球背向散射的一个数量级。
综合起来,文献[2]和[11]表明,在几个波长分之一的相隔距离上,使用可见光以亚波长精度来检测、测量和定位小至几纳米的纳米粒子是可能的。一个潜在的生物光子学应用涉及到在水环境中检测附着在活细胞膜上的纳米粒子。在一个概念性实验中,可以通过一个光学捕获的微球产生的纳米喷射来扫描细胞,由于纳米喷射有软弹簧反冲作用,因而能最大限度减小对生物样品的潜在损害。

6.6 球形粒子对称聚集体中的定向发射
Gerlach等人12报道了光学方法测量相互接触的乳胶微球(折射率;直径 ,即)构成的小型对称阵列。在这里,微球之间的强光学耦合可导致其模式结构进行复杂的重新排布,类似于化学分子中的电子分子轨道。这种类比促成了“光子分子”一词12的使用。
他们测试了下列的紧凑分组情况:(a) 三个微球位于等边三角形的顶点;(b) 五个微球位于正五边形的顶点;(c) 七个微球,六个微球位于正六边形的顶点,包围着处于中心的第七个微球。每一组结构都是在硅片基底上形成的。在垂直于硅基底(即分子平面)的离焦激光束照射下,观察到光子纳米喷射从位于每组顶点的每个微球对称地向外传播。由于硅基底的反射,纳米喷射的发射在远场可见。
结论是,通过观察到的光子纳米喷射的定向发射,可以使用对称的微球组作为横向分束器,其输出端口数目等于位于用来排布微球所使用的等边三角形、五边形、六边形等顶点的微球数目。此外,这种光束分束方式可以允许从入射激光束到光子器件如沿平面基底排布的波导的横向耦合。这种耦合有可能达到亚波长的空间精度,且比传统的采用扫描近场光学显微镜尖端的亚波长耦合技术具有更高的强度。

6.7 半导体晶片的检查
Chen等人17申请了使用光子纳米喷射对半导体晶片进行光学测量的专利。在这种技术中,用纳米喷射扫描晶片的检查区域,并测量得到产生纳米喷射的介质微球的反射光。晶片表面形貌特征的存在、类型和尺寸是通过比较背向散射光的特征与所期望的结构和污染粒子的此类特征库来确定的。

6.8 金属纳米粒子的光学陷阱
Cui等人18从理论上研究了放置于由平面波照射介质微柱产生的光子纳米喷射中的金属纳米粒子受到的光学力。研究发现,这些光学力强烈地依赖于纳米粒子的介电常数和纳米喷射的强度与束宽。虽然亚波长金属纳米粒子可以有效地被捕获在纳米喷射中,但通过改变入射照明光的偏振,吸引力可变为排斥力。这种力的逆转与纳米粒子的极化率和局域表面等离激元的激发有关。总之,这些发现对于光子纳米喷射“提供高度束缚的力场以在纳米尺度上有效地组织纳米结构”的应用是非常有前景的。

6.9 超高密度数据存储光盘
Kong等人14,19计算和实验研究了光子纳米喷射在实现超高密度数据存储光盘方面的潜在应用,其中数据被编码为金属基底上的纳米凹陷。这个应用是基于之前报道的位于纳米喷射中孤立的纳米粒子所产生的巨大背向散射扰动的现象2,5,6 ;但在此处,是光盘基底的纳米凹陷(而不是孤立的纳米粒子)产生了背向散射的扰动。如图10所示,对尺寸放大的光盘模型的微波测量和FDTD计算模型表明,横向面积为平方波长的凹陷,即比目前的蓝光器件的特征尺寸还小得多,可以被稳健地检测到,其对比度比透镜系统高了约 14,26。这些发现,随后使用FDTD计算模拟扩展到光学波长19,表明光子纳米喷射可以促进比当前最前沿的技术具有更大容量和更高速度的光盘数据存储技术的发展。

图10 (a) 对于横向尺寸为 、深的矩形凹陷,纳米喷射导致的无凹陷和有凹陷的功率比随波长变化关系的实验和FDTD数据对比。这两个数据集都显示了无凹陷和有凹陷的峰值功率比相对于文献[25]报道的的数值大概提高了倍(即),文献[25]中是对以平方波长衡量的横向面积大约相同的八边形凹陷采用传统透镜得到的数据。(b) 显示了(a)图中凹陷的情况下采用FDTD计算的微波强度分布。在凹陷附近有一个很强的纳米喷射强度局域化分布,峰值为入射波的倍。其背向散射波强度随着距微球前表面的距离减小,且下降程度比没有凹陷时更快,形成一个弱得多的远场背向散射响应。经文献[14]许可转载,S.-C. Kong et al., Appl. Phys. Lett. 92, 211102 (2008)。

7 总结和结论
本文回顾了自2004年以来有关光子纳米喷射的大量文献。讨论内容包括对介质柱和介质球的光子纳米喷射的最初确定、光子纳米喷射的性质、纳米喷射理论、实验观察和潜在应用进行了综述。光子纳米喷射展现出理想特性的一种独特组合,包括沿多波长距离上路径的波传播(而不是倏逝波)、狭窄而潜在的亚波长束宽、高强度、波长灵敏度小以及纳米粒子和纳米凹陷引起的巨大背向散射扰动。因此,从超显微技术到光学数据存储、纳米图案化和生物光子学,光子纳米喷射对于推进当前纳米光子学技术具有相当大的前景。
Alexander Heifetz从伊利诺伊州埃文斯顿的西北大学于1999年获得应用数学学士学位(以优等成绩),2002年获得物理学硕士学位,2005年获得电子工程(光学)博士学位。他是西北大学Walter P. Murphy研究生奖学金的获得者。他博士论文的工作是全息光栅光衍射的信息存储和图像相关度的应用。他目前是美国癌症协会/金丝雀基金会的博士后研究员,在西北大学生物医学工程系工作。他的研究领域是生物医学应用的电磁散射理论与模拟。他最近的著作是关于利用米氏理论和时域有限差分法研究纳米粒子和生物细胞的光散射。
Soon-Cheol Kong分别于1995年、1997年和2003年从韩国首尔中央大学获得学士、硕士和博士学位。从2002年到2006年,他是韩国水原三星电子机械的高级研究员,从2004年到2005年,他是麻省理工学院的访问科学家。目前,他在西北大学担任博士后研究员。他的研究领域包括时域有限差分法、微波光子学、微/纳电磁学、天线在生物光子学中的应用、行波光电探测器、超高密度光存储、太阳能电池、生物检测和癌症早期检测。
Alan V. Sahakian从威斯康星大学麦迪逊分校获得了电子工程硕士学位、电子和计算机工程专业博士学位并辅修计算机科学。在研究生期间,他也是Medtronic公司的高级电气工程师。他在威斯康星大学帕克赛德分校获得了应用科学和物理学的学士学位。他目前是西北大学EECS和BME专业的教授和EECS大学本科课程项目的副主席。他也是EECS信号和系统部门主任和埃文斯顿医院学术机构的成员。他曾是空军技术学院可靠性和可维护性卓越中心的常驻访问学者。他是IEEE的会士。除了心电生理学,他的实验室还研究微波、毫米波和光子学方法的医学成像和诊断。他的研究由NSF(国家科学基金会)、国防部乳腺癌研究计划、国防情报局、爽健(Dr. Scholl)基金会和Medtronic公司资助。
Allen Taflove是美国伊利诺伊州埃文斯顿西北大学电子工程和计算机科学教授,自1971年以来,他一直帮助开创时域有限差分法(FDTD)的算法和应用。他的著作包括超过125篇期刊论文和《计算电动力学:时域有限差分法》的三个版本(1995年、2000年和2005年),该书已成为FDTD领域的标准参考书。他被科学信息研究所列为世界上被引用最多的技术作者之一。
Vadim Backman是西北大学McCormick工程与应用科学学院生物医学工程教授。他从哈佛大学和麻省理工学院获得了医学工程博士学位。他获得了许多荣誉,包括被《技术评论》杂志评选为全球前100名青年创新者之一和国家科学基金会职业奖。Backman博士的研究领域包括开发用于疾病的非侵入式筛查、诊断和检测的新颖生物光子学技术。研究的重点是纳米尺度、微观尺度和分子水平。
Z. G. Chen, A. Taflove, and V. Backman, Opt. Express 12, 1214 (2004).
X. Li, Z. Chen, A. Taflove, and V. Backman, Opt. Express 13, 526 (2005).
S. Lecler, Y. Takakura, and P. Meyrueis, Optics Lett. 30, 2641 (2005).
A. V. Itagi and W. A. Challener, J. Opt. Soc. America A 22, 2847 (2005).
Z. G. Chen, X. Li, A. Taflove, and V. Backman, Optics Lett. 31, 196 (2006).
A. Heifetz, K. Huang, A. V. Sahakian, X. Li, A. Taflove, and V. Backman, Appl. Phys. Lett. 89, 221118 (2006).
A. M. Kapitonov and V. N. Astratov, Optics Lett. 32, 409 (2007).
K. J. Yi, H. Wang, Y. F. Lu, and Z. Y. Yang, J. Applied Physics 101, 063528 (2007).
S. Lecler, S. Haacke, N. Lecong, O. Crégut, J.-L. Rehspringer, and C. Hirlimann, Opt. Express 15, 4935 (2007).
W. Wu, A. Katsnelson, O. G. Memis, and H. Mohseni, Nanotechnology 18, 485302 (2007).
A. Heifetz, J. J. Simpson, S.-C. Kong, A. Taflove, and V. Backman, Opt. Express 15, 17334 (2007).
M. Gerlach, Y. P. Rakovich, and J. F. Donegan, Opt. Express 15, 17343 (2007).
P. Ferrand, J. Wenger, A. Devilez, M. Pianta, B. Stout, N. Bonod, E. Popov, and H. Rigneault, Opt. Express 16, 6930 (2008).
S.-C. Kong, A. V. Sahakian, A. Heifetz, A. Taflove, and V. Backman, Appl. Phys. Lett. 92, 211102 (2008).
S. Yang and V. N. Astratov, Appl. Phys. Lett. 92, 261111 (2008).
E. McLeod and C. B. Arnold, Nature Nanotech. 3, 413 (2008).
Z. Chen, H. Chu, and S. Li, Optical metrology using a photonic nanojet, U.S. Patent 7,394,535 (2008).
X. Cui, D. Erni, and C. Hafner, Opt. Express 16, 13560 (2008).
S.-C. Kong, A. Sahakian, A. Taflove, and V. Backman, Opt. Express 16, 13713 (2008).
A. Devilez, B. Stout, N. Bonod, and E. Popov, Opt. Express 16, 14200 (2008).
A. Taflove and S. C. Hagness, Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd edn., Artech, Boston (2005).
C. L. Adler, J. A. Lock, B. R. Stone, and C. J. Garcia, J. Opt. Soc. America A 14, 1305 (1997).
J. A. Lock, C. L. Adler, and E. A. Hovenac, J. Opt. Soc. America A 17, 1846 (2000).
Y. L. Xu and R. T. Wang, Phys. Rev. E 58, 3931 (1998).
Online: http://www.astro.ufl.edu/∼xu/.
J. A. C. Veerman, A. J. H. Wachters, A. M. van der Lee, and H. P. Urbach, Opt. Express 15, 2075 (2007).
B. S. Luk’yanchuk, R. Paniagua-Domínguez, I. Minin, O. Minin and Z. Wang, Refractive index less than two: photonic nanojets yesterday, today and tomorrow, Optical Materials Express, 7(6):1820-1847, 2017 https://doi.org/10.1364/OME.7.001820I.
V. Minin, C.-Y. Liu, Y. E. Geints and O. V. Minin, Recent advances in integrated photonic jet-based photonics, Photonics, 7(2):41, 2020 http://dx.doi.org/10.3390/photonics7020041
A. J. Littlefield, J. Zhu, J. F. Messinger and L. L. Goddard, Photonic nanojets, Optics & Photonics News, 32(1):34–41, 2021 http://dx.doi.org/10.1364/OPN.32.1.00003
A. Darafsheh, Photonic nanojets and their applications, Journal of Physics: Photonics, 3(2):022001, 2021 https://doi.org/10.1088/2515-7647/abdb05


推荐两本FDTD的教材以纪念上月底去世的FDTD牛人 Allen Taflove教授。




光学前沿—驾驭太赫兹空隙
本文译自Sidney Perkowitz所撰写的Navigating the terahertz gap一文,文章发表在Physics World, 2020, 33(3):37–40上。翻译目的为分享知识,欢迎指正。如有侵权,请告知删除。点击文末原文链接可以阅读英文原文。




仔细去看一张教室里的海报,上面展示了从伽马射线到无线电波整个广阔的电磁频谱,你会发现处于红外和微波之间的一小块区域。它被称为远红外、亚毫米或太赫兹波,名义上被定义为从中红外波段的到微波波段的的波长范围。尽管在这些教育海报中并不突出,但这个波长范围是地球上和地球外物理学的丰富研究领域。

[图片来自其他网站,翻译者添加]

虽然有微波和红外光源可以在那些频率下产生数千瓦的功率,但缺乏在太赫兹频率范围工作良好的光源,这就是为什么它常常被称为“太赫兹间隙”。热的黑体在太赫兹频率下只产生微瓦的功率,而微波技术不容易被推广到毫米波长以下,因此标准的光谱方法不适用。然而,这一频率间隙非常值得开拓。它是探测凝聚态物质的电子、晶格和量子性质以及研究大分子的合适频率范围。它可以应用于生物医学、安检系统和艺术品研究。在实验室外,太赫兹辐射与宇宙微波背景辐射 (CMB)和其他天体物理现象有关,有助于寻找太空生命的起源。
1. 用微瓦和毫瓦功率将就
幸运的是,当科学家们看到理解上存在空白时,他们马上投入研究。自20世纪60年代以来,研究人员已经找到了利用傅里叶变换光谱仪获得高质量太赫兹光谱的方法。在这个装置中,一个热源向固体、液体或气体样品发送微瓦的太赫兹功率,被样品反射或透射。接下来,光束被分成两部分,每部分被镜子反射。然后光束被重新组合,当一面镜子相对另一面镜子移动时,探测器测量产生的干涉信号。通过对这个干涉图的傅里叶分析得到样品的特定频谱,其信噪比高于传统光谱仪。
另一种制造太赫兹辐射源且可以得到更高功率的常用方法是用CO2激光对有机分子介质(如甲醇CH3OH)的振动态进行光学泵浦。这会激发分子的转动亚能级,发射出离散的太赫兹激光谱线。不同的介质以毫瓦的功率提供数百条谱线,从而在很宽的范围内得到精确的数据。
自20世纪60年代和70年代以来,在我的实验室和其他实验室,这种太赫兹傅里叶光谱仪和泵浦激光器已经用来探测半导体及其纳米结构、超导体、非均匀材料、液态和气态水以及生物分子。但最近,基于半导体技术(见2016年6月期第28-31页)和同步加速器和自由电子激光器(见第40页方框)的强且新的太赫兹源提升了实验室的研究。事实上,根据澳大利亚卧龙岗大学Roger Lewis在2014年进行的一项文献计量研究,1975年至2013年间,发表的摘要、标题或关键词中包含“太赫兹”的论文数量呈指数增长(J. Phys. D: Appl. Phys. 47 374001)。

2. 太赫兹物理学升空
早在1964年,太赫兹物理学也受到了强大的推动以走出实验室进入宇宙。就在那时,阿诺·彭齐亚斯(Arno Penzias)和罗伯特·威尔逊(Robert Wilson)在贝尔实验室使用为卫星通信设计的天线工作,意外地发现了一个微波波长为7.35 cm的恒定信号,它似乎均匀地分布在天空中。
对这种未知辐射的决定性测量是在1989年发射的美国宇航局(NASA)宇宙背景探测器 (COBE)卫星上进行的。使用傅里叶变换光谱仪,COBE的结果与黑体在2.725±0.002 K下的发射曲线几乎完全一致。该光谱的峰值强度位于1.07 mm,跨越了太赫兹范围(图1),而彭齐亚斯和威尔逊抓住了曲线的末端。另外,COBE还比较了来自不同天空方向的毫米波辐射,发现CMB具有轻微的各向异性,代表了105分之一的温度波动(见2020年2月期第36–40页)。

这些黑体数据与1965年宇宙学家罗Robert Dicke、Philip Peebles及其同事的预测相符,即随着在大爆炸后冷却,宇宙将充满~3 K的剩余黑体辐射。数据的一致性为大爆炸理论提供了有力的支持,其结果对宇宙历史提供了深刻的见解。事实上,当乔治·斯穆特(George Smoot)和约翰·马瑟(John Mather)因为在COBE方面的工作而获得2006年诺贝尔物理学奖时,诺贝尔委员会指出COBE可以“被视为宇宙学作为一门精确科学的起点”。
CMB的温度波动也很显著;它们代表了宇宙大爆炸38万年后组成宇宙的氢的密度变化。它们演化成今天的宇宙结构,星系的细丝被巨大的空洞包围。COBE之后,NASA于2001年发射的威尔金森微波各向异性探测器(WMAP)和欧洲航天局(European Space Agency)于2009年发射的普朗克号(Planck)飞船从太空研究了这种波动。探测方法和空间技术的进步改进了随后的各项任务。普朗克号飞船用热探测器探测到微弱的信号,探测器冷却到0.1 K并发出阿瓦特量级的噪声,在9个频率处覆盖了从0.03 THz (10 mm)到0.857 THz (0.35 mm)间最宽的频率范围。飞船测量到的宇宙温差为5 µK或更小,角分辨率低至4 角分,相比之下,COBE的值为7°,WMAP为0.5°(图2)。
利用所谓的“含宇宙常数的冷暗物质模型”(ΛCDM)(宇宙“标准模型”)对普朗克号的太赫兹辐射数据进行了分析。ΛCDM假设物理学,包括广义相对论,在整个宇宙中都是相同的;宇宙最初是热的、稠密的,并且一直在膨胀;宇宙包括暗能量、暗物质、普通物质、光子和中微子。2018年,普朗克号的最终结果显示,宇宙有138亿年的历史;它包含31.5%的物质(4.9%的普通物质和26.6%的暗物质)和68.5%的暗能量;它很可能只包含三种中微子,它们的质量总和小于0.12 eV;宇宙正在膨胀,哈勃常数H0为67.4 km/s/Mpc。
这些结果为我们提供了迄今为止最准确和最全面的宇宙图像,其中太赫兹探测技术发挥了重要作用。然而,由于不确定度仅为1%,普朗克号的H0值与根据其他据信可靠的天体物理数据得出的值73 km/s/Mpc存在差异—这种差异可能指向新的物理学。

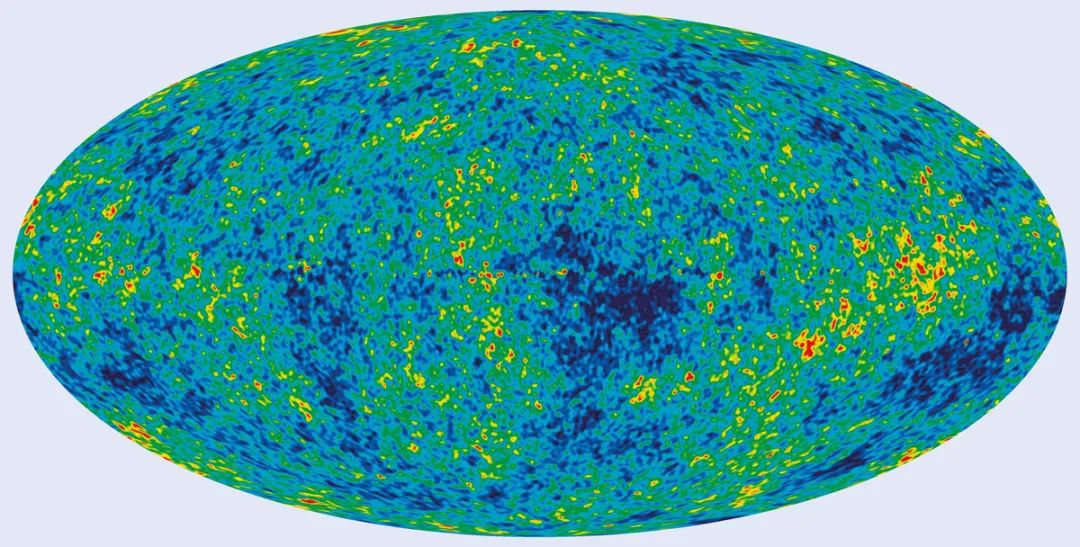

图2 COBE、WMAP和普朗克号飞船在太赫兹范围内对早期宇宙温度变化的分辨率逐渐提高的观测。


3. 采用毫米波观测黑洞
另一个太赫兹天体物理工程要求的分辨率远远高于普朗克号达到的分辨率。2019年4月,国际事件视界望远镜 (Event Horizon Telescope, EHT)合作展示了有史以来第一张黑洞图像—位于5500万光年外的椭圆星系M87中心的超大质量黑洞(见2019年5月期第8-10页)。
该工程的目的是通过观察黑洞的“阴影”来研究视界附近的区域,这是一个由流入黑洞的热吸积物质发出的微光中的黑暗区域。这个阴影是由视界附近引力弯曲并捕获光线造成的,其直径约为广义相对论预测的施瓦西半径(黑洞半径)的五倍。它只张开约40微弧秒的一个小角度。
太赫兹光子描绘了一个黑洞,因为它们来自黑洞引力阱的深处。在波长1.3 mm到7 mm之间对M87的早期研究显示了一个中心40微弧秒结构的迹象,但无法对其进行成像。然而,这些结果确实表明,毫米波长越短,光子就能更准确地描绘黑洞在明亮区域内的实际位置。但是没有一个单独的单天线或多天线射电望远镜装置能够在毫米波长提供所需的角分辨率。
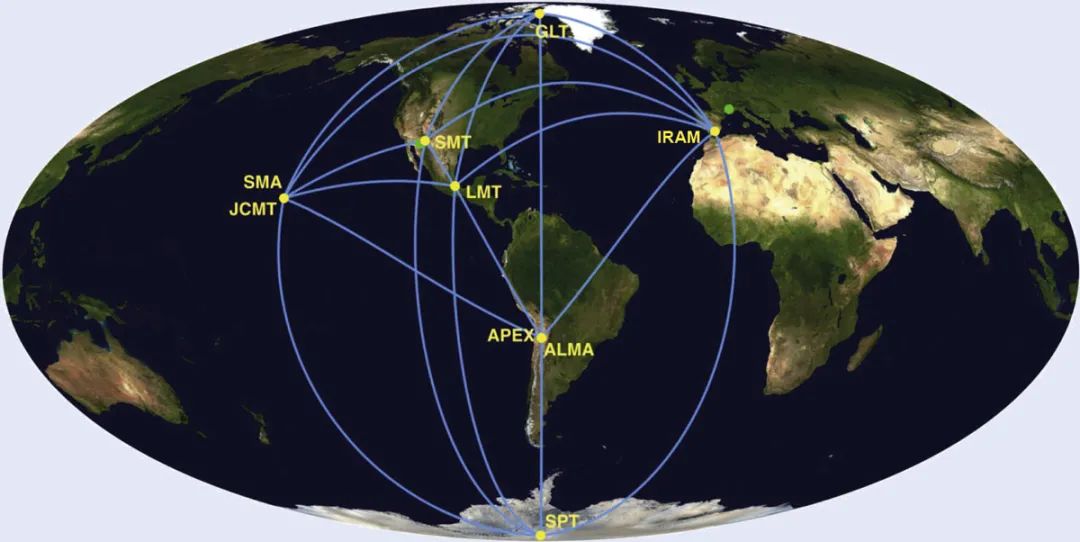
解决方案是EHT将地球周围的8个独立装置连接起来,包括智利沙漠中的阿塔卡玛毫米/亚毫米波阵列望远镜 (Atacama Large Millimeter/submillimeter Array, ALMA)、南极洲的南极望远镜(South Pole Telescope, SPT)和西班牙的IRAM 30米望远镜(图3)。由此得到的虚拟望远镜给出了1.3 mm波长除以地球直径这个量级的角分辨率。经过协调望远镜和分析PB字节数据的复杂过程后,合成网络产生了分辨率为20 微弧秒的引人注目的图像。它清楚地显示了42 微弧秒宽的明亮辐射区内的暗影,暗影本身显示了细节。对数据的分析给出了一个6.5×109倍太阳质量的中心质量,决定性地确立了M87中存在一个超大质量黑洞的证据,并支持了这种大小的黑洞位于星系中心的假设。

在太赫兹频段以航天器为基础的的天体物理学和宇宙学研究—例如测量宇宙微波背景的波动—之所以成为可能,是因为像COBE和Planck这样的项目中灵敏的探测器经过低温冷却以降低噪声。在实验室中,灵敏的探测器对于使用来自微瓦级热源的太赫兹傅里叶变换光谱技术也很重要。
太赫兹光谱技术的另一种途径是开发更强的光源。光学泵浦的激光器(见正文)产生毫瓦级功率,这对于许多用途来说是足够的,但它们需要一个二氧化碳激光器,而且不像黑体,不能覆盖连续的频率范围。其他强太赫兹源也有不同的限制。量子级联激光器(QCL,见2016年6月期第28–31页)是一种半导体纳米结构,可产生更高的功率,但频率固定,需要低温冷却。最近的一篇论文(L H Li et al. 2017 Electronics Letters 53 799)描述了一种QCL,冷却至77 K和10 K时在4.4 THz处分别输出1.8 W和2.4 W。
中央设施能够提供更高功率来满足如太赫兹显微术等高功率需求的应用。一种光源在自由电子激光器中产生强太赫兹波,其中一相对论电子束经过一组磁极交替分布的磁铁。这使电子产生横向摆动运动,从而产生单色光子,其频率可通过改变电子速度或磁场来调节,并将其束缚在腔中而变得相干。例如,加州大学圣巴巴拉分校的自由电子激光器在0.1 THz到4.8 THz范围输出千瓦的功率。位于俄罗斯新西伯利亚的布德克核物理研究所(Budker Institute of Nuclear Physics)的另一个装置工作在1.2至8.2 THz。

新光源 纽约布鲁克海文国家实验室的NCLS-II装置具有产生太赫兹波的能力。
高功率太赫兹辐射也可以由同步加速器储存环中循环的电子产生。纽约布鲁克海文国家实验室的国家同步加速器光源(National Synchrotron Light Source)保持运行着一条THz束线,在0.15 THz以上的宽带范围提供100 mW的功率,覆盖太赫兹及以上的范围,并作为傅里叶变换光谱仪的光源。另一个同步加速器的束线是位于萨斯喀彻温省的萨斯喀彻温大学的加拿大光源(Canadian Light Source),作为傅里叶变换光谱技术和太赫兹显微技术的光源,它也以高亮度覆盖了太赫兹频率范围。
通过对探测器、光源或两者的明智选择,科学家们已经在太赫兹空隙找到了立足点并进行了最高质量的研究。但理想的太赫兹辐射源—产生毫瓦或更搞的功率,可在整个范围内调谐,紧凑且在室温下工作—仍然是难以达到的。这是安检系统和生物医学应用的一个主要障碍。

4. 寻找生命的分子
除了在太空探索宇宙起源和发展的研究外,太赫兹方法还可以研究一系列不同的基础问题。地球上的生命是如何开始的?这是一个独特的过程,意味着我们在宇宙中是孤独的吗?还是在别的地方孕育了生命?
这些大问题的一个可能答案是,生命的复杂分子或其前体起源于星际物质,并通过陨石来到地球和其他行星。根据我们对地球生命的了解,这意味着要在太空中找到含有碳以及氢、氧和氮的有机分子。其中一些分子—包括构建蛋白质所必需的氨基酸—已经在降落到地球上的陨石中发现,现在太赫兹天文光谱正被用来在太空中寻找这些生命的或生命起源前的分子。
宇宙似乎支持以活性碳为基础的化学过程—事实上,在太空中发现的第一个分子是1937年发现的CH,从那时起通过紫外到厘米波长的光谱发现的200多种分子中有机分子仍然占主导。这些结果大多来自频率低于2 THz的射电天文学,在这个范围,与分子转动相关的能级之间的跃迁提供了许多可识别的发射或吸收光谱特征。这与实验室中用甲醇 CH3OH(也在太空中被发现)等化合物产生太赫兹激光谱线的机理相同。
已知的天文有机分子包含多达13个原子(不包括非生命的富勒烯C60和C70),这是一个与生物功能相关的复杂度。据报道,2003年在太空中发现了简单的氨基酸甘氨酸(NH2CH2COOH),但后来的测量没有证实这一点。其他相关发现包括与糖相关的分子乙醇醛(CH2OHCHO)和甲酰胺(NH2CHO),后者是一种可能的生命前体,具有形成糖和氨基酸的合适性质。
类似ALMA这样的望远镜阵列提供的高角分辨率有助于寻找空间中大多数大有机分子中发现的直链碳骨架以外的复杂性。2014年,德国波恩的马克斯普朗克射电天文学研究所Arnaud Belloche领导的一个团队利用3 mm波长的ALMA发现了第一个具有支链碳链的太空分子异丙基氰化物(iso-propyl cyanide, i-C3H7CN)。这是在地球上的陨石中发现的氨基酸的典型特征。在我们银河系巨大的星体形成气体云人马座(Sagittarius)B2中观察到了这种分子,这表明太空中的活跃区域倾向于制造复杂的化合物。更深入的对分子是如何在不同的地方—从星际(interstellar)和星周(circumstellar)区域到原行星盘(protoplanetary disc)—形成的物理和化学层面的理解,将进一步集中寻找生物分子的工作。
复杂分子光谱的实验室测量对于指导天文研究和解释其结果是必不可少的。例如,Susanna Widicus Weave是埃默里大学(Emory University)的化学家,她致力于改进太赫兹傅里叶变换光谱和其他方法,以达到上述目的并研究星际化学的新领域,例如与冰的分子反应。她在最近的一篇综述论文 (Ann. Rev. Astron. Astrophys. 57 79)写道,这些技术“有望填补太赫兹空隙…提供的分析技术可与电磁频谱中的微波和红外波段相匹敌”。
研究人员已经在地球上和地球外扩展了微波和红外方法,以使太赫兹空隙可以驾驭,并在这两个波段进行了创新性研究。这种广度说明了太赫兹科学的跨学科性质,因为它探索了宇宙的起源、太空和地球上物质的性质,以及非生命分子跃进变为生命的迷人而神秘的交叉点。



中英双语