光学前沿—光子纳米喷射

本文译自Alexander Heifetz等所撰写的Photonic Nanojets一文,文章发表在Journal of Computational and Theoretical Nanoscience, 2009, 6(9):1979–1992上。此文为本科毕业设计任务所翻译题目,目的为分享知识,欢迎指正。如有侵权,请告知删除。点击文末原文链接可以阅读英文原文。


本文回顾了自2004年以来有关光子纳米喷射的主要文献。光子纳米喷射是从被照射的直径大于波长的无损介质微柱或微球的阴影面后出射的狭窄、高强度的光束,它是一种非倏逝波并可以传播超过波长的距离。纳米喷射的最小束宽可以小于经典衍射极限,对于微球来说,实际上束宽可以小至。当其折射率与背景折射率之比小于约2:1时,在微柱或微球大范围的直径范围内会出现光子纳米喷射这种非共振现象。重要的是,在纳米喷射中放置直径为
的纳米粒子会使被光照射的微球的远场背向散射功率受到扰动,在固定波长下其扰动量随变化。对于同一孤立的纳米粒子,这种扰动比按照变化的瑞利散射要慢得多。这导致了这样一种情况,例如,如果将直径为的纳米粒子放入到由直径为的微球产生的纳米喷射中,尽管纳米粒子的截面面积仅为微球的万分之一,测量到的微球远场散射功率可以达到原先的两倍。实际上,纳米喷射的作用是将纳米粒子的存在投射到远场。这些特性结合在一起,使得光子纳米喷射在检测和操纵纳米量级的物体、超衍射分辨率纳米图案成形和纳米光刻、低损耗波导和超高密度光学存储等方面具有潜在的重要应用价值。

1. 引言
自2004年以来,出现了大量关于光子纳米喷射的存在、性质和潜在应用的大量文献1–20。光子纳米喷射是从被平面波照射的直径大于入射波长的无损介质微柱或微球的阴影面后向背景介质中传播的狭窄、高强度的电磁波。光子纳米喷射的主要特性包括:(1)它是一种非倏逝的传播波,在介质柱或球外延伸超过的路径上其半高全宽(FWHM)的横向光束宽度可保持在亚波长。(2)它的最小FWHM束宽可以小于经典衍射极限,对于微球来说,实际上束宽可以小至。(3)当介质折射率与背景折射率之比小于约时,在微柱或微球的直径处于到的大范围内会出现光子纳米喷射这种非共振现象。(4)它的强度很高,大大超过入射光强度。(5)在纳米喷射中放置直径为的纳米粒子会使被光照射的微球的远场背向散射功率受到扰动,在固定波长下其扰动量随变化。对于同一孤立的纳米粒子,这种扰动比按照变化的瑞利散射要慢得多。这导致了这样一种情况,例如,如果将直径为的纳米粒子放入到由直径为的微球产生的纳米喷射中,尽管纳米粒子的截面面积仅为微球的万分之一,测量到的微球远场散射功率可以达到原先的两倍。实际上,纳米喷射的作用是将纳米粒子的存在投射到远场。这些特性结合在一起,使得光子纳米喷射在检测和操纵纳米量级的物体、超衍射分辨率纳米图案成形和纳米光刻、低损耗波导和超高密度光学存储等方面具有潜在的重要应用价值。本文综述了迄今为止纳米喷射领域的研究进展,旨在推动纳米喷射方面的研究。本文讨论的内容包括:介质柱光子纳米喷射的最初确定(第2节);介质球光子纳米喷射的最初确定(第3节);光子纳米喷射理论(第4节);实验观察(第5节);以及潜在的应用(第6节)。
2. 介质柱光子纳米喷射的最初确定
Chen等人1最初将光子纳米喷射确定为一种独特的电磁波类型,并创造“光子纳米喷射”这个术语来描述它。利用高分辨率的时域有限差分算法(FDTD)求解麦克斯韦方程组,21 证明当一平面波照射微米尺度的介质圆柱时,会产生一个狭窄、高强度、束宽低于衍射极限的光束,从微柱的阴影面向背景介质中传播。报告进一步指出,当在纳米喷射内放置一纳米尺度的介质圆柱时,产生纳米喷射的微米尺度介质柱的背向散射功率会受到巨大的扰动。也就是说,扰动比孤立的纳米圆柱的背向散射大几个数量级。
文献[1]首先回顾了FDTD算法的验证,采用了大小为的均匀方形网格(在所有模拟运算中比波长的还要精细)和网格外围的完美匹配层吸收边界条件。21 通过将用FDTD计算的几种均匀、各向同性的介质圆柱的微分散射截面和精确级数解作比较,发现在的动态范围内研究的所有情况下,整个散射角范围内误差在 以内。
文献[1]接着报道了对一列均匀、各向同性、无损、无限长的介质圆柱的内部和近外部场的详细的二维计算研究。假定每一个圆柱都被入射电场与圆柱无限长轴平行的平面波照射。图1显示的示例结果说明了光子纳米喷射随介质圆柱折射率减小的演化过程。这里显示了FDTD计算的正弦稳态电场的包络,所研究的结构为放置在折射率的无限真空介质中的直径为、均匀折射率为的圆柱。波长为的光在介质2中从左向右传播。当从图1(a)中的降至图1(b)中的时,圆柱内部电场峰值向阴影面移动。进一步把降至图1(c)中的时,电场峰值从圆柱的阴影面出现,呈强喷射状分布,长度为,FWHM强度束腰为略低于衍射极限的 。这种从的圆柱阴影面出现的喷射和以前关于光学焦散的研究工作是一致的。22, 23

图1 光子纳米喷射随被平面波照射的介质圆柱折射率减小发生的演化过程的演示。显示了FDTD计算的正弦稳态电场的包络,所研究的结构为放置在折射率的无限真空介质中的直径为、均匀折射率为的圆柱。波长为的光在介质2中从左向右传播。(a) ;(b) ;(c) 。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。

文献[1]接着报道,如果的值相较于图1(c)中的值不发生显著变化,那么类似于图1(c)中的束腰略小于衍射极限的光子纳米喷射可以通过、、和的不同组合来产生。图2给出了多个例子:(a) ,,,;(b) ,,,;(c) ,,,。包括图1(c)的情况,所有模拟的纳米喷射的FWHM强度束腰范围在到之间,长度在到之间。
最后,通过FDTD模拟,文献[1]考虑了将起扰动作用的纳米级介质柱置于微米级主柱产生的纳米喷射中带来的影响。测试使用了图2(b)中的参数,即一个直径为、折射率为的主圆柱放置在折射率为的无限外部介质中,照射光波长为。假设扰动纳米介质柱具有边长为的方形截面,且其折射率为。在FDTD模型中,该纳米柱被放入直径为的主柱表面的光子纳米喷射的中心。
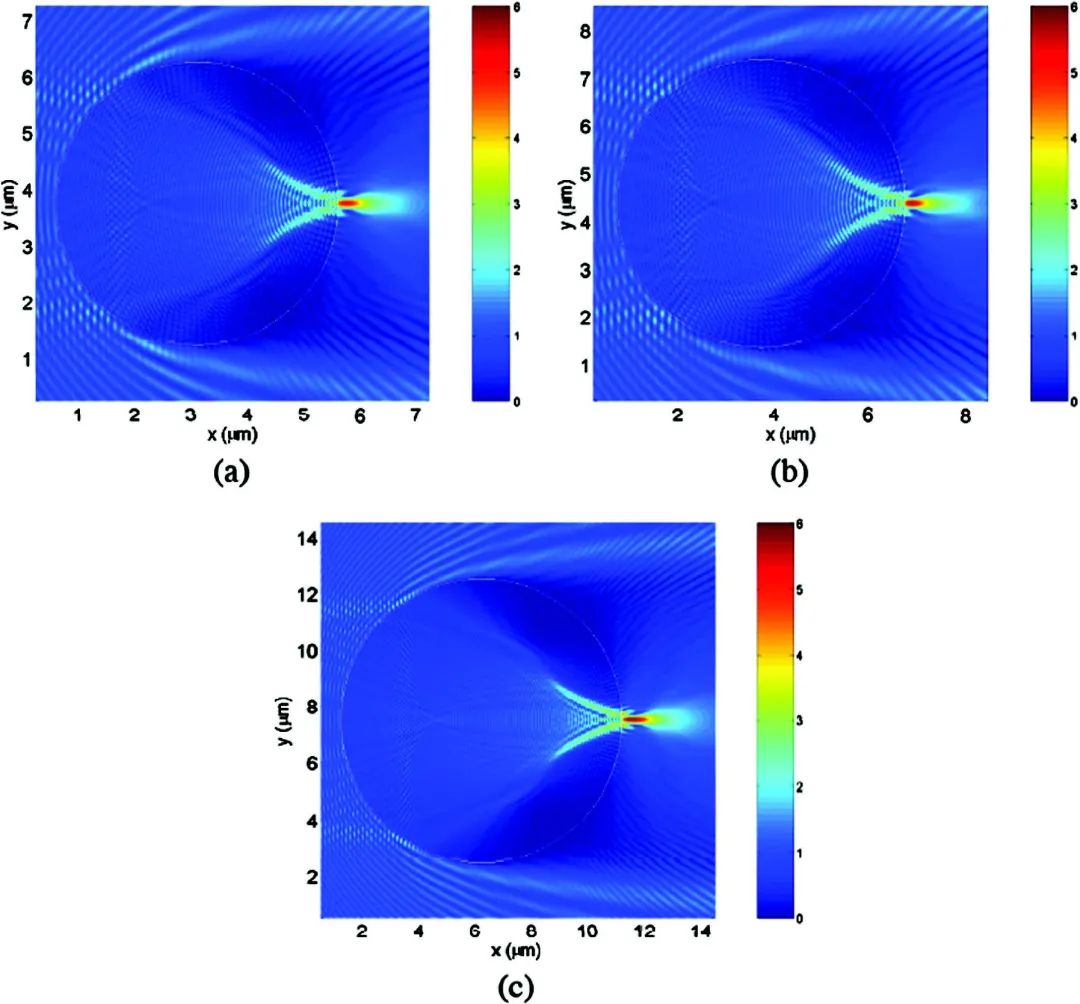
图2 与图1(c)中类似的、、和三种不同组合所产生的光子纳米喷射的演示。(a) ,,,;(b) ,,,;(c) ,,,。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。

图3(a)绘制了在背向散射范围内主微柱的微分散射截面受到的扰动的绝对值。此图还绘制了对应的被平面波照射的孤立扰动纳米柱的微分散射截面。这些结果表明,位于纳米喷射中的的介质纳米柱对微柱的直接背向散射截面的扰动大约是孤立纳米柱背向散射的倍。图3(b)给出了文献[1]中额外的FDTD模拟结果,表明当
减小到以下时,扰动纳米柱背向散射的有效增强(用表示)单调增加,且当时达到大约的水平。
基于以上计算模拟的结果,文献[1]总结到,光子纳米喷射可能会提供一种检测尺寸远低于经典衍射极限的纳米粒子的新方法。这有潜力为如下应用提供新的手段:使用可见光检测蛋白质、病毒粒子甚至单个分子;监测在生物学、化学、材料科学和组织工程许多领域具有重要意义的分子合成和聚集过程。
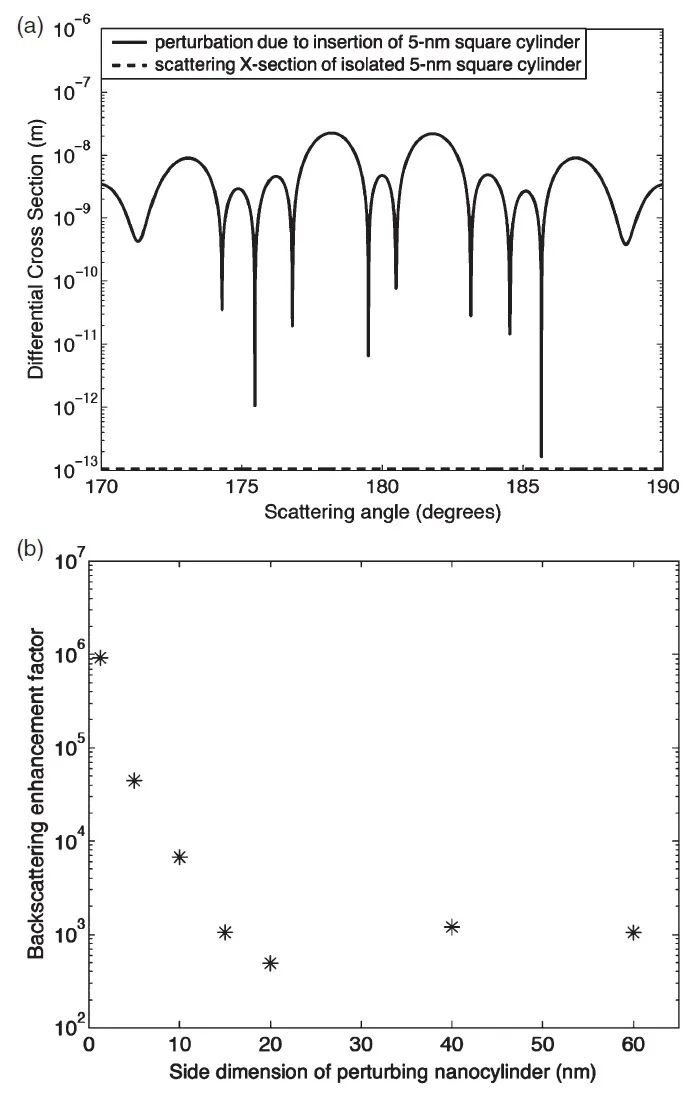
图3 (a) 在图2(b)的情况下(,,,),用FDTD计算的主介质圆柱的微分散射截面受到的扰动的绝对值。该扰动是将的方形介质纳米柱()放置在光子纳米喷射中心处的主微柱的表面上引起的。(b) 有效背向散射增强因子与扰动纳米柱截面尺寸的关系。经文献[1]许可转载,Z. G. Chen et al., Opt. Express 12, 1214 (2004)。
3. 介质球光子纳米喷射的最初确定
Li等人2最初确定了介质球产生的光子纳米喷射。他们的研究方法包括在球坐标系中求解麦克斯韦方程组的精确本征函数级数解(即米氏理论),用来计算被平面波照射的每个相关的介质球外部的近场。这种方式提供被平面波照射的微米级介质球可以产生最小束宽略小于衍射极限的全三维光子纳米喷射的证据。这种纳米喷射的特性与被平面波照射的尺寸以及与背景介质折射率的比值都相当的介质圆柱产生的二维纳米喷射相似。但是,相较于介质柱产生的纳米喷射,介质球产生的纳米喷射具有更高的强度。此外,当一纳米尺度的微粒放置于纳米喷射中时,介质球的背向散射功率比介质柱的背向散射功率所受到的扰动程度更大。
如图4所示,文献[2]首先研究了一系列折射率为的均匀、各向同性的介质微球。假设每个微球都在无限大的真空区域被沿方向偏振、沿向传播、波长为的单位强度的平面波照射。图4(a)、(b)、(c)、(d)分别显示了计算直径为、、和的每个微球得到的接近外部的场分布。当小于时(图4(a)~(c)),在微球的阴影面产生束腰略小于衍射极限的纳米喷射。当大于时(图4(d)),纳米喷射的强度峰值偏离微球表面。同时需要注意的是,纳米喷射的最大强度和FWHM束腰都随着的增加而增加。
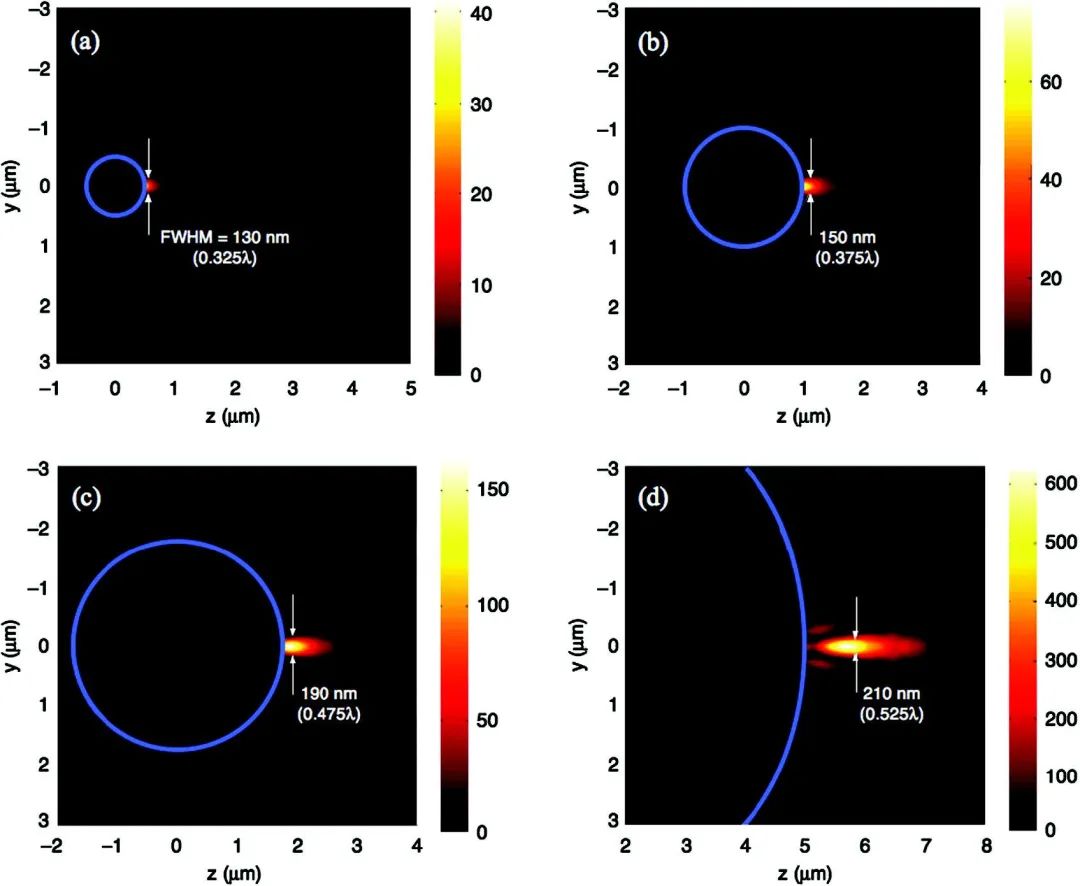
图4 显示了真空中折射率为的介质微球被波长为、方向偏振、沿向传播的单位强度的平面波照射所产生的光子纳米喷射。采用米氏级数计算近场。微球直径为:(a) ;(b) ;(c) ;(d) 。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

文献[2]接着研究了当一个直径为
、折射率为的金纳米粒子通过图4(c)所示的直径为的微球产生的纳米喷射时,微球的背向散射功率受到的扰动幅度。我们把由金纳米粒子造成的背向散射功率扰动的幅度峰值定义为。图5(a)按比例显示了所有微粒的尺度,说明了如何假定金纳米粒子在主微球阴影面外处的真空中沿方向的直线路径移动的。通过广义多粒子米氏方法(GMM)计算了微球/金纳米粒子的复合系统的背向散射,GMM方法基于矢量球谐波函数的叠加定理,24,25 能够给出多个球体的电磁波散射的严格解析解。
由图5(b)所示,相对于孤立微球的背向散射功率,沿图5(a)中所示路径移动的直径为的金纳米粒子产生的背向散射功率扰动的幅度峰值确定为。这相对来说是一个巨大的扰动,只比孤立微球的全部背向散射功率低,而且是由一个直径是微球直径的的纳米粒子引起的(也就是说,其截面面积比微球小多倍)。
由图5(c)所示,对直径到范围的金纳米粒子重复了上述研究。结果表明,随尺寸范围的增加而单调增加。事实上,对于这样小的金纳米粒子(直径大约为微球直径的),超过孤立微球背向散射功率的。有趣的是,一个直径的金纳米粒子,即由大约个金原子组成的团,产生的只比孤立微球的全部背向散射功率低。因此,动态范围为或以上的仪器可以使用可见光检测这种近原子级尺寸的粒子。
此外,图5(c)还揭示了当金纳米粒子的直径范围为(即)时,由它造成的背向散射功率的扰动按照增大。这比按照变化的瑞利散射慢得多。
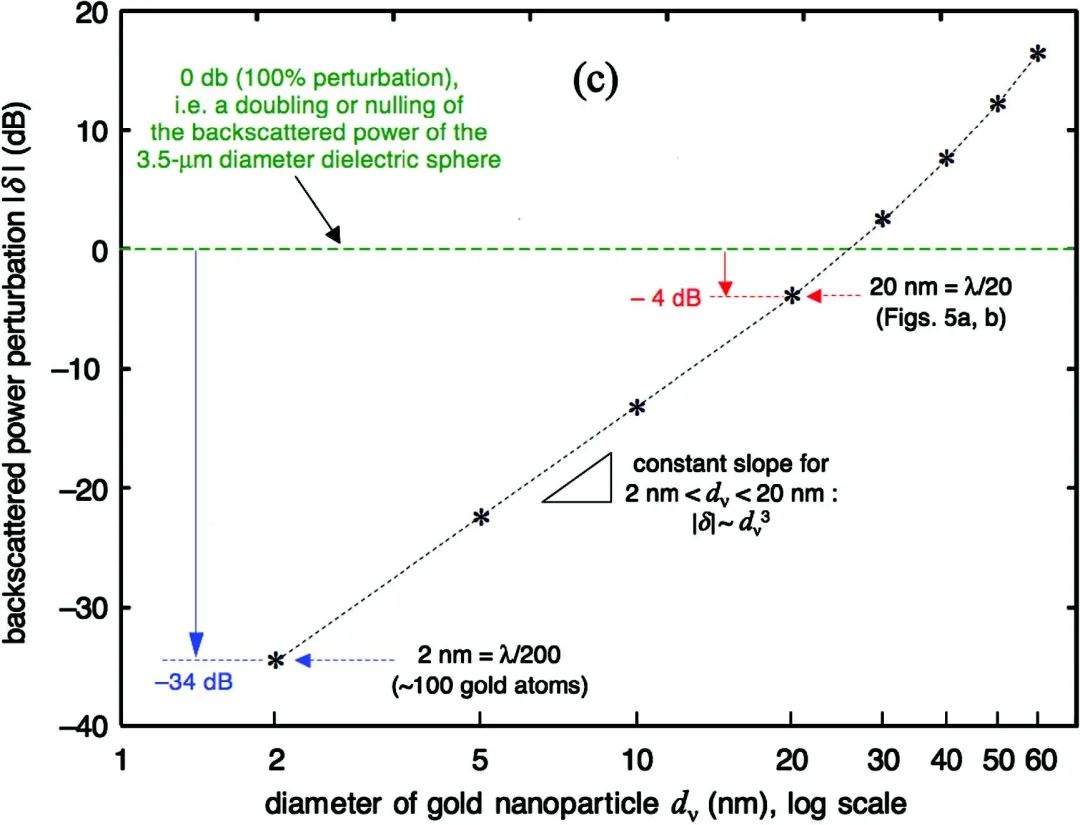
图5 (a) 一直径的金纳米粒子通过图4(c)的纳米喷射;(b) 对直径为的介质球的背向散射功率所产生的扰动;(c) 用表示的背向散射功率的扰动,相对于(a)中孤立的直径为的介质球的背向散射功率衡量。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

文献[2]继续计算了每个金纳米粒子直径下光子纳米喷射提供的有效背向散射增强因子。定义为由孤立的平面波照射的金纳米粒子的背向散射功率所归一化的值。参考图6(a)可以确定,当金纳米粒子的大小从降至时,从大约升高至。这两个值分别是图3(b)中所示的二维圆柱纳米喷射对应的增强因子的倍和倍。对于直径小于的纳米粒子,的增加呈现
的关系。结合在这个尺寸范围内大小相当可观的的值(图5(c)),有可能区分直径相差不到的金纳米粒子,如图6(b)所示。
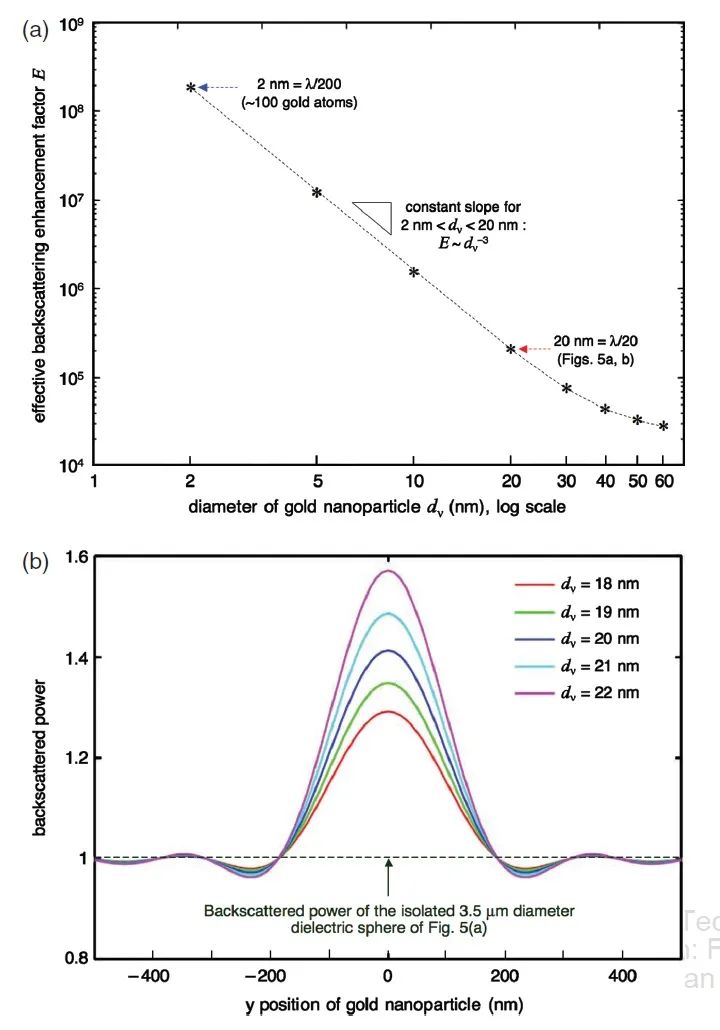
图6 (a) 起扰动作用的金纳米粒子的有效背向散射增强因子随其直径的变化;(b) 当金纳米粒子的直径从至变化时,微球/金纳米粒子系统背向散射功率变化的敏感性。经文献[2]许可转载,X. Li et al., Opt. Express 13, 526 (2005)。

4. 光子纳米喷射理论
Lecler等人3应用米氏理论分析了自由空间中平面波照射的介质微球产生的光子纳米喷射的一般三维矢量特性。他们报道称,当微球的直径在到超过的大范围内,都能够产生纳米喷射。他们进一步报道,纳米喷射的亚波长级束腰是微球的阴影面和它在外部空间的焦点(将微球看作透镜)接近的缘故。具体来说,对所考虑的微球,发现当微球有最佳折射率时,纳米喷射可以在最大约的传播距离内保持亚波长级的束腰。最后,纳米喷射和入射平面波表明有着同样的电场偏振,但具有不均匀的束宽(在入射磁场方向较窄)。
Itagi和Challener4对平面波照射的无限长介质圆柱的二维纳米喷射进行了细致的研究。他们的出发点是亥姆霍兹方程的本征函数解,它被写为德拜级数的形式(无限个向内和向外径向传播的圆柱波模式的求和,每个模式都可以在圆柱表面发生反射和透射)。结果表明,德拜级数的第一项特别重要。这一项得到一个紧凑的表达式,将纳米喷射的物理光学和几何光学性质结合起来,且允许简单的场分析。总的来说,结论是纳米喷射的特性是由角谱中的“独特特征组合”引起的,该角谱包含传播和倏逝空间频率的相位分布和有限成分。
在文献[2]中,Chen等人2报告了基于GMM理论对微球/纳米粒子系统进行的扰动分析,以检查和的变化关系的数学根源。他们指出,介质微球对入射光的透镜聚焦效应最多可以解释图6(a)中所示的八个数量级的背向散射增强因子中的三个数量级。此外,由于透镜聚焦效应在所考虑的范围内是恒定的,所以它对计算得到的和随的变化没有贡献。而和的变化关系的物理根源仍未得到解释。
Devilez等人20在严格的洛伦兹–米氏理论框架下研究了三维光子纳米喷射的空间和光谱特性。他们定量评估了包括传播波和倏逝波的所有空间频率分量的贡献。虽然他们的研究表明主要是传播波对纳米喷射有贡献,但被照射的微球产生的倏逝场分布增强和锐化了纳米喷射的场分布。这项分析的一个关键结论是,光子纳米喷射的角向开口至少小至相当的高斯光束的一半。

5. 实验观察
Heifetz等人6报道了实验研究,证实了此前文献[1]和[2]中预测的介质球的光子纳米喷射及相关的巨大的背向散射扰动现象。为了便于测量,原先报道的介质球直径从可见光照射的微米级尺寸向上放大到的微波()照射的厘米级尺寸。具体来说,介质球直径为(),由折射率为的丙烯酸材料(聚甲基丙烯酸甲酯)构成。
图7(a)描述了文献[6]中的测量数据,即由沿微波喷射的中心传播轴扫描得到的一直径为()的金属粒子所造成的背向散射扰动。这里,表示丙烯酸球的阴影面到金属粒子表面的距离。测量数据和用FDTD计算的数据很好地一致,它们表明在正值和负值之间振荡且取决于。扰动是“巨大的”,因为当其位于、和时,的金属粒子几乎可以将丙烯酸球的背向散射功率加倍;当其位于、和时,丙烯酸球的背向散射功率几乎被减半。尽管的金属粒子的直径仅为丙烯酸球的(即其面积仅为丙烯酸球的约)。
图7(b)显示的结果和图7(a)相似,在该图中,是在距丙烯酸球的阴影面()处采用的金属粒子沿电场方向横向扫过微波喷射。同样,其测量数据和用FDTD计算的数据具有很好的一致性。
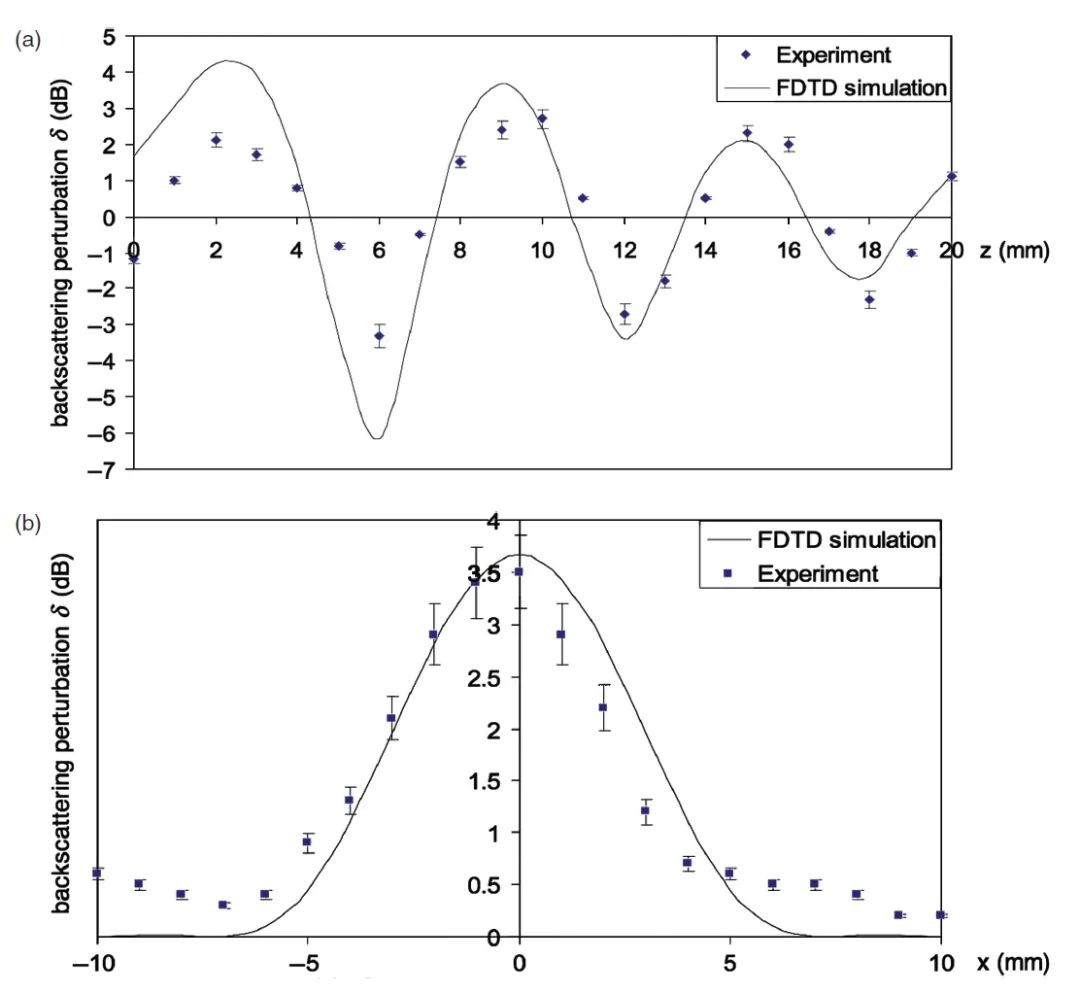
图7 (a) 由一直径为()的金属粒子沿()的微波喷射的中心传播轴扫描所造成的背向散射扰动的测量数据和FDTD模拟结果。是直径()的丙烯球的阴影面与金属粒子表面之间的距离;(b) 同(a)图,在此图中,的金属粒子在距丙烯酸球的阴影面 处沿电场方向横向扫过微波喷射。经文献[6]许可转载,A. Heifetz et al., Appl. Phys. Lett. 89, 221118 (2006)。

图8描述了文献[6]中背向散射功率的扰动随金属粒子直径
变化的测量数据,起扰动作用的金属粒子处于位置在 ()的微波喷射的中心传输轴上。这里,对测量数据进行拟合的直线的斜率给出了金属粒子直径处于(等效为)范围内的变化关系。这与图5(b)中绘制的使用GMM方法对直径(由于在图5(b)中假定入射光波长为,故等效为)的扰动金属粒子计算得到的理论关系相一致。
Ferrand等人13报告了在光波长下对光子纳米喷射的直接实验观测,如图9所示。这里,纳米喷射是由直径为、和的乳胶微球(折射率为)沉积于一玻璃盖片上并被波长的平面波照射而产生的。在检测模式下使用快速扫描共聚焦显微镜进行测量。每个全三维的光子纳米喷射都是从收集到的大量图像中重建得到的,这些图像已经通过数值反卷积过程进行了校正以考虑系统的检测点扩展函数的影响。测量结果显示,对于一个直径为的微球,其产生的纳米喷射的束宽可以小至FWHM为,并且纳米喷射可以在超过的传播距离上保持亚波长的FWHM束宽。

图8 测量得到的背向散射功率的扰动 ()随扰动金属粒子直径的变化关系,金属粒子处于位置在 ()的丙烯球阴影面后 ()处的 ()微波喷射的中心传输轴上。经文献[6]许可转载,A. Heifetz et al., Appl. Phys. Lett. 89, 221118 (2006)。


图9 (a) 显示了实验测量的位于玻璃盖片上的乳胶微球(折射率为)产生的光子纳米喷射,图从切过微球中心的垂直平面观察。入射光是一个向下传播的平面波,波长为。(b) 沿从纳米喷射最窄点切过的水平线上测量得到的经过单位峰值归一化后的强度值。红点:测量数据;实线:高斯曲线拟合。(c) 沿微球下方纳米喷射中心的垂直线上测量得到的经过入射波强度归一化后的强度值。蓝点:测量数据;实线:洛伦兹曲线拟合。(d) 纳米喷射的FWHM束宽与微球下方距离的关系。绿点:测量数据;虚线:假定微球处于自由空间的数值模拟结果。经文献[13]许可转载,P. Ferrand et al., Opt. Express 16, 6930 (2008)。

6 潜在应用
6.1 低损耗光波导
Astratov7,15报道了实验上观测到数十个平均直径在范围内相互接触的聚苯乙烯微球(折射率)构成的线性链中纳米喷射诱导模式 (NIMs) 的形成和传播的现象。在离源较远的位置,在直径为的微球构成的链内测量NIMs的传播损耗,每个微球的传播损耗低至。
由于NIMs不是共振模式而且具有固有的宽带性,所以通过微球链中NIMs传输的光波导可能比通过回音壁模式的球间耦合的光波导更有优势。通过NIMs,长链内微球直径受正常制造误差带来的变化对波导特性产生的影响就很小或接近于无了。

6.2 增强拉曼散射效应
Yi等人8报道了实验上观测到自组装的二氧化硅微球(直径,折射率)中的增强拉曼散射效应。他们的结论为,与二氧化硅微球相关的光子纳米喷射内部存在的强局域的光电场导致了拉曼散射效应的增强。
相较于传统的表面增强拉曼散射效应(SERS),微球增强的拉曼光谱更具有如下优势8:(1)介质球的位置和大小更好控制,避免了SERS的重复性问题;(2)样本制备要简单得多;(3)微球产生的增强效应可以在大多数拉曼活性基底中产生,如硅。这项技术在氧化、吸附、腐蚀和催化过程等表面科学领域有潜在的应用。

6.3 双光子荧光增强效应
Lecler等人9报道了实验上观测到通过添加几滴二氧化硅微球悬浮液(直径,折射率),分子染料溶液的双光子激发荧光的非线性增强的现象。他们认为非线性吸收是由与微球相关的光子纳米喷射而增强的,并认为光子纳米喷射可以用来增强其他非线性光学效应。

6.4 无掩模亚波长分辨率直写纳米图案
Wu等人10报道了一种无掩模亚波长分辨率的纳米图案直写技术的实验演示,该技术将一单层透明二氧化硅或聚苯乙烯微球(直径)的自组装平面阵列沉积在光刻胶的顶部。在短暂()的波长为的光照下,除了与微球相关的高强度光子纳米喷射的位置外,光刻胶没有被曝光。在一个大的光刻胶区域,这产生了一个规则的周期为、直径为的孔(或柱,如果使用负光刻胶处理)阵列。结果表明,通过改变曝光时间,该技术可以精确控制孔或柱的直径。此外,采用不同的微球粒径可以精确而独立地控制阵列周期。并且由于纳米喷射束腰只是微球直径的一个弱函数,即使微球尺寸的均匀性相对较差,也可以实现极均匀的孔或柱尺寸阵列。
McLeod和Arnold16报道了利用光学捕获的微球在聚酰亚胺薄膜衬底上直写复杂的纳米图案。这里,一个波长的连续激光器产生贝塞尔光束,用于光学捕获和操纵聚苯乙烯或二氧化硅微球。被捕获的微球同时被一波长的高斯脉冲光束照射以产生纳米喷射,从而局部修饰基底。当使用的聚苯乙烯微球时达到了最佳结果。以这种方式,他们演示了最小尺寸(不到直写波长的三分之一)的任意图案和单个形貌特征。在水和化学环境中定位精度优于,微球与衬底之间的间距保持在亚微米级,无需主动反馈控制。

6.5 纳米微粒检测、尺寸测量和定位
如第3节所述,使用GMM解析方法,文献[2]]首先报道了利用介质微球产生的光子纳米喷射的巨大背向散射扰动现象来检测和测量直径小于的金纳米球的可能性。随后,文献[11]采用GMM方法确定,当直径为的金纳米球放置在产生纳米喷射的介质微球后约的位置时,使用光子纳米喷射对其定位在磁场方向具有亚波长的横向空间分辨率,在背景介质中好至。尽管纳米粒子的直径仅为微球直径的,对金纳米粒子定位的背向散射扰动信号至多低于孤立微球背向散射的一个数量级。
综合起来,文献[2]和[11]表明,在几个波长分之一的相隔距离上,使用可见光以亚波长精度来检测、测量和定位小至几纳米的纳米粒子是可能的。一个潜在的生物光子学应用涉及到在水环境中检测附着在活细胞膜上的纳米粒子。在一个概念性实验中,可以通过一个光学捕获的微球产生的纳米喷射来扫描细胞,由于纳米喷射有软弹簧反冲作用,因而能最大限度减小对生物样品的潜在损害。

6.6 球形粒子对称聚集体中的定向发射
Gerlach等人12报道了光学方法测量相互接触的乳胶微球(折射率;直径 ,即)构成的小型对称阵列。在这里,微球之间的强光学耦合可导致其模式结构进行复杂的重新排布,类似于化学分子中的电子分子轨道。这种类比促成了“光子分子”一词12的使用。
他们测试了下列的紧凑分组情况:(a) 三个微球位于等边三角形的顶点;(b) 五个微球位于正五边形的顶点;(c) 七个微球,六个微球位于正六边形的顶点,包围着处于中心的第七个微球。每一组结构都是在硅片基底上形成的。在垂直于硅基底(即分子平面)的离焦激光束照射下,观察到光子纳米喷射从位于每组顶点的每个微球对称地向外传播。由于硅基底的反射,纳米喷射的发射在远场可见。
结论是,通过观察到的光子纳米喷射的定向发射,可以使用对称的微球组作为横向分束器,其输出端口数目等于位于用来排布微球所使用的等边三角形、五边形、六边形等顶点的微球数目。此外,这种光束分束方式可以允许从入射激光束到光子器件如沿平面基底排布的波导的横向耦合。这种耦合有可能达到亚波长的空间精度,且比传统的采用扫描近场光学显微镜尖端的亚波长耦合技术具有更高的强度。

6.7 半导体晶片的检查
Chen等人17申请了使用光子纳米喷射对半导体晶片进行光学测量的专利。在这种技术中,用纳米喷射扫描晶片的检查区域,并测量得到产生纳米喷射的介质微球的反射光。晶片表面形貌特征的存在、类型和尺寸是通过比较背向散射光的特征与所期望的结构和污染粒子的此类特征库来确定的。

6.8 金属纳米粒子的光学陷阱
Cui等人18从理论上研究了放置于由平面波照射介质微柱产生的光子纳米喷射中的金属纳米粒子受到的光学力。研究发现,这些光学力强烈地依赖于纳米粒子的介电常数和纳米喷射的强度与束宽。虽然亚波长金属纳米粒子可以有效地被捕获在纳米喷射中,但通过改变入射照明光的偏振,吸引力可变为排斥力。这种力的逆转与纳米粒子的极化率和局域表面等离激元的激发有关。总之,这些发现对于光子纳米喷射“提供高度束缚的力场以在纳米尺度上有效地组织纳米结构”的应用是非常有前景的。

6.9 超高密度数据存储光盘
Kong等人14,19计算和实验研究了光子纳米喷射在实现超高密度数据存储光盘方面的潜在应用,其中数据被编码为金属基底上的纳米凹陷。这个应用是基于之前报道的位于纳米喷射中孤立的纳米粒子所产生的巨大背向散射扰动的现象2,5,6 ;但在此处,是光盘基底的纳米凹陷(而不是孤立的纳米粒子)产生了背向散射的扰动。如图10所示,对尺寸放大的光盘模型的微波测量和FDTD计算模型表明,横向面积为平方波长的凹陷,即比目前的蓝光器件的特征尺寸还小得多,可以被稳健地检测到,其对比度比透镜系统高了约 14,26。这些发现,随后使用FDTD计算模拟扩展到光学波长19,表明光子纳米喷射可以促进比当前最前沿的技术具有更大容量和更高速度的光盘数据存储技术的发展。

图10 (a) 对于横向尺寸为 、深的矩形凹陷,纳米喷射导致的无凹陷和有凹陷的功率比随波长变化关系的实验和FDTD数据对比。这两个数据集都显示了无凹陷和有凹陷的峰值功率比相对于文献[25]报道的的数值大概提高了倍(即),文献[25]中是对以平方波长衡量的横向面积大约相同的八边形凹陷采用传统透镜得到的数据。(b) 显示了(a)图中凹陷的情况下采用FDTD计算的微波强度分布。在凹陷附近有一个很强的纳米喷射强度局域化分布,峰值为入射波的倍。其背向散射波强度随着距微球前表面的距离减小,且下降程度比没有凹陷时更快,形成一个弱得多的远场背向散射响应。经文献[14]许可转载,S.-C. Kong et al., Appl. Phys. Lett. 92, 211102 (2008)。

7 总结和结论
本文回顾了自2004年以来有关光子纳米喷射的大量文献。讨论内容包括对介质柱和介质球的光子纳米喷射的最初确定、光子纳米喷射的性质、纳米喷射理论、实验观察和潜在应用进行了综述。光子纳米喷射展现出理想特性的一种独特组合,包括沿多波长距离上路径的波传播(而不是倏逝波)、狭窄而潜在的亚波长束宽、高强度、波长灵敏度小以及纳米粒子和纳米凹陷引起的巨大背向散射扰动。因此,从超显微技术到光学数据存储、纳米图案化和生物光子学,光子纳米喷射对于推进当前纳米光子学技术具有相当大的前景。
Alexander Heifetz从伊利诺伊州埃文斯顿的西北大学于1999年获得应用数学学士学位(以优等成绩),2002年获得物理学硕士学位,2005年获得电子工程(光学)博士学位。他是西北大学Walter P. Murphy研究生奖学金的获得者。他博士论文的工作是全息光栅光衍射的信息存储和图像相关度的应用。他目前是美国癌症协会/金丝雀基金会的博士后研究员,在西北大学生物医学工程系工作。他的研究领域是生物医学应用的电磁散射理论与模拟。他最近的著作是关于利用米氏理论和时域有限差分法研究纳米粒子和生物细胞的光散射。
Soon-Cheol Kong分别于1995年、1997年和2003年从韩国首尔中央大学获得学士、硕士和博士学位。从2002年到2006年,他是韩国水原三星电子机械的高级研究员,从2004年到2005年,他是麻省理工学院的访问科学家。目前,他在西北大学担任博士后研究员。他的研究领域包括时域有限差分法、微波光子学、微/纳电磁学、天线在生物光子学中的应用、行波光电探测器、超高密度光存储、太阳能电池、生物检测和癌症早期检测。
Alan V. Sahakian从威斯康星大学麦迪逊分校获得了电子工程硕士学位、电子和计算机工程专业博士学位并辅修计算机科学。在研究生期间,他也是Medtronic公司的高级电气工程师。他在威斯康星大学帕克赛德分校获得了应用科学和物理学的学士学位。他目前是西北大学EECS和BME专业的教授和EECS大学本科课程项目的副主席。他也是EECS信号和系统部门主任和埃文斯顿医院学术机构的成员。他曾是空军技术学院可靠性和可维护性卓越中心的常驻访问学者。他是IEEE的会士。除了心电生理学,他的实验室还研究微波、毫米波和光子学方法的医学成像和诊断。他的研究由NSF(国家科学基金会)、国防部乳腺癌研究计划、国防情报局、爽健(Dr. Scholl)基金会和Medtronic公司资助。
Allen Taflove是美国伊利诺伊州埃文斯顿西北大学电子工程和计算机科学教授,自1971年以来,他一直帮助开创时域有限差分法(FDTD)的算法和应用。他的著作包括超过125篇期刊论文和《计算电动力学:时域有限差分法》的三个版本(1995年、2000年和2005年),该书已成为FDTD领域的标准参考书。他被科学信息研究所列为世界上被引用最多的技术作者之一。
Vadim Backman是西北大学McCormick工程与应用科学学院生物医学工程教授。他从哈佛大学和麻省理工学院获得了医学工程博士学位。他获得了许多荣誉,包括被《技术评论》杂志评选为全球前100名青年创新者之一和国家科学基金会职业奖。Backman博士的研究领域包括开发用于疾病的非侵入式筛查、诊断和检测的新颖生物光子学技术。研究的重点是纳米尺度、微观尺度和分子水平。
Z. G. Chen, A. Taflove, and V. Backman, Opt. Express 12, 1214 (2004).
X. Li, Z. Chen, A. Taflove, and V. Backman, Opt. Express 13, 526 (2005).
S. Lecler, Y. Takakura, and P. Meyrueis, Optics Lett. 30, 2641 (2005).
A. V. Itagi and W. A. Challener, J. Opt. Soc. America A 22, 2847 (2005).
Z. G. Chen, X. Li, A. Taflove, and V. Backman, Optics Lett. 31, 196 (2006).
A. Heifetz, K. Huang, A. V. Sahakian, X. Li, A. Taflove, and V. Backman, Appl. Phys. Lett. 89, 221118 (2006).
A. M. Kapitonov and V. N. Astratov, Optics Lett. 32, 409 (2007).
K. J. Yi, H. Wang, Y. F. Lu, and Z. Y. Yang, J. Applied Physics 101, 063528 (2007).
S. Lecler, S. Haacke, N. Lecong, O. Crégut, J.-L. Rehspringer, and C. Hirlimann, Opt. Express 15, 4935 (2007).
W. Wu, A. Katsnelson, O. G. Memis, and H. Mohseni, Nanotechnology 18, 485302 (2007).
A. Heifetz, J. J. Simpson, S.-C. Kong, A. Taflove, and V. Backman, Opt. Express 15, 17334 (2007).
M. Gerlach, Y. P. Rakovich, and J. F. Donegan, Opt. Express 15, 17343 (2007).
P. Ferrand, J. Wenger, A. Devilez, M. Pianta, B. Stout, N. Bonod, E. Popov, and H. Rigneault, Opt. Express 16, 6930 (2008).
S.-C. Kong, A. V. Sahakian, A. Heifetz, A. Taflove, and V. Backman, Appl. Phys. Lett. 92, 211102 (2008).
S. Yang and V. N. Astratov, Appl. Phys. Lett. 92, 261111 (2008).
E. McLeod and C. B. Arnold, Nature Nanotech. 3, 413 (2008).
Z. Chen, H. Chu, and S. Li, Optical metrology using a photonic nanojet, U.S. Patent 7,394,535 (2008).
X. Cui, D. Erni, and C. Hafner, Opt. Express 16, 13560 (2008).
S.-C. Kong, A. Sahakian, A. Taflove, and V. Backman, Opt. Express 16, 13713 (2008).
A. Devilez, B. Stout, N. Bonod, and E. Popov, Opt. Express 16, 14200 (2008).
A. Taflove and S. C. Hagness, Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd edn., Artech, Boston (2005).
C. L. Adler, J. A. Lock, B. R. Stone, and C. J. Garcia, J. Opt. Soc. America A 14, 1305 (1997).
J. A. Lock, C. L. Adler, and E. A. Hovenac, J. Opt. Soc. America A 17, 1846 (2000).
Y. L. Xu and R. T. Wang, Phys. Rev. E 58, 3931 (1998).
Online: http://www.astro.ufl.edu/∼xu/.
J. A. C. Veerman, A. J. H. Wachters, A. M. van der Lee, and H. P. Urbach, Opt. Express 15, 2075 (2007).
B. S. Luk’yanchuk, R. Paniagua-Domínguez, I. Minin, O. Minin and Z. Wang, Refractive index less than two: photonic nanojets yesterday, today and tomorrow, Optical Materials Express, 7(6):1820-1847, 2017 https://doi.org/10.1364/OME.7.001820I.
V. Minin, C.-Y. Liu, Y. E. Geints and O. V. Minin, Recent advances in integrated photonic jet-based photonics, Photonics, 7(2):41, 2020 http://dx.doi.org/10.3390/photonics7020041
A. J. Littlefield, J. Zhu, J. F. Messinger and L. L. Goddard, Photonic nanojets, Optics & Photonics News, 32(1):34–41, 2021 http://dx.doi.org/10.1364/OPN.32.1.00003
A. Darafsheh, Photonic nanojets and their applications, Journal of Physics: Photonics, 3(2):022001, 2021 https://doi.org/10.1088/2515-7647/abdb05


推荐两本FDTD的教材以纪念上月底去世的FDTD牛人 Allen Taflove教授。




