你的浏览器禁用了JavaScript, 请开启后刷新浏览器获得更好的体验!
输入关键字进行搜索
搜索:
数学底子较差,当初上学就学的不好,二十多年也忘的差不多了,只记得一点点微积分和线代。
是不是就从微积分和线代开始?后面 概率?数学分析?基础要了解的还有什么吗?
没有找到相关结果
粽子 - 我不是环但也有平凡的理想
赞同来自: 林威 、一块石头 、魏强 、Adele
哈哈哈我很想放一个@Vladimir的路径图呢。首先声明,学习路径是个很个人的事情。(当然这也意味着,大家容易有不同意见。我先抛砖引玉,还请友善交流)看看你喜欢什么方向咯。不算应用,数学大致可以分为代数和数论,几何和拓扑,当然还有分析类。当然也有很多其他分支,也有很多交叉性的东西。所以弄清楚自己对什么感兴趣是有很大帮助的。当然,怎么知道自己对什么感兴趣呢?好吧,你得先看看,学一点,接触接触。如果你喜欢微积分为代表的分析类,你可以去看菲赫金哥尔茨《微积分学教程》《普林斯顿微积分读本》,接下来学复分析,实分析。如果你喜欢代数类,你可以看丘维声或者蓝以中的《高等代数》(丘维声的视频真的很棒,这里推荐看视频而不是书,书贼厚),《Linea Algebra Done Right》(《线性代数应该这样学》)也是好书。(不过最好学过一些线性代数再看)。再往后你可以学习抽象代数,可以去看看群论彩图版,Artin的《代数》(纠正一下路径图,这本书有翻译),想要书薄一点可以用丘维声《抽象代数基础》。再往后就是交换代数,群表示论,李群李代数,同调代数,范畴论blabla……(好吧,越来越深了,后边的统统要求至少有点抽代基础)科普类的推荐《从一元一次方程到伽罗瓦理论》另一个有关系的方向是数论。不是很推荐潘承洞。因为他太喜欢“证明留给读者做练习”了= =,Rosen的《初等数论及其应用》不错。《现代数论经典引论》我也看过一点,上来就是主理想整环,(你自己看着办吧)。学完初等数论和抽象代数可以学代数数论,解析数论需要微积分。如果你喜欢几何与拓扑,可以尝试《Topology Without Tears》,剩下的看路径图吧,真的很详细了。(分析和几何路径图都是很详细,我就不再赘述)有些分支看起来似乎“高大上”,实则不需要太多前置知识,因为它们考验的主要是数学成熟度。比如抽象代数,比如拓扑学。虽然先学微积分可以帮助拓扑,线性代数可以辅助抽象代数,但跳过去直接学这两个也是可以的。除此之外我想介绍一些“冷门”分支。首先是图论。图论也是很有意思的一个分支,并且有许多部分不需要前置知识。我手里有一本沙特朗图论导引(好吧,几乎没看过)(其实我看过的图论是数竞小蓝本2333)然后是数理逻辑(尽管很冷门但对它感兴趣的人出乎意料地多)路径图有,汪芳庭也不错人教版教材中有许多没见过的选修课本。它们相当有意思且不会晦涩难懂。比如《对称与群》《矩阵与变换》《球面上的几何》《初等数论初步》《开关电路与布尔代数》等等(曾经上网课时候在人民教育出版社官网看到过。现在可能不容易再见到了吧)当然还有许多有意思的分支,以及许多与生活联系的部分,限于个人所见也就不再能够回答了。
中学物理初学者
林威 - 问之题,悟之理
1)数学分析I、高等代数I、解析几何2)数学分析II、高等代数II、常微分方程3)数学分析III、抽象代数、实变函数4)复变函数、偏微分方程、拓扑学5)概率论、数学模型、微分几何6)数理统计、应用随机过程、泛函分析、群论
其实成年人学数学,必须考虑是哪个方向,或者说,小目标是什么?按本科生教育的流程,很难扛下来。
要回复问题请先登录或注册
3 个回复
粽子 - 我不是环但也有平凡的理想
赞同来自: 林威 、一块石头 、魏强 、Adele
哈哈哈我很想放一个@Vladimir的路径图呢。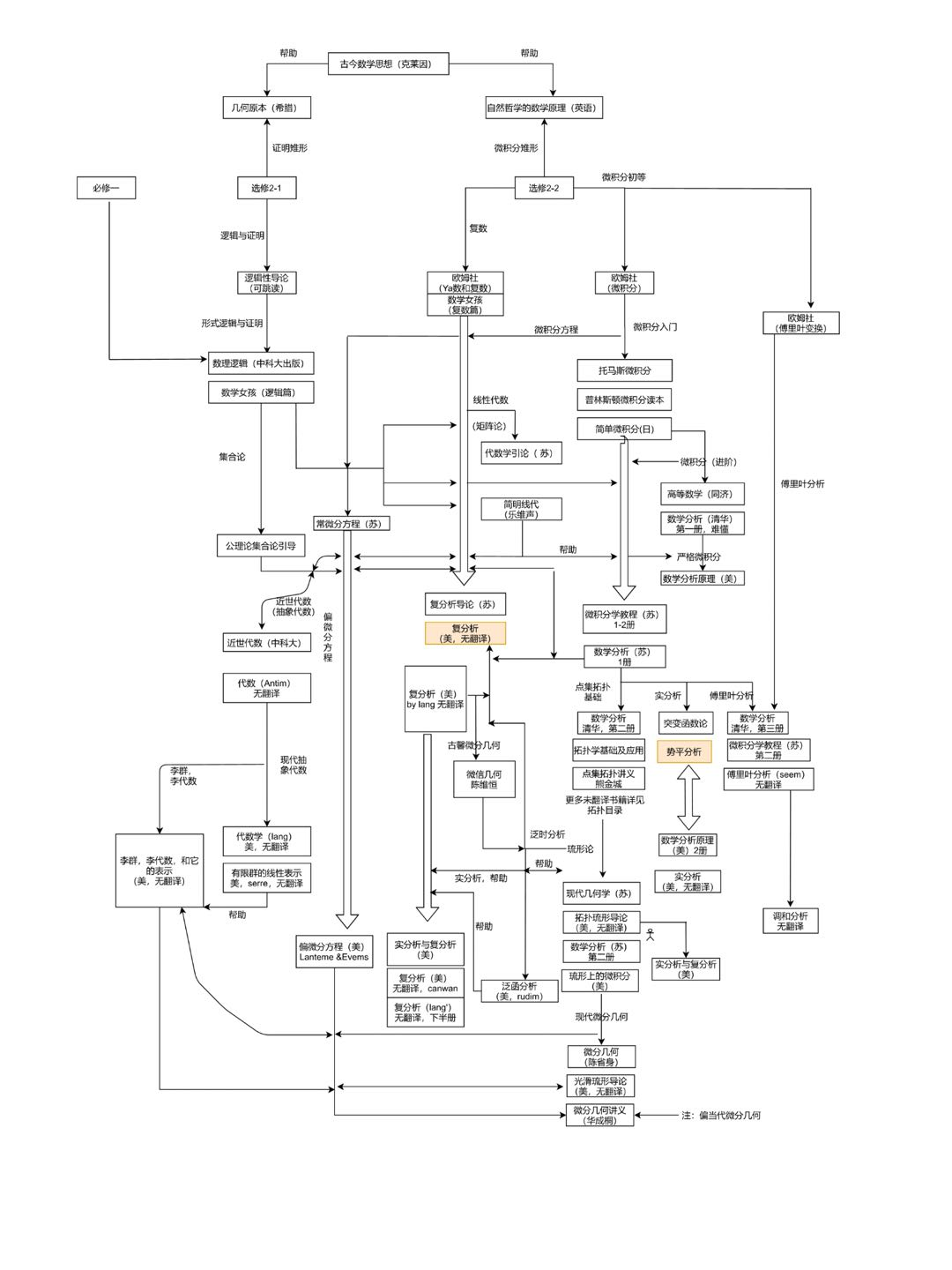
首先声明,学习路径是个很个人的事情。(当然这也意味着,大家容易有不同意见。我先抛砖引玉,还请友善交流)
看看你喜欢什么方向咯。不算应用,数学大致可以分为代数和数论,几何和拓扑,当然还有分析类。当然也有很多其他分支,也有很多交叉性的东西。所以弄清楚自己对什么感兴趣是有很大帮助的。当然,怎么知道自己对什么感兴趣呢?好吧,你得先看看,学一点,接触接触。
如果你喜欢微积分为代表的分析类,你可以去看菲赫金哥尔茨《微积分学教程》《普林斯顿微积分读本》,接下来学复分析,实分析。
如果你喜欢代数类,你可以看丘维声或者蓝以中的《高等代数》(丘维声的视频真的很棒,这里推荐看视频而不是书,书贼厚),《Linea Algebra Done Right》(《线性代数应该这样学》)也是好书。(不过最好学过一些线性代数再看)。再往后你可以学习抽象代数,可以去看看群论彩图版,Artin的《代数》(纠正一下路径图,这本书有翻译),想要书薄一点可以用丘维声《抽象代数基础》。再往后就是交换代数,群表示论,李群李代数,同调代数,范畴论blabla……(好吧,越来越深了,后边的统统要求至少有点抽代基础)科普类的推荐《从一元一次方程到伽罗瓦理论》
另一个有关系的方向是数论。不是很推荐潘承洞。因为他太喜欢“证明留给读者做练习”了= =,Rosen的《初等数论及其应用》不错。《现代数论经典引论》我也看过一点,上来就是主理想整环,(你自己看着办吧)。学完初等数论和抽象代数可以学代数数论,解析数论需要微积分。
如果你喜欢几何与拓扑,可以尝试《Topology Without Tears》,剩下的看路径图吧,真的很详细了。
(分析和几何路径图都是很详细,我就不再赘述)
有些分支看起来似乎“高大上”,实则不需要太多前置知识,因为它们考验的主要是数学成熟度。比如抽象代数,比如拓扑学。虽然先学微积分可以帮助拓扑,线性代数可以辅助抽象代数,但跳过去直接学这两个也是可以的。
除此之外我想介绍一些“冷门”分支。首先是图论。图论也是很有意思的一个分支,并且有许多部分不需要前置知识。我手里有一本沙特朗图论导引(好吧,几乎没看过)(其实我看过的图论是数竞小蓝本2333)
然后是数理逻辑(尽管很冷门但对它感兴趣的人出乎意料地多)路径图有,汪芳庭也不错
人教版教材中有许多没见过的选修课本。它们相当有意思且不会晦涩难懂。比如《对称与群》《矩阵与变换》《球面上的几何》《初等数论初步》《开关电路与布尔代数》等等(曾经上网课时候在人民教育出版社官网看到过。现在可能不容易再见到了吧)
当然还有许多有意思的分支,以及许多与生活联系的部分,限于个人所见也就不再能够回答了。
中学物理初学者
林威 - 问之题,悟之理
1)数学分析I、高等代数I、解析几何
2)数学分析II、高等代数II、常微分方程
3)数学分析III、抽象代数、实变函数
4)复变函数、偏微分方程、拓扑学
5)概率论、数学模型、微分几何
6)数理统计、应用随机过程、泛函分析、群论
其实成年人学数学,必须考虑是哪个方向,或者说,小目标是什么?按本科生教育的流程,很难扛下来。