自由粒子

首先考虑自由粒子，哈密顿量为

$$H=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}.$$

换成圆环坐标，即令$x=R\theta$，有

$$H=-\frac{\hbar^2}{2mR^2}\frac{d^2}{d\theta^2}.$$

此时其可以解释为以$I=mR^2$为转动惯量的平面转子，$L_z=-i\hbar\frac{d}{d\theta}$为垂直转动平面方向的角动量算符。（一个平移对称的问题转化成了一个旋转对称的问题）

本征能量$E$对应的解为：

$$\psi(\theta)=Ae^{in\theta}+Be^{-in\theta},$$

其中$n=\frac{2IE}{\hbar^2}$。由周期性边界条件$\psi(0)=\psi(2\pi)$，$n$必须为整数，这给出离散的能量谱：

$$E=\frac{n^2\hbar^2}{2I},\quad n\in\mathbb{Z}.$$

而归一化要求

$$|A|^2+|B|^2=\frac{1}{2\pi},$$

除此之外对系数没有更多的限制条件，这意味着任意满足上式的波函数$\psi_{(A,B)}$都是本征能量$E$对应的解，能量存在二重简并，这显然来自于一对动量大小相等左行/右行波（顺时针/逆时针转动）。$L_z$与哈密顿量对易，由于系统不存在其它对称性，它和哈密顿量的共同本征态是唯一确定的。

$L_z$的本征值和本征态容易求得，得到共同本征态和相应本征值：

$$
\begin{aligned}
\psi_n(\theta)&=\frac{1}{\sqrt{2\pi}}e^{in\theta},\\
E_n&=\frac{n^2\hbar^2}{2mR^2},\\
L_{z,n}&=n\hbar,
\end{aligned}
n=0,\pm 1,\pm 2,\ldots
$$

上述所有波函数的模方都是常函数$\frac{1}{\sqrt{2\pi}}$，这意味着（角）位置完全不确定，这正是（角）动量本征态应当具有的性质。

值得注意的是$n=0$的解$\psi_0(\theta)=\frac{1}{\sqrt{2\pi}}$是一个合法的归一化解，尽管它对应的能量为$0$。在如无限深势阱的问题中之所以要舍去零能解，是因为在那里零能波函数处处为零，而此处是一个可归一化的非零函数（得益于周期性边界条件）。物理上看，圆环零能解不仅位置概率密度是常函数，本身也是常函数，“不包含运动”（动量本征值为零），能量自然应该是零。

周期性的正则坐标，量子化的正则动量

注意到，虽然位置仍是连续变化的，但对应的动量却是离散的。做（离散）傅里叶变换，得到动量表象下的本征函数为：

$$
\begin{aligned}
\phi_n(l)&=\frac{1}{\sqrt{2\pi}}\int_0^{2\pi}\frac{1}{\sqrt{2\pi}}e^{in\theta}e^{-il\theta}d\theta\\
&=\delta_{nl}.
\end{aligned}
$$

即是说周期性的角位置，必然对应量子化的角动量。

环上粒子的能量本征值形式上和无限深势阱中的粒子很像，但性质大不相同。考虑如下叠加态：

$$\psi_1-\psi_{-1}\propto\sin(\theta),$$

其对应的动量波函数是两个尖峰的叠加$\delta_{1,l}-\delta_{-1,l}$，而无限深势阱的基态$\sin(\frac{n\pi x}{L})$对应的动量波函数是一个连续的分布（自行验证，连泡利也曾在这个问题上犯错）。

能量本征态的完备性

要证明能量本征态的完备性，即证明

$$\sum_{n=0,\pm 1,\ldots}|n\rangle\langle n|=\mathbb{1},$$

坐标表象下即

$$
\begin{aligned}
\sum_{n=0,\pm 1,\ldots}\langle\theta|n\rangle\langle n|\theta^{'}\rangle &=\delta(\theta-\theta^{'}),\\
\frac{1}{2\pi}\sum_{n=0,\pm 1,\ldots}e^{in(\theta-\theta^{'})}&=\delta(\theta-\theta^{'}),
\end{aligned}
$$

可以从复平面的几何图像上看出上式的成立性。

环上的$\delta$势

假设在$\theta=\pi$处存在一$\delta$势，$V(\theta)=\gamma\delta(\theta-\pi)$，我们沿用之前的方法求解该问题。

我们已经知道一维$\delta$势的通解为

$$
\begin{cases}
\psi(\theta)=Ae^{ik\theta}+Ce^{-ik\theta} & \theta < \pi,\\
\psi(\theta)=Be^{ik\theta}+De^{-ik\theta} & \theta > \pi,\\
\end{cases}
$$

由周期性边界条件，

$$
\begin{aligned}
A+C&=Be^{ik2\pi}+De^{-ik2\pi},\\
A-C&=Be^{ik2\pi}-De^{-ik2\pi},
\end{aligned}
$$

有$A=Be^{ik2\pi}$，$C=De^{-ik2\pi}$。由$\theta=\pi$处的连接条件，

$$
\begin{aligned}
Ae^{ik\pi}+Ce^{-ik\pi}&=Be^{ik\pi}+De^{-ik\pi},\\
Be^{ik\pi}-De^{-ik\pi}-Ae^{ik\pi}+Ce^{-ik\pi}&=\frac{2I\gamma}{\hbar^2}\left(Ae^{ik\pi}+Ce^{-ik\pi}\right),
\end{aligned}
$$

即

$$
\begin{aligned}
Be^{ik3\pi}+De^{-ik3\pi}&=Be^{ik\pi}+De^{-ik\pi},\\
Be^{ik\pi}-De^{-ik\pi}-Be^{ik3\pi}+De^{-ik3\pi}&=\frac{2I\gamma}{\hbar^2}\left(Be^{ik3\pi}+De^{-ik3\pi}\right),
\end{aligned}
$$

有

$$
\begin{aligned}
Be^{ik3\pi}+De^{-ik3\pi}&=Be^{ik\pi}+De^{-ik\pi},\\
De^{-ik3\pi}-De^{-ik\pi}&=\frac{I\gamma}{\hbar^2}\left(Be^{ik3\pi}+De^{-ik3\pi}\right),
\end{aligned}
$$

若$k\in\mathbb{Z}$，有$A=B=-C=-D$。得到全域上的归一化解

$$
\begin{aligned}
\psi_k(\theta)&=\frac{1}{2\sqrt{\pi}}\left(e^{ik\theta}-e^{-ik\theta}\right)\\
&=\frac{1}{\sqrt{\pi}}\sin(k\theta),
\end{aligned}
$$

其中忽略了一个整体相位因子$i$。由于$-k$和$k$对应的解只差一个整体相位因子（线性相关），以及解非零的要求，此处$k=1,2,\ldots$，不同于自由粒子。这组解对应的本征能量为

$$E_k=\frac{\hbar^2k^2}{2I},\quad k=1,2,\ldots$$

陈鄂生的《量子力学习题与解答》在求解初期就直接假设了$k$为整数，得到了上述的本征态。并且这组解的性质与$\delta$势的强度$\gamma$无关。然而，还存在其它的解。

若$k\notin\mathbb{Z}$，则

$$B=D\frac{e^{-ik\pi}-e^{-ik3\pi}}{e^{ik3\pi}-e^{ik\pi}},$$

耐心整理得到

$$\tan(k\pi)=\frac{iI\gamma}{\hbar^2},$$

上式要成立则左端为纯虚数，即$k$为纯虚数，令$k=i\kappa$，有

$$\tanh(\kappa\pi)=\frac{I\gamma}{\hbar^2},$$

$\tanh$函数的值域为$(-1,1)$，只要适当选取$\delta$势的强度$\gamma$就有对应$E < 0$的解

$$E_\kappa=-\frac{\hbar^2\kappa^2}{2I} < 0,\quad \gamma\in(-\frac{\hbar^2}{I},\frac{\hbar^2}{I}).$$

尽管并没有无穷远可供其波函数衰减至零，我们仍称其为束缚态，对应归一化波函数为

$$
\psi_\kappa(\theta)=\sqrt{\frac{2\kappa}{2\kappa\pi+\sinh(2\kappa\pi)}}
\begin{cases}
\cosh(\kappa\theta), & 0\leq\theta\leq\pi,\\
\cosh[\kappa(\theta-2\pi)], & \pi < \theta\leq 2\pi,
\end{cases}
$$

                

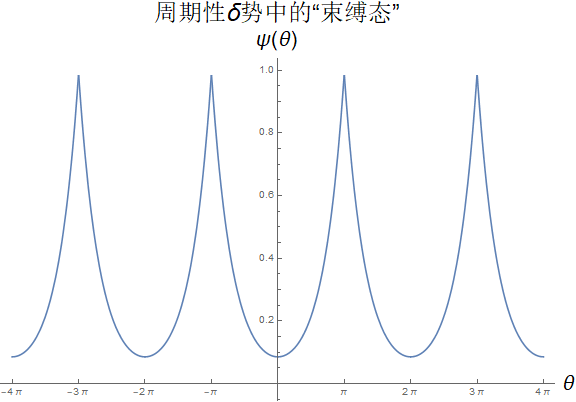
束缚态波函数图像如上图所示。

注意到该束缚态的存在与$\kappa$，进而与$\gamma$的正负无关，而只与$\gamma$的绝对值有关。这意味着在圆环上，即便是$\delta$势垒也可以存在束缚态！

束缚态的力学量分布

平均角位置为

$$
\begin{aligned}
\langle\theta\rangle&=\int_0^{2\pi}\theta\left|\psi(\theta)\right|^2d\theta\\
&=\frac{2\kappa}{2\kappa\pi+\sinh(2\kappa\pi)}\left(\int_0^\pi\theta\cosh^2(\kappa\theta)d\theta+\int_\pi^{2\pi}\theta\cosh^2[\kappa(\theta-2\pi)]d\theta\right)\\
&=\pi,
\end{aligned}
$$

这一结果是显然的。而平均角动量为

$$
\begin{aligned}
\langle p_\theta\rangle&=\int_0^{2\pi}\psi^*(\theta)(-i\hbar\frac{d}{d\theta})\psi(\theta)d\theta\\
&=-\frac{i\hbar\kappa^2}{2\kappa\pi+\sinh(2\kappa\pi)}\left(\int_0^\pi\sinh(2\kappa\theta)d\theta+\int_\pi^{2\pi}\sinh[2\kappa(\theta-2\pi)]d\theta\right)\\
&=0,
\end{aligned}
$$

可见，其确实具有束缚态的特征。

角位置不确定性为

$$
\begin{aligned}
\sigma_\theta&=\sqrt{\langle\theta^2\rangle-\pi^2}\\
&=\sqrt{\frac{1}{2\kappa^2}+\frac{2\pi(\kappa^2\pi^2-3)}{3\kappa[2\kappa\pi+\sinh(2\kappa\pi)]}}
\end{aligned}
$$

角动量不确定性为

$$
\begin{aligned}
\sigma_{p_\theta}&=\sqrt{\langle p_\theta^2\rangle-0}\\
&=\sqrt{-\frac{2\hbar^2\kappa^3}{2\kappa\pi+\sinh(2\kappa\pi)}\left(\int_0^\pi\cosh^2(\kappa\theta)d\theta+\int_\pi^{2\pi}\cosh^2[\kappa(\theta-2\pi)]d\theta\right)}\\
&=\sqrt{-\hbar^2\kappa^2}???
\end{aligned}
$$

像普通的一维$\delta$势中一样，我们又一次遭遇了二阶导数发散带来的问题。补充$\theta=\pi$处发散项的贡献，有

$$
\begin{aligned}
\sigma_{p_\theta}^2&=\langle p_\theta^2\rangle-0\\
&=-\frac{2\hbar^2\kappa^3}{2\kappa\pi+\sinh(2\kappa\pi)}\left(\int_0^\pi\cosh^2(\kappa\theta)d\theta+\int_\pi^{2\pi}\cosh^2[\kappa(\theta-2\pi)]d\theta\right)\\
&+\frac{4\hbar^2\kappa^2}{2\kappa\pi+\sinh(2\kappa\pi)}\int_{\pi^-}^{\pi^+}\cosh(\kappa\theta)\sinh(\kappa\theta)\delta(\theta-\pi)d\theta\\
&=\hbar^2\kappa^2\left(1-\frac{4\kappa\pi}{2\kappa\pi+\sinh(2\kappa\pi)}\right)\geq 0
\end{aligned}
$$

$\sigma_\theta\sigma_{p_\theta}=$