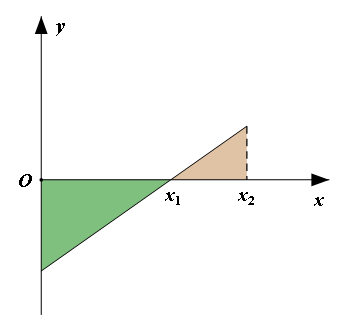“典例问答”栏目将不定期剖析典型问题，把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”，我将持续分享高中物理的干货哟。
问：高中物理有那么多种图像，该如何看呢？难道是趴窗户看？亦或是45度角仰天看？
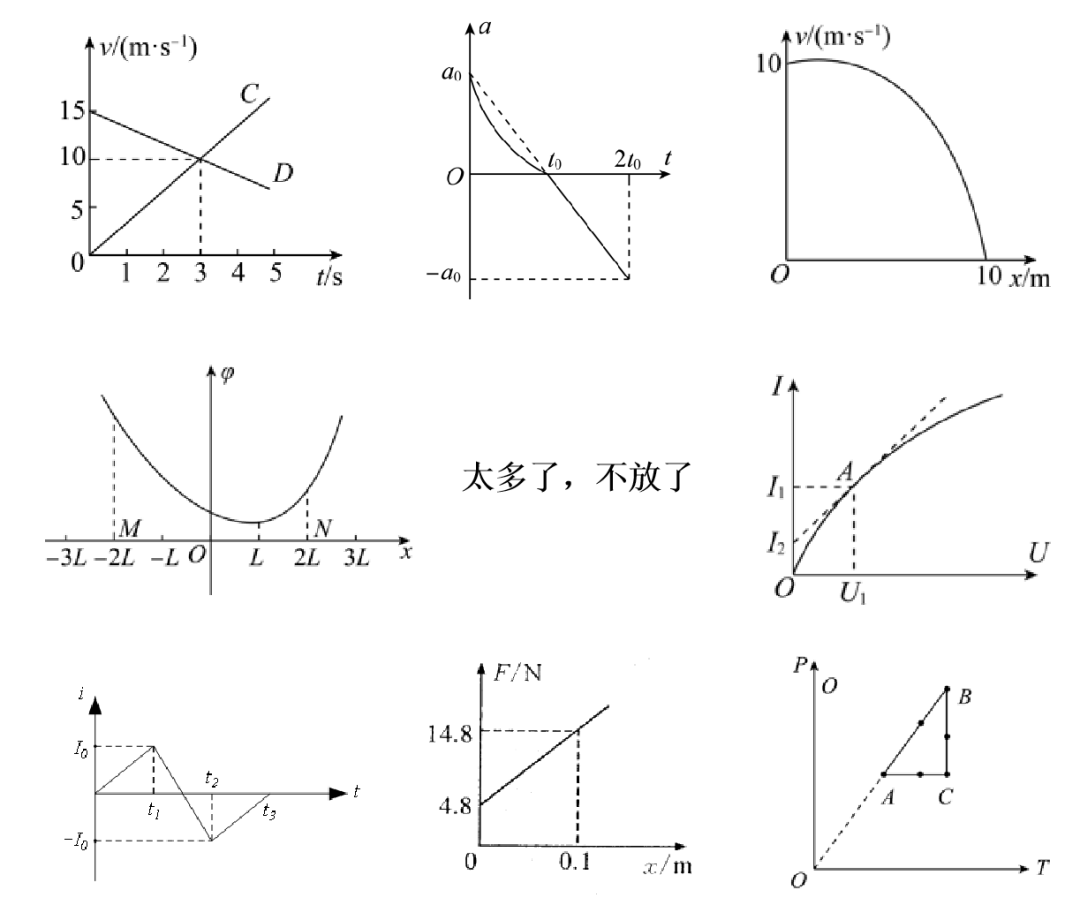
问题里的困惑不在于图像种类多，而是在于挖掘图像信息时有没有确定的方法。咱总不能把每类图像的特点当做结论给背下来吧？愚公移山的精神咱可以发扬，但是有飞机大炮就别用小米步枪了，不是吗？其实不论什么样的图像，挖掘其信息的角度一共就那么几个，咱这就一一说来。
图线上的点
无论图像中的图线是什么形状，线都是由点构成的，把点的含义弄清楚是先决条件。在平面直角坐标系里，一个点用坐标（x，y）来表示。至于x和y分别表示什么意义，那就要看坐标轴代表什么物理量了。所以请一定要牢记——看图先看坐标轴！
比如常见的x-t图，反映的就是t时刻物体的位置坐标是x。v-t图反映的就是t时刻物体的速度为v。U-I图反映的就是导体中的电流为I时对应的导体两端的电压为U。
对于很多是矢量的物理量而言，其方向特点是不能忽视的。如果这个矢量的方向只有两种可能（比如向左和向右），那么这个矢量可以用其数值前的正负号来体现它的方向。如此，坐标的取值既能反映出这个矢量的大小（坐标值的绝对值），又能反映出这个矢量的方向（坐标值的符号）。比如物体做直线运动时，描述物体运动规律的x-t图和v-t图，纵轴分别表示位置x和速度v。x-t图中的点就能反映出某个时刻物体的位置大小和方向；v-t图中的点就能反映出某个时刻物体的速度大小和方向。另外，对于点而言，交点往往有一些特殊的含义。比如截距，它是图线与坐标轴的交点坐标。显然这个坐标里起码有一个坐标值为0，这往往是个特殊状态。再比如说图线的交点，意味着两条图线都会出现这个状态。
所以嘛，在x-t图像中，两条图线的交点意味着两个物体运动时，同一时刻出现在了同一位置，这不就是相遇了么？而在v-t图中，两条图线的交点意味着两个物体运动时，同一时刻两个物体的速度相同。当把坐标轴所代表的物理量换掉，点的物理意义就会发生改变。但是读取它的信息也不难嘛，不是吗？开头的九宫图拿去练手，不谢。
图线的形状
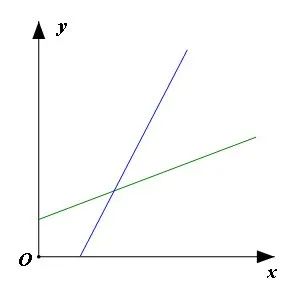
对于直线来说，咱就只考虑倾斜这种一般情形吧(直线与坐标轴平行视为特殊情况)。然而倾斜是有差别的，体现这个差别的就是倾斜程度——斜率。什么是斜率呢？也就是在倾斜直线上任取两点，这两点的纵坐标差值 与横坐标差值 的比值，即斜率k为： 下图中选取了相同的 值，显然蓝色图线上对应的 值要大一些。根据斜率的定义可知，蓝色图线的斜率更大，意味着蓝色图线更倾斜。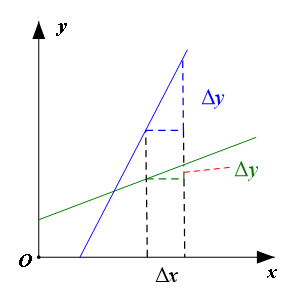
如果坐标轴x、y代表的物理量使得 有对应的物理意义，那么这条图线的斜率肯定要被我们关注呀！比如x-t图的图线斜率，v-t图的图线斜率，F-m图的图线斜率，等等。明白了直线情形，曲线情形也就很容易掌握了。在物理学里面有个说法叫“化曲为直”，也就是极限的思想！
曲线的特点无非就是弯曲的方向不同、弯曲的程度不同。弯曲的方向可以通过曲线上点的取值反映出来，而弯曲的程度依旧是用斜率来反映。和直线情形一样，也要在曲线上任取两点，求出这两点的纵坐标差值 与横坐标差值 的比值。只不过曲线和直线不同的地方就在于，直线上任取两点求得的 值都是一样的，而曲线上任取两点求得的 值就不一定相同了。所以对于曲线来说，逐个位置判断该处的斜率才有意义。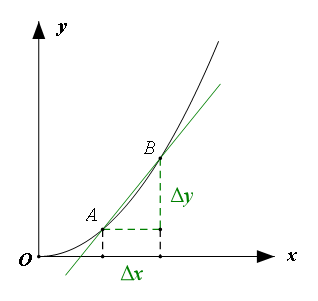
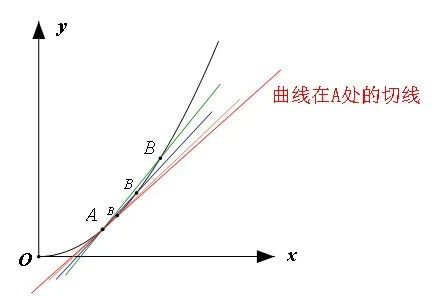
怎样才能做到逐个位置判断呢？比如我想判断上图中A点处曲线的弯曲程度，那我就应该在曲线上另取一点B，用直线AB的斜率来表示A点处曲线的弯曲程度。显然直线AB的斜率与A点处曲线的真实弯曲程度是有差异的。我们必须想办法缩小这个差异，直到两者相差无穷小！诺，上面的地球美景不是白给你看的，是让你去迁移思考的
。这就要求B无限地靠近A，只有这样，由A、B两点求出的 的极限值才是A点处曲线的弯曲程度。由于A、B无限的靠近，极限情形下直线AB就变成了在A点处曲线的切线！由此就能得到结论——曲线上某处的切线斜率反映的就是曲线在该处的弯曲程度。
现在咱就可以统一的来看待斜率了——如果坐标轴x、y代表的物理量使得 有对应的物理意义，无论图线是直线还是曲线，都是关注图线在该处的切线斜率！！！只不过对于直线图线来说，这条切线就是它自己本尊而已；而对于曲线图线来说，我们就要着重强调切线这个对象了。至于这个斜率表示速度、加速度、电场强度、电动势.....看图先看坐标轴的咒语念起来吧！
面积
这里提到的面积指的是一段图线的下方与坐标轴围成的图形面积。它反映了横、纵坐标x、y的乘积。对于图线是平行于横轴的情形，咱可以很容易求出这个面积的大小就等于 。
如果图线是倾斜直线或者曲线，咱也只需要用极限的思想处理就行——把这段图线分割成很多小段，每一小段图线就可以近似地看成是平行于坐标轴的线段。那么这一小段图线与坐标轴围成的图形面积不就是对应的 么？最后把这些所有小段的 求和，极限情形下的结果就是图线与坐标轴所围成的图形面积啦。显然，这个面积依然反映了横纵坐标x、y的乘积。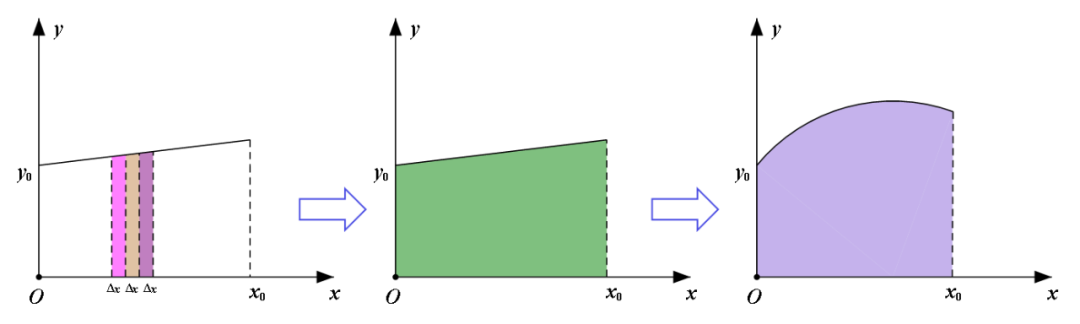
如果坐标轴代表的物理量之间的乘积有确定的物理意义，那么图线和坐标轴围成的面积就是咱需要关注的。比如v-t图像，图线与坐标轴所围成的图形面积表示的就是位移。同理，F-t图像中，图线与坐标轴所围成的图形面积表示的就是力F的冲量。I-t图像中，图线与坐标轴所围成的图形面积表示的就是电量。这里有个细节需要注意。前文里提到点的意义时，对于一维矢量来说，其值的正负号用来表示这个矢量的方向。那么当图线出现在坐标轴的正负两侧时，其与坐标轴所围成的图形面积虽然只有大小，但如果这个面积对应的物理量也是矢量的话，咱就可以给这个面积前面加上符号，从而能够反映出这个矢量结果的方向特点！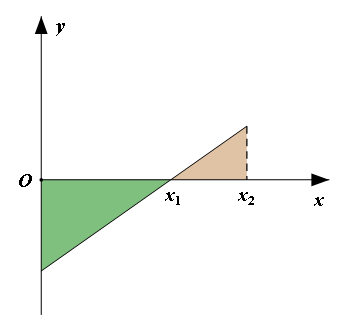
怎么样，对于一个具体的物理图像而言，点、线、面的含义不就显而易见了么？
虽然图像的图形有各种各样，但是我们还是最喜欢直线的图形。为啥？简单呗！在探究两个变量y与x的关系时，如果得到的图像是一条直线，咱就可以马上回答：y与x之间是一次函数的关系，也就是咱熟悉的表达式——y=kx+b。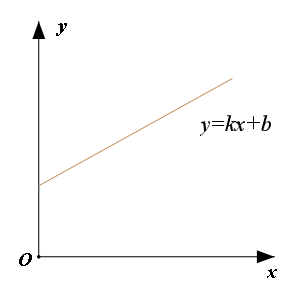
那如果得到的图线不是直线咋办？咱可以尝试着把坐标轴变换一下！比如图像看起来像抛物线，即y与x之间可能满足关系式 。如果现在用一个新的变量z代替 ，那么关系式就变成了y=kz。显然y就是z的一次函数，在y、z构成的平面直角坐标系里，图线就是一条直线！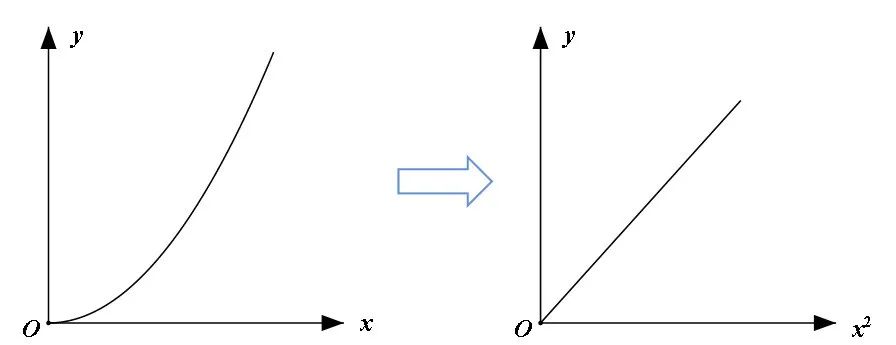
如此就能根据y、z图像中的数据找出y与z的定量关系，然后再把z换成 ，这不就间接得到了y与x的关系了么？所谓曲线救国也不过如此嘛。类似的做法，假若y与x成反比，即 ，也可以把坐标轴进行简单的变换，从而得到一条倾斜直线的图像。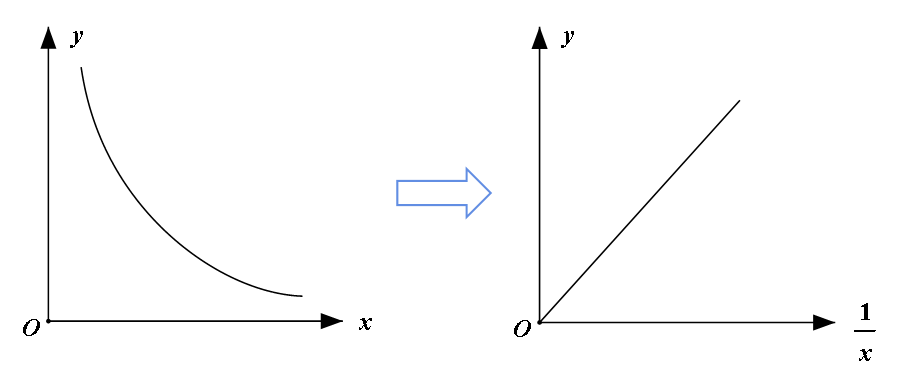
再比如著名的开普勒第三定律，即行星绕太阳运转的椭圆轨道的半长轴a的立方与其运转周期T的平方比值为一常数。写成等式为： 天文数字可都是很大的，数学上的对数运算就是为此而生的。如果你已经知道了这条著名的定律，现在让你通过一些观测数据来验证它，有啥好法子没？你愿意直接把轨道半长轴的立方算出来、把公转周期的平方算出来吗？要不这办法还是留给你来吧。我想的是把等式两边同时取对数！来看看效果吧。 接下来，横纵坐标怎么取，心里有数了么？以上就是挖掘图像信息的全部角度。你抓住了这些图像的本质规律后，面对形形色色的物理图像，你还会觉得上帝在你眼前遮住了帘，忘了掀开吗？
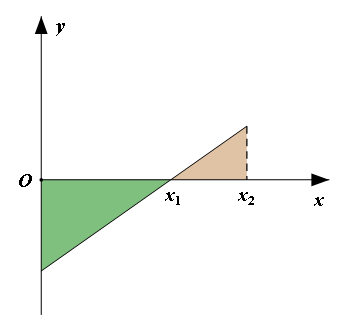
