“典例问答”栏目将不定期剖析典型问题,把最本质的方法与规律呈现给读者。欢迎大家关注“因物悦理”,我将持续分享高中物理的干货哟。

问:力的分解具有任意性,为啥又要沿力的效果分解呢?

力的分解与力的合成一样,都是根据平行四边形定则来进行的。所以单纯讨论力的分解其实就是一个数学问题——即找出合适的平行四边形就完事了。虽说数理不分家,但是亲兄弟也得明算账。如果你考虑具体的物理问题,力的分解与合成它可是有着浓厚的物理学思想——等效替代!所以,当咱们对具体物理问题里的力进行分解时,必然得按照实际的作用效果来寻找力的替代者。作为一个数学问题来说,力的分解有着坚实的数学依据——即平面(空间)向量的基本定理。这里咱们就只讨论简单的平面向量。力是矢量,即高中数学里说的向量,其基本定理为平面内任意一个向量能够被这个平面里两个不共线的向量给唯一表示出来。这两个不共线的向量称为基向量,其可以任意选取的,只要两者不共线就行。
正是由于这个原因,所以力的分解确实可以说是任意的,大爷想怎么来就怎么来。但是一旦加上了物理背景,这组基向量就必须得老老实实地按照实际效果来确定了。毕竟找出物理现象的背后原因是物理学的本分,无论是运动状态的改变也好、物体的形变也罢,都是力对物体产生的效果。所以面对一个个具体的物理问题,你不按照力的实际效果去分解,那些其它的分解结果也毫无实际意义呀。这就好比我只需正确地写出“茴香豆”的简体中文,你却告诉我“茴”字有好多种写法,这就很令人无语了不是?
除了以上两种情形容易产生困惑之外,其实还有一种情形也会令初学者头疼不已,看看下图是不是会让你想退出这篇文章呢?千万不要手抖退出哟,好戏还在后头呢。
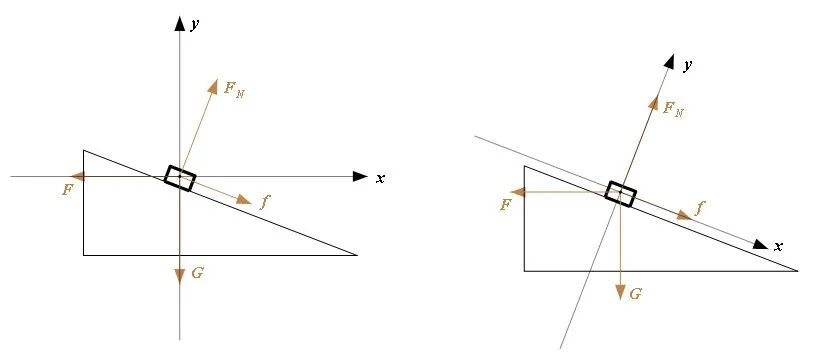
无论物体是平衡状态还是非平衡状态,求解多个力的合力时,正交分解法必定是永远滴神。那么问题来了,为啥正交分解就是香?正交的方向能任意选?有啥挑选的良方能悄悄透露一下吗?不急不急,排排坐,一个一个来回答。
首先要强调一点:正交分解法的全称是正交分解合成法,落脚点是合成!也就是把力先分解再合成,颇有一番退一步海阔天空的味道。既然如此,此法其实就是一个纯粹的数学方法,其严格的理论依据自然是上面提到的向量基本定理啦。
那为啥要特意强调正交呢?正交指的是你选择的两个基向量是互相垂直的,这意味着它俩彼此独立。如此一来,向量以此为基准进行分解之后,其分量就不会彼此干扰,后续求解时会方便很多。体会不到单身独立的自由?举个例子,同样是二元一次方程组,你是喜欢第一类的方程还是第二类的方程呢?

显然是第一类方程更容易撒。每个方程都只含有一个独立的未知数,解起来就是简单的一元一次方程。要是像第二类方程,每个未知数之间彼此都有关联,解起来是不是要麻烦一些?解方程的时候咱可不喜欢未知数之间你是风儿我是沙,不要这种缠绵的哈。至于正交的方向能不能任意选,这还用说么?肯定可以!毕竟此法只是一个单纯的数学方法而已,而且其落脚点是求合力,哪用得着去管每个力的分力的效果呢?而且求合力与力的分解不同,其结果是唯一的。所以不管你怎么选取两个正交的方向,结果都是一样的,别以为穿上马甲就认不出你了!
虽然正交的方向可以任意选取,不过对于具体问题来说,选择特定的方向会使得后续的求解相对简洁。这里的选择并没有统一的标准,只能具体问题具体分析。比如尽量使得更多的力与正交方向重合,这样可以少分解一些力。但是这个标准在前面给出的斜面图例中就用不上。再比如说,为了使得方程组里的未知数尽量彼此独立,咱们一般不去分解滑动摩擦力,即选择沿滑动摩擦力方向和垂直滑动摩擦力方向去选择正交方向。因为根据滑动摩擦力的特点有 ,要是把滑动摩擦力和压力分解了,方程解起来会麻烦许多。不信你就去试试。还有,如果物体处于非平衡状态,分解方向是不是一定要沿着加速度方向和垂直加速度方向呢?这也不能一概而论。但凡需要具体问题具体分析的情形,你就该亲自动手试试。方法可以传授,但是经验只能靠自己在实践中加以积累。